Om de regels voor de spelling van werkwoorden goed

Naam: …………………..
Datum: ………………………..
_________________________________________________________________
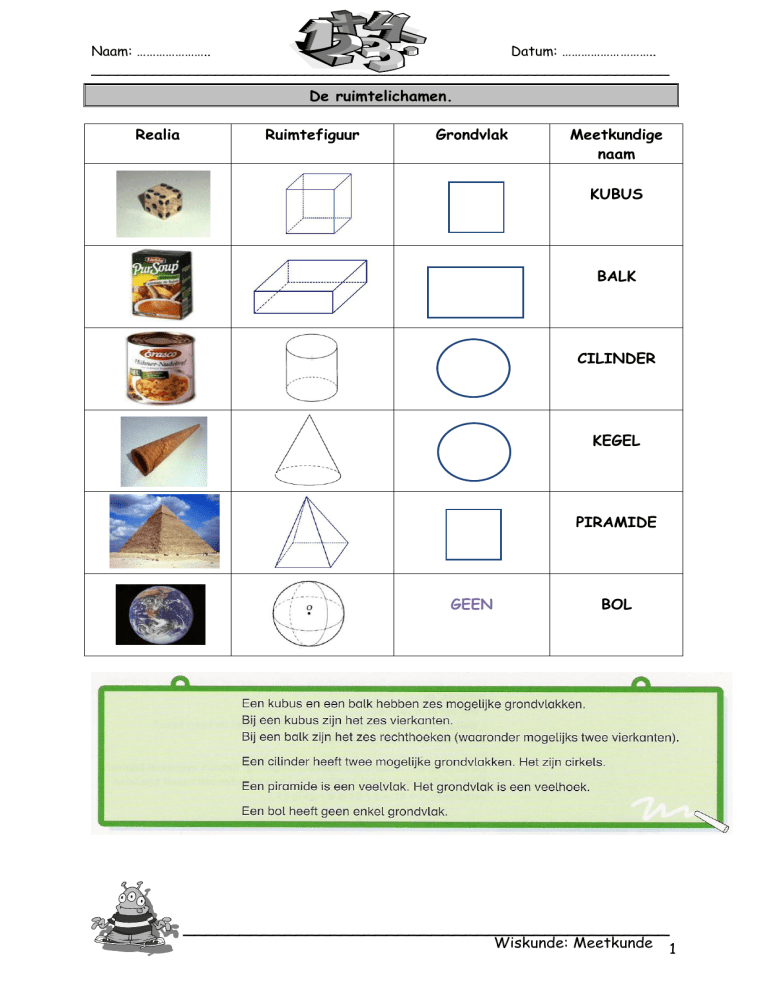
De ruimtelichamen.
Realia
Ruimtefiguur
Grondvlak
Meetkundige
naam
KUBUS
BALK
CILINDER
KEGEL
PIRAMIDE
GEEN
BOL
___________________________________________
Wiskunde: Meetkunde
1
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Vlakke figuren: veelhoeken, regelmatige veelhoeken, veelhoeken
ingeschreven in cirkels
Het begrip regelmatige veelhoek:
___________________________________________
Wiskunde: Meetkunde 2
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
De cirkel:
De Regelmatige ingeschreven veelhoeken tekenen:
De regelmatige ingeschreven vierhoek:
Werkwijze :

Teken een cirkel. Duid het middelpunt aan.

Teken de diameter [AB].

Teken ook de diameter [CD]. Let erop dat hij loodrecht op diameter [AB] staat.

Je verkrijgt een regelmatige vierhoek.

Controleer. Zijn de hoeken even groot ? (ja – 90°) Zijn de zijden even lang ?
(nameten)
___________________________________________
Wiskunde: Meetkunde 3
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
De regelmatige ingeschreven achthoek:
Hoe kan je, vertrekkende van een regelmatige ingeschreven vierhoek, een regelmatige
ingeschreven achthoek tekenen ?
Werkwijze :

Teken een regelmatige vierhoek.

Halveer de zijden.

Trek een symmetrieas door het midden van de zijden en door het middelpunt.

Waar de symmetrieassen de cirkelomtrek raken krijg je de vier bijkomende
hoekpunten.
___________________________________________
Wiskunde: Meetkunde 4
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
De regelmatige ingeschreven driehoek:
Werkwijze :

Teken een cirkel. Duid het middelpunt aan.

Teken de diameter/middellijn [MN].

Trek vanuit M twee boogjes met de passer op de cirkelomtrek. De passeropening
is even lang als de straal. Je hebt nu twee snijpunten: R en S.

Verbind R met S
zijde [RS].

Teken ook de zijden [NR] en [NS].

Je hebt nu de regelmatige (gelijkzijdige) driehoek RNS.

Controleer. Zijn de hoeken even groot ? (ja – 60°) Zijn de zijden even lang ?
(nameten)
___________________________________________
Wiskunde: Meetkunde 5
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
De regelmatige ingeschreven zeshoek:
Werkwijze :

Teken een cirkel. Duid het middelpunt aan.

Teken de diameter/middellijn [VW].

Trek vanuit V twee boogjes met de passer op de cirkelomtrek. De passeropening
is even lang als de straal. Je hebt nu twee snijpunten: X en Y.

Trek vanuit W twee boogjes met de passer op de cirkelomtrek. De passeropening
is even lang als de straal. Je hebt nu twee snijpunten: Z en U.

Verbind de opeenvolgende snijpunten.

Je hebt nu de regelmatigezeshoek (VYUWZX)

Controleer. Zijn de hoeken even groot ? (ja – 120°) Zijn de zijden even lang ?
(nameten)
___________________________________________
Wiskunde: Meetkunde 6
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Opdracht 1:



Teken een cirkel met straal 5cm.
Teken een ingeschreven regelmatige vierhoek. A B C D
Teken vanuit de ingeschreven regelmatige vierhoek een regelmatige ingeschreven
achthoek. A E B F C G D H
Opdracht2:



Teken een cirkel met straal 4cm.
Teken een ingeschreven regelmatige driehoek. K L M
Teken vanuit de ingeschreven regelmatige driehoek een regelmatige ingeschreven
zeshoek. K N L O M P
___________________________________________
Wiskunde: Meetkunde 7
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Rubriceren van de driehoeken.
1. Rubriceren naar de zijden:
omschrijving
naam
Een driehoek met drie
gelijke zijden.
Gelijkzijdige driehoek
figuur
(de drie hoeken zijn gelijk : 60°)
Een driehoek met ten
minste twee gelijke zijden
Gelijkbenige driehoek
( de twee basiszijden zijn gelijk)
Een driehoek met drie
verschillende zijden
Ongelijkzijdige driehoek
Opmerking :
 Iedere gelijkzijdige driehoek is gelijkbenig, maar niet iedere gelijkbenige
driehoek is gelijkzijdig !
2. Rubriceren naar de hoeken:
omschrijving
naam
Een driehoek met drie
scherpe hoeken
( < 90°)
Scherphoekige driehoek
Een driehoek met twee
scherpe hoeken en één
rechte hoek
( = 90° )
Een driehoek met twee
scherpe hoeken en één
stompe hoek
(> 90° en < 180° )
figuur
Rechthoekige driehoek
Stomphoekige driehoek
Opmerking :
 Elke driehoek heeft twee scherpe hoeken. De derde hoek bepaalt de naam.
 De som van de hoeken van een driehoek is altijd 180°.
___________________________________________
Wiskunde: Meetkunde 8
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
3. Rubriceren naar de zijden en de hoeken:
naam
figuur
Een gelijkbenige rechthoekige driehoek
Een ongelijkzijdige rechthoekige driehoek
Een gelijkbenige stomphoekige driehoek
Een ongelijkzijdige stomphoekige driehoek
Een gelijkbenige scherphoekige driehoek
Een ongelijkzijdige scherphoekige driehoek
Een gelijkzijdige scherphoekige driehoek
___________________________________________
Wiskunde: Meetkunde 9
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Rubriceren in de verzameling van de ruimtelichamen.
De verzameling der lichamen eens aandachtig bekeken.
Waar zouden we naar kunnen kijken om onderstaande lichamen te ordenen ?
…………………………………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………………………………
We maken de volgende afspraak:
We maken een deelverzameling van lichamen die volledig begrensd zijn door veelhoeken.
Wat is een veelhoek ?
…………………………………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………………………………
___________________________________________
Wiskunde: Meetkunde 10
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Vul onderstaand venn-diagram in met de nummers van de lichamen op het vorige blad.
L = { de lichamen }
V = { de veelvlakken }
W = { de niet-veelvlakken }
Besluit:
Een lichaam is een veelvlak als
…………………………………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………………………………
Een lichaam is een niet-veelvlak als
…………………………………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………………………………
___________________________________________
Wiskunde: Meetkunde 11
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Rubriceren in de verzameling van de ruimtelichamen.
Indeling volgens de zijvlakken:
Rangschik de lichamen als volgt:
V = { de veelvlakken }
A = { de veelvlakken begrensd door juist 4 zijvlakken }
B = { de veelvlakken begrensd door juist 5 zijvlakken }
C = { de veelvlakken begrensd door juist 6 zijvlakken }
D = { de veelvlakken begrensd door meer dan 6 zijvlakken }
A = { de viervlakken }
B = { de vijfvlakken }
C = { de zesvlakken }
We verkennen de verzameling van de zesvlakken.
We kijken naar de soorten veelhoeken van de zijvlakken.
 Een zesvlak dat volledig wordt begrensd door vierkanten noemen we
een kubus.
Voorbeeld: nr. ………………..
 Een zesvlak dat volledig wordt begrensd door parallellogrammen noemen we
een parallellepipedum.
Voorbeeld: nr. ………………..

Een zesvlak dat volledig wordt begrensd door rechthoeken noemen we
een balk.
Voorbeeld: nr. ………………..
___________________________________________
Wiskunde: Meetkunde 12
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Eigenschappen van de vierhoeken.
Het trapezium:
 Een trapezium is een vierhoek met minstens één paar
evenwijdige zijden.
 De diagonalen zijn ongelijk.
Het parallellogram:
 Een parallellogram is een trapezium met twee paar
evenwijdige zijden.
 In een parallellogram zijn de overstaande
zijden gelijk en evenwijdig.
 In een parallellogram zijn de overstaande hoeken gelijk.
 De diagonalen zijn ongelijk (uitgezonderd als het een rechthoek is) en
halveren elkaar, maar staan niet loodrecht op elkaar (uitgezonderd als het
een ruit is).
De rechthoek:
 Een rechthoek is een parallellogram met rechte
hoeken.
 In een rechthoek zijn de overstaande zijden
gelijk en evenwijdig.
 In een rechthoek zijn de vier hoeken recht.
 De diagonalen zijn gelijk en halveren elkaar, maar staan niet loodrecht op
elkaar.
De ruit:
 Een ruit is een parallellogram met gelijke zijden.
 In een ruit zijn de vier zijden gelijk en de
overstaande zijden zijn evenwijdig.
 De overstaande hoeken zijn gelijk.
 De diagonalen zijn ongelijk en halveren elkaar, maar
staan loodrecht op elkaar.
Het vierkant:
 Een vierkant is een ruit met rechte hoeken.
 In een vierkant zijn de vier zijden gelijk en de
overstaande zijden zijn evenwijdig.
 De vier hoeken zijn recht.
 De diagonalen zijn gelijk en halveren elkaar en staan
loodrecht op elkaar.
___________________________________________
Wiskunde: Meetkunde 13
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Opdracht 1 : Spiegelingen.
1. Er zijn telkens twee vlakke figuren gegeven. Zijn de figuren gespiegeld ten opzichte
van elkaar ? Noteer ja of neen bij de figuren.
Indien ja , teken dan de spiegel (= symmetrieas ).
___________________________________________
Wiskunde: Meetkunde 14
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Opdracht 2 : Spiegelingen.
2. Teken de corresponderende spiegelfiguur.
___________________________________________
Wiskunde: Meetkunde 15
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
De schijf en haar delen.
Om te onthouden:
o = het middelpunt:
r = de straal:
Het vaste punt noemt men het middelpunt van de schijf.
Het is overal even ver van de schijfomtrek verwijderd.
(als je een passer gebruikt om een cirkel te tekenen is dit
het punt waar de passer om zijn as draait.)
Een lijnstuk van het middelpunt naar de schijfomtrek.
Je kan oneindig veel stralen tekenen. Alle stralen zijn even lang.
d = de diameter :
Een lijnstuk dat twee punten van de cirkel verbindt en die
door het middelpunt snijdt.
Je kan oneindig veel diameters tekenen. Alle diameters zijn
even lang.
Een diameter = 2 X de straal
k = koorde :
b = boog :
Een koorde is een lijnstuk die twee willekeurige punten van de
cirkel verbindt.
Dit is het deel dat wordt afgesneden van de cirkel door een koorde.
Omtrek =
x d
=x 2 x r
___________________________________________
Wiskunde: Meetkunde 16
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
= 3,14 x 2 x r
Het middelpunt van een schijf bepalen.
Om te onthouden:
Hoe zoek je het middelpunt van de schijf wanneer dit niet gegeven is ?
1.
2.
3.
4.
teken een koorde in de schijf.
zoek het midden van de koorde.
Teken door het midden van de koorde een loodrechte lijn door de schijf.
Het midden van dit lijnstuk is het middelpunt.
___________________________________________
Wiskunde: Meetkunde 17
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Eigenschappen van de diagonalen in de vierhoeken.
___________________________________________
Wiskunde: Meetkunde 18
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Eigenschappen van de diagonalen in de vierhoeken.
Welke in onderstaande figuren zijn diagonalen ?
Overtrek ze in het groen.
In een vierhoek verbindt een diagonaal de
overstaande hoekpunten.
___________________________________________
Wiskunde: Meetkunde 19
Naam: …………………..
Datum: ………………………..
_________________________________________________________________
Eigenschappen van de diagonalen in de vierhoeken.
Trek in de gegeven vierhoeken de diagonalen met groen.
___________________________________________
Wiskunde: Meetkunde 20