Bank H17 VWO Pythagoras

De Wageningse Methode
1
2
OpgavenBank H17 VWO Pythagoras
Gianni gaat een penalty (strafschop) nemen. Hij legt
de bal op de penaltystip: 11 meter, midden voor het
doel. Het doel is 8 meter breed en 3 meter hoog.
Gianni schiet genadeloos hard, maar helaas precies
tegen de kruising van paal en lat: geen doelpunt
dus.
Nemen aan dat de baan die de bal beschrijft recht
is.
Bereken de lengte van de baan.
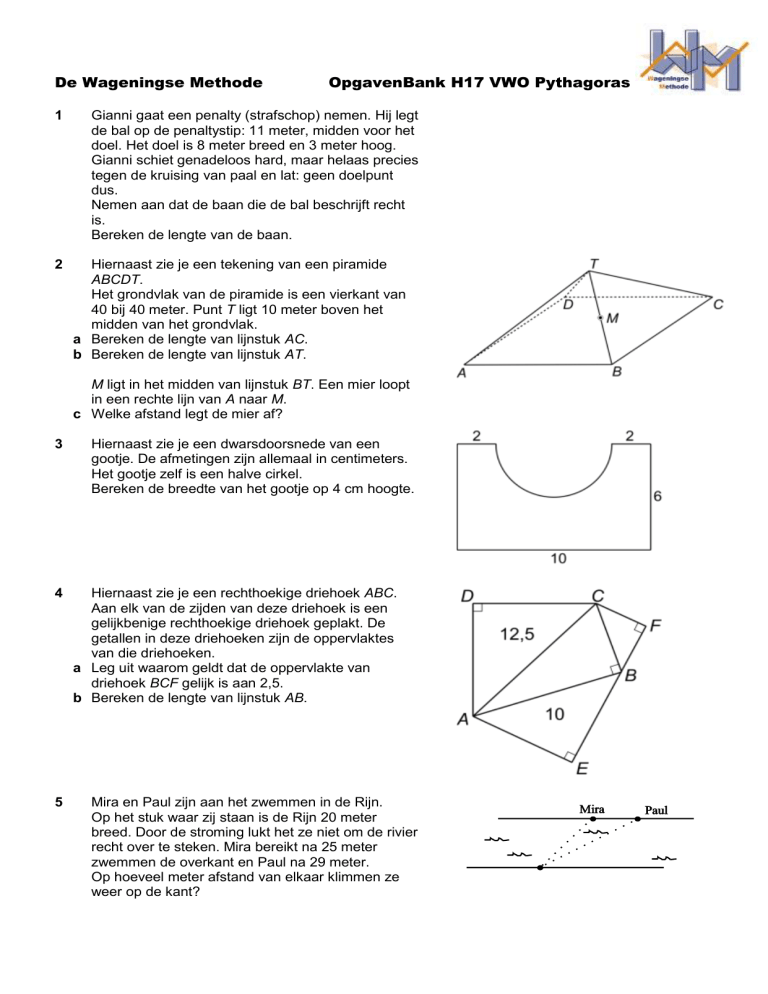
Hiernaast zie je een tekening van een piramide
ABCDT.
Het grondvlak van de piramide is een vierkant van
40 bij 40 meter. Punt T ligt 10 meter boven het
midden van het grondvlak.
a Bereken de lengte van lijnstuk AC.
b Bereken de lengte van lijnstuk AT.
M ligt in het midden van lijnstuk BT. Een mier loopt
in een rechte lijn van A naar M.
c Welke afstand legt de mier af?
3
4
5
Hiernaast zie je een dwarsdoorsnede van een
gootje. De afmetingen zijn allemaal in centimeters.
Het gootje zelf is een halve cirkel.
Bereken de breedte van het gootje op 4 cm hoogte.
Hiernaast zie je een rechthoekige driehoek ABC.
Aan elk van de zijden van deze driehoek is een
gelijkbenige rechthoekige driehoek geplakt. De
getallen in deze driehoeken zijn de oppervlaktes
van die driehoeken.
a Leg uit waarom geldt dat de oppervlakte van
driehoek BCF gelijk is aan 2,5.
b Bereken de lengte van lijnstuk AB.
Mira en Paul zijn aan het zwemmen in de Rijn.
Op het stuk waar zij staan is de Rijn 20 meter
breed. Door de stroming lukt het ze niet om de rivier
recht over te steken. Mira bereikt na 25 meter
zwemmen de overkant en Paul na 29 meter.
Op hoeveel meter afstand van elkaar klimmen ze
weer op de kant?
6
Hiernaast zie je een tekening van een
wegwerpbeker. Daarnaast zie je een
dwarsdoorsnede van deze beker. Het schuine
streepje stelt een roerstaafje voor dat precies tot
aan de rand van het bekertje komt.
a Bereken de lengte van de schuine rand van het
bekertje.
b Bereken de lengte van het roerstaafje.
7
Pim staat boven op de Euromast. Zijn oog bevindt
zich op dat moment 100 meter boven het
aardoppervlak.
Het is heel helder weer dus hij kan ontzettend ver
kijken.
Nu vraagt hij zich af op welke afstand hij de horizon
ziet. Hiernaast zie je een schematisch plaatje van
de situatie. Uiteraard kloppen de verhoudingen niet
helemaal. Neem voor de straal van de aarde 6400
km.
a Schat eens op welke afstand Pim de horizon ziet.
(Je krijgt hier geen punten voor)
b Bereken op welke afstand Pim de horizon ziet.
C
8
a
b
c
d
9
10
De hokjes in het gestippelde rooster hieronder zijn 1
bij 1. A, B, C en M zijn roosterpunten. M is het
midden van BC.
Bereken AC, AB, AM en BC. Geef exacte antwoorden, dus laat eventueel wortels in je antwoord
staan.
Wat voor speciale driehoek is driehoek ABC?
Laat zien dat hoek AMB recht is.
Bereken de oppervlakte van driehoek ABC.
De driehoek hiernaast heeft zijden van 5, 14 en 15.
a Van welke hoeken kun je zonder meer zeggen dat
ze scherp zijn? Licht je antwoord toe.
b Ga met een berekening na of de driehoek scherphoekig, stomphoekig of rechthoekig is.
M
B
A
A
B
14
15
5
C
X
Vanuit X zijn drie verbindingslijntjes naar lijn l getekend. XC staat loodrecht op l. De lengten van de
verbindinglijntjes staan in de tekening.
Bereken BC en AB.
13
20
12
l
A
B
C
11
Er worden steeds meer kunstmatige sneeuwpistes
gebruikt. Hiernaast zie je er een in de vorm van een
driezijdig prisma. De grensvlakken bestaan uit
rechthoekige driehoeken en rechthoeken. De maten
die ter zake doen zie je in de tekening.
Dolfie is ervaren en suist recht naar beneden (de
gestippelde route).
a Bereken de exacte lengte van zijn route, laat
eventueel een -teken staan.
Dolfie
20
Jaap
90
60
Jaap is beginner en gaat van rechtsboven naar
linksonder naar beneden.
b Bereken de exacte lengte van zijn route.
12
Een recht blok van 4 bij 4 bij 7 wordt doorgezaagd.
Het zaagvlak gaat door twee hoekpunten van het
blok en ook door het midden van twee ribben. Het
zaagvlak is in de tekening hiernaast gestreept.
a Wat is de vorm van het vierhoekig zaagvlak?
b Bereken de oppervlakte van het zaagvlak, doe dat
in één decimaal nauwkeurig.
13
Hiernaast is een cirkel getekend, met diameter 8.
In de cirkel is een regelmatige zeshoek getekend.
De hoekpunten van de zeshoek liggen op de cirkel.
Bereken de oppervlakte van de regelmatige zeshoek.
Tip: de zeshoek bestaat uit zes regelmatige
driehoeken.
14
ABCD is een rechthoek van 4 bij 7. Op zijde BC ligt F
zó, dat CF = 1 en op zijde AB ligt E zó, dat AE = 3.
a Bereken de exacte lengte van de zijden van
driehoek DEF.
b Ga met een berekening na of driehoek DEF
rechthoekig is.
7
D
C
1
F
4
A
3
E
B
15
Balk hiernaast is 6 bij 6 bij 5 dm.
a Bereken de lengte van de langste stok die in de balk
past (dus de lengte van AG) in cm nauwkeurig.
H
G
E
F
5
D
A
Een stok van 9 dm lengte wordt in de balk gezet.
Het ene uiteinde van de stok komt in A en het
andere ergens op ribbe CG.
b Bereken hoe hoog dat uiteinde boven het grondvlak
van de balk komt.
5
A
C
6
6
B
?
9
6
6
G
Een spin kruipt van A naar G over de zijvlakken van
de balk, langs de kortste weg.
c Bereken de lengte van die weg
Tip: doe dat via een uitslag van de balk.

A
16
Hiernaast is een skikunstbaan getekend. De maten
(in m) staan in de figuur. De achterkant staat
verticaal.
a Bereken de oppervlakte van het hellende vlak (dit is
rechthoekig).
9
12
16
Een beginneling neemt de helling van linksboven
naar rechtsonder.
b Bereken de lengte van de weg die hij aflegt in cm
nauwkeurig.
17
Een buis heeft een binnendiameter van 50 cm. Een
balk van 14 cm dik past precies in de buis.
Bereken de breedte van de balk.
14
50
?
18
Wim gaat een tent maken van 5 meter lang, 2,4
meter breed en 1,6 meter hoog. Het dak bestaat uit
twee rechthoeken. De voor- en de achterkant zijn
gelijkbenige driehoeken.
a Hoeveel m2 heeft Wim voor het dak nodig?
b En hoeveel m2 voor de voor- en achterkant samen?
Voor de tent heeft Wim (in het verlengde van de
nok) een scheerlijn gespannen. De haring waarmee
die in de grond is bevestigd, staat 1,5 meter van de
tent.
c Bereken de lengte van de scheerlijn in cm
nauwkeurig.
19
Hiernaast is de balk ABCD.EFGH getekend.
Het grondvlak van de balk is 4 bij 4 en de hoogte is
6.
M is het midden van het bovenvlak.
a Bereken de lengte van BG, AG en AM.
Schrijf het antwoord met een wortel en geef een
benadering in één decimaal.
H
G
M
E
F
X
Op ribbe AE ligt een punt X, zó, dat MX lengte 3
heeft.
b Bereken de lengte van EX.
Tip: noem EX = x.
C
D
A
20
In een rechthoekige driehoek ABC, zie hiernaast,
zijn de rechthoekszijden x – 3 en 16. De langste
zijde is 3x – 1.
Stel een vergelijking op in x en bereken daarmee
21
Hiernaast is een ruit ABCD getekend in een rooster.
In een ruit staan de diagonalen loodrecht op elkaar
en snijden elkaar precies middendoor.
a Bereken de lengte van beide diagonalen.
b Bereken de omtrek van de ruit.
c Bereken de oppervlakte van de ruit.
B
D
C
A
B
22
De hokjes in het rooster hiernaast zijn 1 bij 1. A, B,
C en D zijn roosterpunten.
a Bereken de oppervlakte van vierhoek ABCD.
b Bereken de totale omtrek van vierhoek ABCD exact
(dus met
-tekens er in).
Rond ook je totale omtrek af op 1 decimaal.
In het rooster zit ergens een roosterpunt M zodat
AM lengte 29 heeft.
c Geef een roosterpunt aan waar M kan zitten. Schrijf
er de letter M bij.
23
24
25
Hiernaast is een driehoek ABC getekend. De maten
staan er bij.
Laat met een berekening zien of driehoek ABC
rechthoekig, stomphoekig of scherphoekig is.
In de balk is een driehoek ABC getekend.
C ligt op een kwart van de zijde en B ligt in het
midden van de zijde.
a Bereken exact (dus met een
-teken) de totale
omtrek van driehoek ABC.
b Laat met een berekening zien of driehoek ABC
rechthoekig, stomphoekig of scherphoekig is.
De doosjes waarin de chocoladerepen van het
Zwitserse merk Toblerone zitten, hebben de vorm
van een driezijdig prisma.
Alle rechthoekige vlakken van dit prisma zijn 25 cm
lang en 3,9 cm breed.
De andere twee vlakken hebben de vorm van een
gelijkzijdige driehoek.
Bereken de oppervlakte van zo’n driehoek. Rond je
antwoord af op 1 cijfer achter de komma. Laat
duidelijk zien hoe je het berekend hebt.
26
In driehoek ABC is vanuit C is een hoogtelijn
getekend.
Laat met een berekening zien of ACB recht, stomp
of scherp is.
27
In een rechthoekige driehoek ABC, zijn de
rechthoekszijden x – 2 en 12.
De langste zijde is 2x – 1.
Stel een vergelijking op in x en bereken daarmee de
maten van de driehoek.
28
Een schip vaart met constante snelheid. Waar het
schip zich op de hele uren bevindt, is hiernaast
aangegeven. In R staat een radarpost.
a Bereken de snelheid van het schip in km/u. Gebruik
een wortel in je antwoord en rond af op 1 decimaal.
b Vul de tabel in (zo nodig met wortels). Je hoeft geen
berekening te geven.
Tijdstip
(uur)
Afstand
tot R (km)
1
1 31
2
3
3 32
4
c Teken zo netjes mogelijk hiernaast de bijbehorende
grafiek.
d Hoe laat is het schip het dichtst bij de radarpost?
e Bereken de kleinste afstand van het schip tot de
radarpost?
29
In een rechthoekige driehoek ABC, zijn de
rechthoekszijden x – 3 en x + 3.
De langste zijde is 30.
Stel een vergelijking op in x en bereken hoelang de
twee rechthoekszijden zijn.
30
Gegeven is een vierkant ABCD. Op de zijde AB ligt
het punt E en op het verlengde van AD (aan de kant
van D) ligt het punt F.
Er geldt DF = EB = 13 en EF = 66.
Bereken de oppervlakte van vierkant ABCD.
Tip: noem de lengte van AD x.
31
In het rooster hiernaast is elk hokje 1 bij 1.
Teken in het rooster, vanuit A, exact een lijnstuk van
lengte 40.
Teken, vanuit B, exact een lijnstuk van lengte 34.
32
•
B
A
•
In het plaatje is BC = 12, ADC = ABD = 90° en
C = 60°.
a Bereken A en BDA.
b Bereken de lengte van CD, BD, AD en AB exact.
Dus laat wortels in je antwoord staan!
D
A
33
34
B
12
C
Een luchtballon zit aan een touw van 150 meter
lengte vast. Door de wind gaat de ballon 100 meter
opzij.
a Maak een tekening van de situatie en zet de maten
bij de tekening
b Bereken hoeveel meter de ballon boven de grond
hangt.
Toon aan dat geldt dat h2 = pq.
D
a
A
h
p
b
B
q
C
35
Op de zijden van een rechthoekige driehoek zijn
gelijkbenige rechthoekige driehoeken U, V en W
getekend. De oppervlakte van V is 18 cm2, de
oppervlakte van W is 72 cm2.
Bereken de oppervlakte van U. Licht je antwoord
toe.
36
Driehoek ABC past precies in de rechthoek van 24
bij 35 cm.
a Bereken de oppervlakte van driehoek ABC.
b Bereken de lengte van de zijden van driehoek ABC
exact.
c Ga met een berekening na of driehoek ABC
rechthoekig, stomphoekig of scherphoekig is.
37
Hiernaast zie je een trapezium ABCD.
De hoeken B en C zijn recht.
Bereken AB.
38
Gerd staat 12 meter voor een boom. Gerd is 1,85
meter lang. Als Gerd naar het hoogste punt van de
boom kijkt (is de stippellijn) is die afstand 194 dm.
Bereken de hoogte van de boom. Rond je
antwoord af op hele dm.