Bewijzen met driehoeken

Bewijzen met driehoeken.
1.
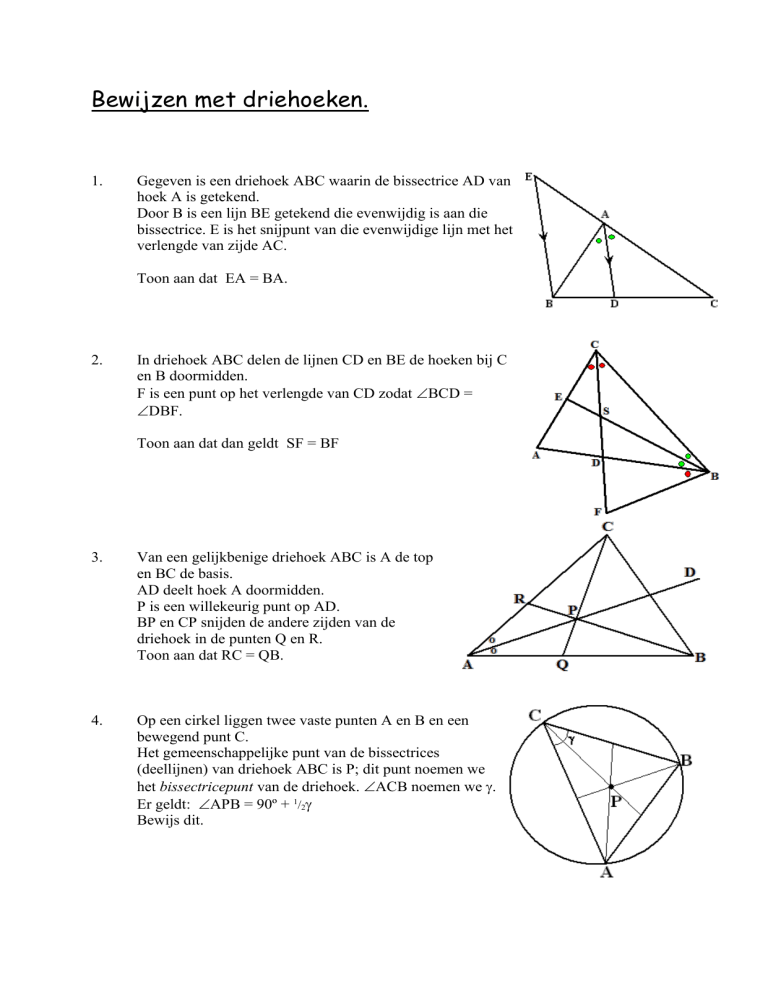
Gegeven is een driehoek ABC waarin de bissectrice AD van
hoek A is getekend.
Door B is een lijn BE getekend die evenwijdig is aan die
bissectrice. E is het snijpunt van die evenwijdige lijn met het
verlengde van zijde AC.
Toon aan dat EA = BA.
2.
In driehoek ABC delen de lijnen CD en BE de hoeken bij C
en B doormidden.
F is een punt op het verlengde van CD zodat BCD =
DBF.
Toon aan dat dan geldt SF = BF
3.
Van een gelijkbenige driehoek ABC is A de top
en BC de basis.
AD deelt hoek A doormidden.
P is een willekeurig punt op AD.
BP en CP snijden de andere zijden van de
driehoek in de punten Q en R.
Toon aan dat RC = QB.
4.
Op een cirkel liggen twee vaste punten A en B en een
bewegend punt C.
Het gemeenschappelijke punt van de bissectrices
(deellijnen) van driehoek ABC is P; dit punt noemen we
het bissectricepunt van de driehoek. ACB noemen we .
Er geldt: APB = 90º + 1/2
Bewijs dit.