Wat is druk

THEORIEVRAGEN
1) Wat is druk? Leid af voor een gas en een vloeistof. Waarom mag je spreken
over druk van een gas?
Begrip dat kracht verspreid over een oppervlak meet = DRUK
pg 
Fn
A
pin Q  lim
A0
Fn dFn

A dA
Door een systeem te beperken tot een bepaalde ruimte  druk in het systeem
Botsingen met de wand  druk op de wand
Oppervlakje binnen het systeem  botsingen hiertegen  inwendige druk
Arbeid door drukkracht van een fluïdum
Cilindervormig vat met zuiger
Botsingen van fluïdumdeeltjes op zuiger  kracht  zuiger
Fx  pA
Arbeid geleverd dr Fx bij verplaatsing van de zuiger van x naar x+dx:
W  Fxdx  pAdx  pdV
Arbeid verricht dr fluïdum bijverplaatsing van de zuiger van x 1 naar x2
V2
W1 2   pdV
V1
Arbeid is positief als V toeneemt
Arbeid verricht dr de uitwendige krachten op fluïdum is tegengesteld aan de arbeid verricht dr
het fluïdum (actie en reactie)
In grafiek: V1 < V2: Arbeid is oppervlakte onder de kromme
V1 > V2: Arbeid is tegengesteld aan oppervlakte onder de kromme
p
p
0
V1
V2
V
0
V1
V2
V
Kringproces: macroscopische begintoestand = macroscopische eindtoestand
Positief: in uurwijzerzin doorlopen
Negatief: in tegenuurwijzerzin doorlopen
Bij een gas veroorzaken de botsende gasdeeltjes de druk
1
2) Kathodestraalbuis
y
Duidelijkere tekeningen: zie cursus
x
In het elektronenkanon wordt een elektronenstraal gegenereerd. De straal wordt eerst dr een
horizontaal gericht veld afgebogen, dan dr een verticaal gericht veld.
Dan treft de straal een fluorescerend scherm waar ze een lichtpunt opwekt.
De buis is luchtledig.
In het elektronenkanon worden vrije elektronen gevormd en versneld zodat ze dezelfde snelheid
hebben.
Tussen de verticale platen: horizontaal gericht veld  horizontale kracht en horizontale
verandering van de snelheid  horizontale afbuiging.
Analoog tss de horizontale platen.
AFBUIGSYSTEMEN
y
hoek tss vg en v0 = 
vg

Fe
v0
vy
E
ev0
z

E
d
E  v0


D

Fe  e E  m a
Tussen de platen:
ay 
e
E
me
vy  aytd 
en
ed
E
mev 0
td 
d
v0
Buiten de platen:
Geen kracht meer
Snelheidsvector constant
2
Hoek afbuiging: 
tg 
~E
vy
ed

E
v0 v0²me
Hoe groter E, hoe groter de afbuiging
3) Snelheidsfilter
Elektrisch veld en magnetisch inductieveld
Totale kracht van beide velden op q:
  

F  q E v B 


Beweging van een lading, homogene velden, loodrecht op elkaar
Fe en Fm werken elkaar tegen

B 

E






 






q   
a   E v B 
m



E
Fm



B 
v
Fe

F
F  ma  a 
m




Geen versnelling (dus ongestoord door beide velden) ALS:





E   v B  B v
OF


E
E

 en B gegeven  : v0 
B


v groter  Fm > Fe  afwijking naar boven
v kleiner  Fe > Fm  afwijking naar beneden
Om deeltjes met een bepaalde snelheid te selecteren:
Deeltjes sturen door gebied waar elektrisch veld loodrecht staat op magnetisch veld en waarvan
de verhouding van de grootte van E en B gelijk is aan de gewenste snelheid.
4) Massaspectrograaf
Gebied waarin een homogeen magnetisch veld heerst

Ladingen met een bepaalde snelheid v worden loodrecht in dit veld geschoten  cirkelbaan




m a  F m  e v B

m a n  evB
an 
v²
mv²
 ma n 
 evB
r
r
mv
r
eB
3
 De straal is evenredig met de massa
 Als alle andere grootheden constant gehouden worden, kunnen ladingen met verschillende
massa’s gescheiden worden
Kernen van een element (= samenstelling verschillende isotopen, verschillende massa) dezelfde
snelheid geven door snelheidsfilter
Bundel van deeltjes door homogeen magnetisch veld sturen


v B
Deeltjes met verschillende massa ~ cirkelbaan met verschillende straal
 verschillende isotopen scheiden
q
q
q
v

: Als je niet weet, kan je door v, r en B berekenen
m rB
m
m












 B
 
 

 












B



5) Cyclotron
Geladen deeltjes versnellen met elektrische velden MAAR zeer grote velden nodig
Homogeen magnetisch veld kan de grootte vd snelheid niet veranderen: F m  v
T

B


E
B
A
Ladingen vertrekken in de bron en worden versneld door het elektrisch veld tss de 2 D’s
 ladingen beschrijven cirkelboog
r
mv
qB




m a  F m  e v B
ma n  evB
v²
mv²
 ma n 
 evB
r
r
mv
r
eB
an 
4
Ladingen keren terug nr het gebied tss de 2 D’s
Alternator heeft het elektrisch veld van richting veranderd
 ladingen worden versneld en beschrijven een cirkelboog met grotere straal in de 2 de D
enz.
Bij het verlaten van het cyclotron worden de deeltjes naar een doelwit T gericht
6) Bespreek de mechanische resonantie van de gedempte trilling adhv de veer en
adhv de fasorvoorstelling
Systeem ondervindt naast terugroepende kracht en dempingskracht ook sinusoïdaal variërende
kracht.
Systeem kan reageren met een amplitude die veel groter is dan de amplitude van de aandrijving:
RESONANTIE.
Model: bolletje aan verticaal opgestelde veer
Bolletje beweegt in vloeistof en ondervindt harmonisch variërende kracht
k en m: cte
Grootte van de demping en frequentie van de aandrijving kunnen variëren.
DIFFERENTIAALVERGELIJKING (2DE WET VAN NEWTON)
d²x
dx
m

 kx  Ad sin t
dt²
dt
d²x  dx k
k

k

 x  Xd sin t

en  0²
dt² m dt m
m
2m
m
d²x
dx
 2
 0²x  0²Xd sin t
dt²
dt
 Systeem gaat trillen met de frequentie van de aandrijving
xs  X sint   : stationair e oplossing
d²x s
dxs
 2
 0²xs  0²Xd sint 
dt²
dt
0²xs  0²X sint  
2
dxs
 2X cos t  
dt
I
II

 2X sin( t    )
2
d²x s
 X²sint  
dt²
III
Som moet de projectie van de vector zijn die de trilling 0²Xdsint   voorstelt
5
FASORVOORSTELLING
III
II
Som
I
Hoek tussen x-as en som: t
Hoek tussen x-as en I: t + 
y
x
STELLING VAN PYTHAGORAS
Amplitude van de som = amplitude van II + (amplitude van I – amplitude van III)
0 4 Xd²  2X²  0²X  ²X²
 X²2²  0²  ²²
X² 
0 4 Xd²
Xd

2²  0²  ²²  2  ² 
²

²   1 
 0²   0²
Uit figuur:
tg 
 2
0²  ²
0 <  <-  uitwijking volgt op de aandrijving
X
 = 0  geen demping
Xd
0²
1
²
 heel klein : X  Xd
  0 : x  Xd
  0 : Xd  
  0 :   
X0
  0: Max X? Amplitude systeem (X) kan groter zijn dan amplitude aandrijving (X d)

1
X

 frequentie interval waarvoor
1
0
Xd
2
 Versterkin g van het inputsigna al (kan zeer groot zijn voor een zeer kleine demping)
6
Amplitudekarakteristiek maximaal:

  0 1 - 2 ²
 0 
Maximum naar links en maximale waarde daalt als demping stijgt
Demping te groot :

1

 X  Xd
0
2
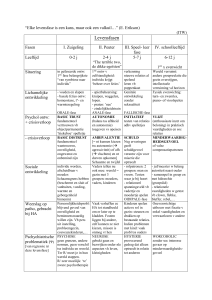
7) Bespreek de wetten van Ohm
Stroom van positieve ladingen in tijdsinterval t stromen in het volume van de cilinder tussen de
vlakken a en b en door de doorsnede A.
N: aantal ladingen per volume
q: lading van een deeltje
b
a
x=vdt
Q  nqAx   nqAvdt 
I
Q
 nqAvd
t
MICROSCOPISCHE VORM


Driftsnelheid : vd   E d
I
Stroomdich theid : J 
A
dI
J
 nqv d
dA


J  nq v d

en



v d   E d

 J  nq E  n q  E
Conductivi teit :   n q 


J  E
Re sistivitei t :  
1
1

 n q



E
J
of E   J


MACROSCOPISCHE VORM
I  nqvdA  n q AE


v d   E d
7
Spanning over een geleider : U  El  E 
n q a
U
l
l
R
n q A
U
l
I
I
U
R
1
(conductan tie)
R
I  G U - Ud 
G
8)Bespreek de elektrische weerstand. Is I altijd evenredig met U?
R
U
: Wet van Ohm
I
Weerstand van een geleider is afhankelijk van zijn afmetingen
l
A
 is temperatuu rsafhankel ijk
R
 metalen geleider : elektronen wordne versneld dr elektrisch veld
elektronen worden afgeremd dr botsingen met ionen
Temperatuu r stijgt  ionen trillen heviger om evenwichts positie
 kans op botsing tss elektronen en ionen is groter
 grotere weerstand bij hogere temperatuu r
(niet vr alle geleiders)
R - R0  R0T - T0 
  0 : PTC : grotere weerstand bij hogere temperatuu r
α  0 : NTC : kleinereweerstand bij hogere temperatuu r
Energieomzetting in weerstand  warmteontwikkeling
Elektronen botsen tegen ionen en geven een deel van hun E k aan de ionen
De gemiddelde kinetische energie van de ionen neemt toe
Temperatuur stijgt
8
WEERSTANDEN IN SERIE
I: cte
2
I
R1
R
1
U
U


3
R2
R3
2de wet van Kirchoff
U-R1I-R2I-R3I=0
 R=R1+R2+R3
U-RI=0
n
R   Ri
i1
WEERSTANDEN IN PARALLEL
3
2
1
R1
R2
R3
4
5
8
U


R
U
I
7
U  V61  I3R3
I1
I
6
1=2=3
I3
U  V52  I2R2
U  V43  I1R1
U
R1
R2
R3
I
4=5=6
Eerste wet van Kirchoff
I-I1-I2-I3=0
I1 
U
R1
I2 
U
R2
I3 
U
R3
I 1
1
1
 

U R1 R 2 R 3
1
1
1
1
 

R R1 R 2 R 3
Is I altijd evenredig met U???????
9
9) Bespreek het verband tussen U en I bij RC op gelijkstroom
RC-schakeling: weerstand en condensator in serie geschakeld
R
C
I
s
Opladen door kring te sluiten
q
C
V1  V 2  U
Uc 
R
V1
C+
+
+
-
V2
Spanning over C stijgt
Op linkerplaat steeds hogere potentiaal: 0  V1
 V tussen positieve pool van de bron en linkerplaat wordt steeds kleiner
Ladingen ondervinden een kleinere kracht
 Snelheid en stroom nemen af
2de wet van Kirchoff
Vbron  VR  VC  0
U - iR -
q
0
C
i : kleine letter : tijdsafhan kelijk
dq
positieve stroom ~ stijgende q
dt
dq q
U-R
  0 Differenti aalvgl eerste orde
dt C
dq q
UC


dt RC RC
t


q  UC 1  e RC 
  RC
Qmax  UC


U t
I  e RC
R
dq
In stationair regime :
0
dt
Eindlading : q  UC
i
t


q
 U 1  e RC 
c


  RC
Uc 
10
Uc
U
RC
2RC 3RC
Voor stroom: uitdrukking vr q afleiden:
it  
t
U RC
e
R
UR  iR
i
UR
R
Stroom neemt exponentieel af
C : systeem bereikt sneller stationair regime
Ontladen: U daalt exponentieel
C+
-
R
I
schakelaar toe: positieve en negatieve plaat met elkaar verbonden
 stroom van positieve nr negatieve plaat
s
2de wet van Kirchoff
q
 IR  0
C
q dq

R0
C dt
q dq

RC dt
t
q  Q 0e RC
it  
q  i 
- dq
dt
Q0 : beginlading  UC
na opladen met zelfde weerstand
t
Q RC
e
RC
11
10) Wat is diffusiespanning? Wat zijn de voorwaarden voor dit verschijnsel? Hoe
kom je aan de formule
H 2O
Na+ClNa+Cl-
diffusiekracht
V 2  V1 
 kT c2
ln
Q
c1 ?
Na+Cl- + +
Na+Cl- Na+ClNa+Cl- + +
Na+Cl+ +
c1
>>
c2
+
wand: semi-permeabel vr Na+
dr concentratieverschil: diffusie
° potentiaalverschil  spanning
Voorwaarden: concentratieverschil, semipermeabele wand die 1 soort ionen doorlaat

E
elektrische kracht
Diffusiekracht wordt tegengewerkt door elektrische kracht
Hoe meer ionen er verplaatst worden, hoe groter het veld wordt
Na zeker tijd zijn de 2 krachten even sterk geworden: DYNAMISCH EVENWICHT
Model: enkel Na+ ~ ideaal gas dr H2O tss Na moleculen
Na+
p(x)
p(x+x)
Na+
x
x
x+x
px  x   px  dp

(definitie afgeleide)
x
dx
dp
px  x   px  
x
dx
n
c
pV  nRT
V
n
p  RT  cRT
V
x  component vd diffusiekr acht :
Fdx  px A  px  x A
 px   px  x A  

 dc
RTxA
dx
dp
xA
dx
x - component vd elektrisch e krac ht :
Fex  Exq
q  NAnq
en
n  cV
 NAcVq  NAcxAq
Ex 
- dV
(potentiaa l! )
dx
12
Resultante vd krachten is nul
Fdx  Fex  0
Fdx  -Fex
dc
dV
RTxA 
NAcqxA
dx
dx
 RT dc
dV 
NA q c
-
2
1 dV 
 RT dc
RT
 V2  V1  
(ln c2  ln c1)

NA q c
N Aq
-
V2  V1  
RT c2
ln
NAq c1
RT c2
ln : Nernstpote ntiaal
NAq c1
11) Geef de formule vr de stroom I in een RLC-kring met wisselspanning
RLC-kring: bron, weerstand, condensator en inductiespoel in serie
u~
C
R
Harmonische spanning:
ut   U sint 
it   I sint  
L
Fasorvoorstelling vr U & I
UL
U
I
UR
UC
Hoek met UR: t+
Hoek met U:t
1
I
C
UL  XLI  LI
UC  XCI 
UR  RI
2de Wet van Kirchoff
u=uC+uL+uR
13
  2f
Stelling van Pythagoras
U²  UR²  Ul  UC ²
1 

U²  R²I²   L 
²I²
C 

U
I
1 

R²   L 
²
C 

1 

 L 

C 

tg  
R
Amplitude hangt af van de frequentie
Stroom is maximaal als  
1
LC
Dan is de kring in RESONANTIE
12) Bespreek Ep en krachtwerking van een systeem van twee moleculen. Gebruik
redenering olv het concept energie. Leg uit wat bindingsenergie is.


Ep,2 Fi  Ep,1 Fi  W1 2
 
 
1  dim ensionaal :

dEp Fi  dW
 
dEpFi, x   Fi, xdx (def. Arbeid)
dEpFi, x 
dx
Deeltje streeft nr min vr Ep
Fi, x  -
Ep max  labiel evenwicht
Ep min  stabiel evenwicht
3 - dimensiona al :

dEp Fi  Fi, xdx  Fi, ydy  Fi, zdz 
 
y en z constant
dEpy, z  Fi, xdx
dEpy, z  partiële afgeleide van Ep naar x : Ep
Fi, x  
dx
Ep
Fi, x  
x
Ep
Fi, y  
y
Fi, z  
x
 Componenten van de krachtvector
Ep
x
14
Vector: 1ste component: partiële afgeleide nr x
2de component: partiële afgeleide nr y
3de component: partiële afgeleide nr x
 Gradiënt vd functie


F    Ep
Ep vd wisselwerking tss 2 moleculen
Ep
r
Ep   afgeleide positief
F21
2
F12
Fr  
1
Ep   afgeleide negatief
Kracht: aantrekkend als r>rmin
Fr negatief: kracht op ene deeltje tegengesteld aan plaatsvector van dit deeltje
t.o.v. het andere
Afstotend als r<rmin
Ep
rmin
0
r
Ep min
Fr
0
r
15
13) Wat is het verschil tss warmte en temperatuur? Leid de formule af V1p1=V2p2
voor een adiabatisch proces.
2 systemen in thermisch contact als er energie uitwisseling mogelijk is zonder dat er
mechanische arbeid geleverd wordt. De uitgewisselde energie is WARMTE.
Als de energie uitwisseling stopt  thermisch evenwicht, de 2 systemen hebben dezelfde
temperatuur
 Enkel warmteoverdracht tss systemen met verschillende temperatuur.
TEMPERATUUR is een maat vr de Ek, inw per deeltje van een systeem.
3
pV pV  NkT
2
3
U  NkT
2
U
Adiabatisch proces: systeem thermisch geïsoleerd vd omgeving, kan met de omgeving enkel
mechanische energie uitwisselen
Q  0
1ste wet van de thermodynamica
dU  W
W1 2  U1  U2 
Systeem kan enkel arbeid verrichten dr verandering van inwendige energie
Uitzetting: W positief, U 
Ideale gaswet: pV= nRT
Geïsoleerd 
dU  ncvdTdU  W  dU  pdV  0
pdV
cv
dpV   nRdT
ndT  
(ideale gaswet)
Vdp  pdV  nRdT
R
pdV
cv
cvVdp  cvpdV  RpdV
Vdp  pdV  
cvVdp  cv  R pdV
cvVdp  cp pdV
dp
cp dV

p
cv V

cp
cv
 p1 
 V2 
ln     ln 
p
2
 V1 
 
V1  p1  V 2  p2
16
14) Geef de microscopische beschrijving van een ideaal gas
Ideaal gas: model vr verdund gas
N identieke puntmassa’s, onderlinge interactie wordt verwaarloosd
Enkel elastische botsingen met wanden van het vat
Geen kinetische energie uitgewisseld met wand
Onderling ook geen kinetische energie uitgewisseld  kinetische energie: constante
vgxt
c
z
n
m0vi² m0 n
U

vi²
d
2 i 1
i 1 2
vg
b
y
n
1
a
vg² 
vi²



N i 1
U
m0 n
m0vg²
vi²  N

2 i 1
2
Druk op wand abcd?
 x-component vd gemiddelde kracht van de deeltjes op de wand
Elastische botsingen met de wand  verandering van hoeveelheid beweging
p  m0 vgx  m0 vgx  2m0 vgx
Fx  
p 2m0 vgx

t
t
Aantal deeltjes tegen de wand in tijdsinterval t?
N
V
 helft in volume met basis abcd (oppervlakte A) en hoogte vgxt botsen
- deeltjes per volume :
andere helft gaat verkeerde kant uit
 Aantal deeltjes in dit volume :  vgx t A
N
V
1
 vgx t A N 2m0 vgx
2
V
t
N
 A m0vgx²  druk  delen door A
V
N
p  m0vgx²
V
1
vgx²  vgy²  vgz²  vg²  vgx²  vg²
3
1N
p
m0vg²
3V
2 m0vg² 2
2
pV  N
 U  Nu met u  inwendige energie per deeltje
3
2
3
3
Rx 
17
x
15-16)Bespreek de wet van arbeid en mechanische energie (uitgaande van arbeid
en kinetische energie)
Wet van arbeid en mechanische energie: verandering van energie van een puntmassa=arbeid van
de niet conservatieve krachten (afhankelijk van de gevolgde weg)
1 kracht
zw
zw
W1 2  - E p,2- E p,1 


E k , 2  E k ,1  W 1 2
zw
zw
Ek,2  Ek,1  - E p,2- E p,1 


zw
zw
Ek,2  E p,2  Ek,1  E p,1

Als deeltje 1 conservatieve kracht F i ondervindt




Ek,2  Ek,1  W1 2   Ep,2 Fi  Ep,1 F i 












Ek,2  Ep,2 Fi  Ek,1  Ep,1 F i
 
 
(Wet van behoud van energie)
Meerdere krachten : conservati eve en niet conservati eve
n 
k 
F  F

i1
i1
i
m 
i, c
  F i, nc
i1

k r2
W1 2  
F
i1 

k r2
r
m

i, c
dr  

r1 

i1 
r
1

F i, ncd r
2
k


 
  
F
i,
c
d
r


 Ep,2 Fi, c   Ep,1 F i, c  



 


i1 
i1 
r1
m

r1 


i1 
r
nc

F i, ncd r  W 1 2
2
Ek,2  Ek,1  W1 2
(Wat arbeid en kinetische energie)
k


nc


 Ek,2  Ek,1    Ep,2 Fi, c   Ep,1 F i, c    W 1 2
 

 
i1 
k
k


nc


Ek,2   Ep,2 Fi, c    Ek,1   Ep,1 F i, c    W 1 2




  


i1
i1
Mechanische energie van een systeem is de kinetische energie + alle vormen van potentiële
energie
k

E  Ek,2   Ep,2Fi, c
 
i1
Bondige vorm wet van arbeid en mechanische energie:
nc
E2  E1  W 12
18
Als de niet conservatieve krachten geen arbeid leveren:
E2=E1  Wet van behoud van mechanische energie
17)Leid de uitdrukking af voor entropieveranderingen bij een isotherm proces
Geïsoleerd systeem
  
 V0/2
  
  

V0/2












Gas levert geen arbeid: drukkracht staat loodrecht op de verplaatsing
Geen warmte uitwisseling met de omgeving
W  0
Q  0
Inwendige energie verandert niet, ISOTHERM proces
Waarom vult gas heel de ruimte?
- Aantal mogelijkheden om 1 deeltje in V0 te plaatsen is evenredig met V0
- Als verschillende deeltjes op dezelfde plaats kunnen zitten:
* Aantal mogelijkheden om N deeltjes in V0 te plaatsen is evenredig met V0N
* Aantal mogelijkheden bij V0/2 is evenredig met (V0/2)N
Evenredigheidsfactor wordt bepaald dr aantal mogelijkheden vr de snelheid
 Aantal is gelijk omdat inwendige energie gelijk is
Snelheidswaarden moeten voldoen aan:
N
U
i1
m0vi²
2
N
 V0 
 
Waarschijn lijkheid deeltjes links
2
  N  2 N
Waarschijn lijkheid deeltjes overal
Vo
voor N  10 23  0
Quasistatische overgang: transformatie van een toestand naar een andere via
evenwichtstoestanden
  
 V 
  



V+V





V0
2
Eindvolume : V 0
Beginvolume :
19

T verandert niet  inwendige energie verandert niet
Q1 2  W1 2
V klein genoeg  W  pV
 Q12  pV  NkT
V
V
Aantal microtoest anden V  V V  V 
V 
Q1 2 



 1 
  1 

N
Aantal microtoest anden V
V
V 

 NkT 
Q1 2 
Q1 2
 Aantal microtoest anden V  V 

ln
klein
  N ln 1 
 grote N 
Aantal
microtoest
anden
V
NkT
NkT




Q1 2 Q1 2
N

NkT kT
Q1 2
k lnaantal microtoest andenV  ΔV   k lnaantal microtoest anden V  
T
Entropie : S  S0  k lnaantal microtoest anden bij thermodyna mische toestand 
N
N
J 
 K 
SV  V   SV  
Q12
T
N
niet afhankelij k van de gevolgde weg
Geïsoleerd systeem evolueert zo dat de entropie toeneemt
Evenwichtstoestand van een systeem = toestand van maximale entropie
Systeem evolueert zo dat de entropie van het systeem en de omgeving toenemen
Evenwichtstoestand = toestand van maximale entropie van systeem en omgeving
20
18) Leid de formule af voor eendimensionale volkomen elastische botsingen en
bespreek.
Elastische botsing: hoeveelheid beweging en kinetische energie behouden.
Behoud hoeveelhei d beweging
m1v1 , x  m2v2, x  m1v'1 , x  m2v'2, x
m1 v1 , x - v'1 , x   m2 v'2, x  v2, x 
Behoud hoeveelhei d kinetische energie
m1v²1 , x m2v²2, x m1v'²1 , x m2v'²2, x



2
2
2
2
m1v²1 , x  m2v²2, x  m1v'²1 , x  m2v'²2, x
m1 v²1 , x  v'²1 , x   m2v'²2, x  v²2, x 
m1 v1 , x  v'1 , x  v1 , x  v'1 , x   m2v'2, x  v2, x v'2, x  v2, x 
samen met behoud van hoeveelhei d beweging
  v1 , x  v'1 , x   v'2, x  v2, x 
Als v'1 , x  v1 , x en v'2, x  v2, x : BOTSING
v'1 , x - v'2, x  - v1 , x  v2, x
m1v'1 , x  m2v'2, x  m1v1 , x  m2v2, x
Deze twee bij elkaar optellen
Om v'1 , x te bekomen de eerste vgl vermenigvu ldigen met m2
Om v'2, x te bekomen de eerste vgl vermenigvu ldigen met - m1
m1  m2 v'1 , x  m1 - m2 v1 , x  2m2v2, x
m1 - m2 v1 , x  2m2v2, x
v'1 , x 
m 1  m2
m1  m2 v'2, x  2m1v1 , x  m2 - m1 v2, x
2m1v1 , x  m2 - m1 v2, x
v'2, x 
m1  m2
21
19)Hoe komen we aan de formule vr relativistische energie?
Relativiteitstheorie:
Massa afhankelijk van de snelheid: sneller  ‘zwaarder’

m v  
 
m0
 m 
d
v 



F
dt

r 1
m0 : rustmassa; c : lichtsnelh eid
v²
1
c²

W1 2   F d r

r2

r1



r2
r2
r1

 dv²

d r r 1 
 W1 2  d m v 
  v  md v  vdm     m
 v²dm 

 dt  

  2


r2
m0   mv  1 
v²
c²

v²
m0 ²  mv ² 1  
 c²

v²
v²
0  2mv dmv  1    mv²d
c²
 c²
v²
v²
mv d  c²  v²dmv  of mv d  v²dmv   c²dmv 
c²
2

r1
W1 2   c²dm  c²mv2   mv1 

r2
Massa oorspronke lijk in rust wordt tot snelheid v gebrahct
Arbeid verhoogt relativistische energie van m0 c² tot mv c²
m0 c² : rustenergi e
E  E0  mv c²  m0 c²  mc²
Equivalentie van massa en energie
Arbeid leidt tot veranderin g van massa
als de massa verkleint, komt er energie vrij
20)Verklaar dipool en ECG
Dipool: systeem waarin positieve en negatieve ladingen verschoven zijn tegenover elkaar zodat
gelijke positieve en negatieve ladingen op afstand l van elkaar zijn
y
Vector van negatieve nr positieve lading:
P


Dipoolmome nt : p  Ql e
r1
Potentiaal van een dipool :
kQ kQ
 1 1
V  r   V-Q  r   VQ  r   

 kQ   
 
 
 
r1
r2
 r1 r2 


r
r2

-Q p 0
+Q
l
22
x
1
l

 y²   x  
2

2
l

r2  y²   x  
2

Cartesisch e coördinate n
P
r1
2
r2




1
1
V  r   kQ

2
2
 

l
l


y
²

x

y
²

x






2
2










-Q
r

1
p
2
+Q
l
Poolcoördi naten :
r  l
l
cos 
2
l
r2  r  cos 
2
OF
r1  r 
l


r1  r 1  cos  
 2r

l


r2  r 1  cos  
 2r

1 1
l

  1  cos  
r1 r  2r

1 1
l

  1  cos  
r2 r  2r


p cos 

kQl cos 
V r  

 
r²
40r²
ECG: zenuwprikkeling voor het hart  in het hart elektrische stroom in bepaalde richting
(100A)
Elektrisch effect van het hart ~ dipoolvector
 Dipoolmoment verandert periodisch
Periode = periode waarmee het hart het bloed voortstuwt
Richting vd dipool: hartvector
Elektrische potentiaal afhankelijk vd afstand en de richting ()
Driehoek van Einthoven
Potentiaal rechterarm (RA), linkerarm (LA) en linkervoet(LV) meten. LV is nulniveau.
U1,U2 en U3 zijn de componenten vd hartvector volgens de verbindingslijnen tss beide armen, RALV en LA-LV
Grootte hartvector kan hieruit berekend worden
Tekening zie cursus (sorry schatje, geen zin meer)
23
21)Bespreek alle mogelijkheden van elastische botsingen
1-dimensionaal zie vraag 18
2-en 3- dimensionaal




m1 v 1  m2 v 2  m1 v 1'm2 v 2'
Behoud hoeveelhei d beweging
m1v1² m2m2² m1v1'² m2v2'²



Behoud kinetische energie
2
2
2
2
2 projecties v1 , x; v1 , y  v2, x; v2, y 
Te zoeken : v1 , x'; v1 , y' v2, x'; v2, y' 4 onbekenden
Extra gegeven of parameter nodig
24