symbolen met eenheden

Permanente kennis 3de trimester 4de jaar
Grootheden en eenheden
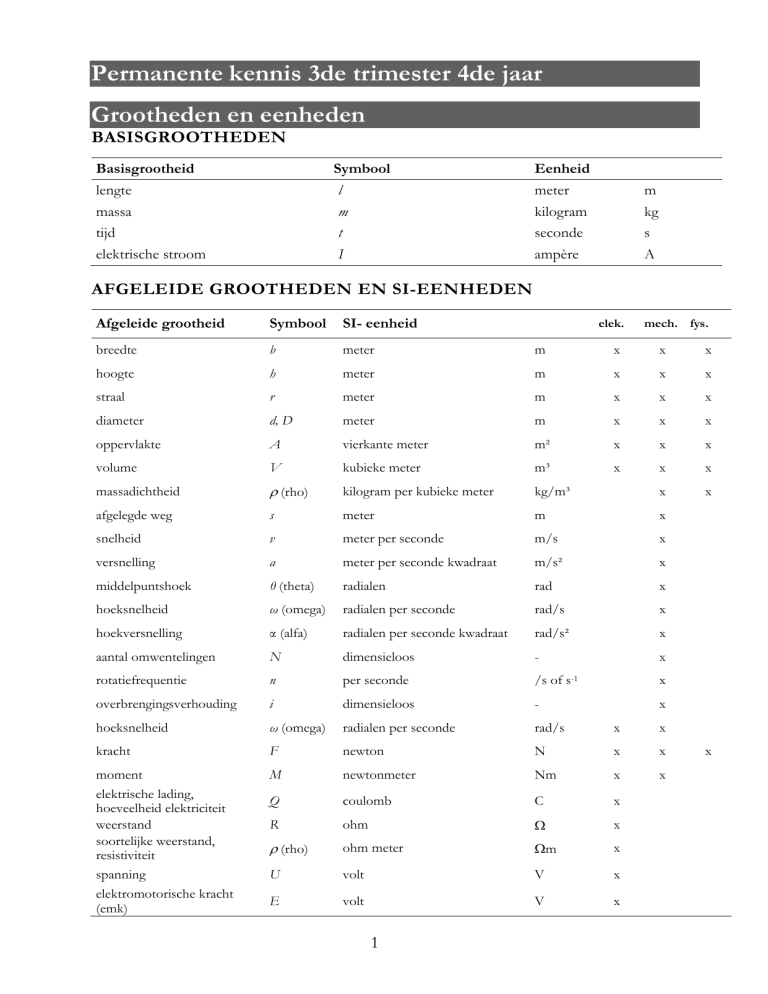
BASISGROOTHEDEN
Basisgrootheid
Symbool
lengte
massa
tijd
elektrische stroom
l
m
t
I
Eenheid
meter
kilogram
seconde
ampère
m
kg
s
A
AFGELEIDE GROOTHEDEN EN SI-EENHEDEN
Afgeleide grootheid
Symbool
SI- eenheid
breedte
b
meter
m
x
x
x
hoogte
h
meter
m
x
x
x
straal
r
meter
m
x
x
x
diameter
d, D
meter
m
x
x
x
oppervlakte
A
vierkante meter
m²
x
x
x
volume
V
kubieke meter
m³
x
x
x
massadichtheid
 (rho)
kilogram per kubieke meter
kg/m³
x
x
afgelegde weg
s
meter
m
x
snelheid
v
meter per seconde
m/s
x
versnelling
a
meter per seconde kwadraat
m/s²
x
middelpuntshoek
θ (theta)
radialen
rad
x
hoeksnelheid
ω (omega)
radialen per seconde
rad/s
x
hoekversnelling
α (alfa)
radialen per seconde kwadraat
rad/s²
x
aantal omwentelingen
N
dimensieloos
-
x
rotatiefrequentie
n
per seconde
/s of s-1
x
overbrengingsverhouding
i
dimensieloos
-
x
hoeksnelheid
ω (omega)
radialen per seconde
rad/s
x
x
kracht
F
newton
N
x
x
moment
elektrische lading,
hoeveelheid elektriciteit
weerstand
soortelijke weerstand,
resistiviteit
spanning
elektromotorische kracht
(emk)
M
newtonmeter
Nm
x
x
Q
coulomb
C
x
R
ohm

x
 (rho)
ohm meter
m
x
U
volt
V
x
E
volt
V
x
1
elek.
mech. fys.
x
DECIMALE VOORVOEGSELS
Naam
Symbool
Waarde
mega
M
106
kilo
k
103
hecto
h
102
deca
da
101
deci
d
10-1
centi
c
10-2
milli
m
10-3
micro

10-6
Je moet grootheden correct kunnen omzetten naar de gevraagde eenheid.
WISKUNDE
REKENVAARDIGHEDEN
Onderstaande rekenregels moet je kennen en kunnen toepassen.
Rekenen met breuken
a c ad  bc
 
b d
bd
Tekenregel
a c ac
 
b d bd
  a    a
   a   a
  a   a
  a   a
Distributiviteit
a  b  c   ab  ac
a c a d ad
:   
b d b c bc
 a  b  c  d   ac  ad  bc  bd
Merkwaardige producten
 a  b   a2  2ab  b2
2
 a  b   a2  2ab  b2
 a  b  a  b   a 2  b2
2
VERGELIJKINGEN – FORMULES OMVORMEN
Bij een gelijkheid mag je links en rechts dezelfde bewerking toepassen.
 Om een term uit een lid weg te werken vermeerder je beide leden met het tegengestelde van
die term.
 Om een factor uit een lid weg te werken vermenigvuldig je beide leden met het omgekeerde
van die factor.
2
MACHTEN
a m  a n  a m n
am
 a mn
n
a
a 
m n
 a  b
 a mn
n
 a n  bn
n
an
a
   n
b
b
1
an  n
a
RECHTHOEKIGE DRIEHOEKEN
Stelling van Pythagoras

c
a
c 2  a 2  b2

b
Hoeken
Sinus van een scherpe hoek in een rechthoekige driehoek
overstaande rechthoekzijde
sin Hˆ 
schuine zijde
sin  
a
c
cos  
b
c
tan  
a
b
Cosinus van een scherpe hoek in een rechthoekige driehoek
aanliggende rechthoekzijde
cos Hˆ 
schuine zijde
Tangens van een scherpe hoek in een rechthoekige driehoek
overstaande rechthoekzijde
tan Hˆ 
aanliggende rechthoekzijde
GONIOMETRIE
 360° ̂ 2 rad
 goniometrische cirkel: C(O,1): cirkel met middelpunt de oorsprong O en met straal 1
 beeldpunt of voorstelling: het snijpunt van het eindbeen van de georiënteerde hoek met de
goniometrische cirkel: coP   cos  , sin  
 grondformule van de goniometrie: cos2 + sin2 = 1

tan  
sin 
cos 
3

   tan   
 1  cos   1
 1  sin   1
 teken van de goniometrische getallen
teken van
I
II
III
IV
sin
+
+
-
-
cos
+
-
-
+
tan
+
-
+
-
 goniometrische getallen van enkele bijzondere hoeken

0°
30°
45°
60°
90°
180°
270°
360°
sin
0
1
2
2
2
3
2
1
0
1
0
cos
1
3
2
2
2
1
2
0
1
0
1
tan
0
3
3
1

0

0
3
MIDDELEVENREDIGEN IN EEN RECHTHOEKIGE DRIEHOEK

In een rechthoekige driehoek is de hoogte op de schuine zijde middelevenredig tussen de 2
stukken, afgesneden op de schuine zijde.
a'
a
c
h2  a ' b '
h
b'
b

In een rechthoekige driehoek is elke rechthoekszijde middelevenredig tussen zijn
loodrechte projectie en de schuine zijde.
a'
a'
a
c
h
a
b'
c
h
b'
b
b
a 2  a ' c
b2  b ' c
4
LENGTE VAN EEN LIJNSTUK
 AB   xB  xA 2   yB  yA 2
OPPERVLAKTE EN OMTREK VAN ENKELE FIGUREN
Rechthoek
Vierkant
h
z
z
b
A  bh
p  2b  2h
A  z2
p  4 z
Parallellogram
h
h
Driehoek
b
bh
2
A
b
A  bh
Trapezium
Cirkel
b
h
d
a
ab
A
h
2
A
 d2
4
   r2
5
p   d
 2   r
MEETKUNDIGE FIGUREN
Cirkel
koorde
straal
middellijn
diameter
Driehoek
hoogtelijnen
zwaartelijnen
EERSTEGRAADSFUNCTIES
Betekenis van a en b in f ( x)  ax  b

b bepaalt het snijpunt van de rechte met de y-as:  0, b 

a is de richtingscoëfficiënt van de rechte (rico)
a>0
a<0
a=0
stijgende functie
dalende functie
constante functie (horizontale rechte)
rico  a 
y (verplaatsing volgens y-as)
x (verplaatsing volgens x-as)

Eerstegraadsfuncties tekenen

Eerstegraadsfuncties met dezelfde rico's bepalen evenwijdige rechten!

De nulwaarde van een functie is het origineel waarvan de functiewaarde '0' is.

De nulwaarde is het snijpunt van de grafiek met de x-as.

Tekenonderzoek en tekentabel maken
6
VERGELIJKINGEN VAN RECHTEN
Cartesiaanse vergelijking van:
o een schuine rechte:
s  y  ax  b
(snijdt de x-as én de y-as)
o een horizontale rechte:
h y b
(snijdt enkel de y-as)
o een verticale rechte:
o de x-as:
vxr
y0
(snijdt enkel de x-as)
(snijdt de y-as in ‘0’)
o de y-as:
x0
(snijdt de x-as in ‘0’)
Rico van een rechte door 2 punten

a  rico 
y y2  y1 y1  y2
met  x1 , y1  en  x2 , y2  coördinaten van 2 gegeven


x x2  x1 x1  x2
punten.
Vergelijking van een rechte als een punt en de richting gegeven is

y  ax  b
met
a : rico (gegeven)
Vergelijking van een rechte door 2 gegeven punten

y  ax  b
met
a : rico zoeken met formule
Midden van een lijnstuk

M is het midden van  AB  met A  x1 , y1  , B  x2 , y2  dan
x x y y 
co  M    1 2 , 1 2 
2 
 2
Algemene vergelijking van een rechte

a' x b' y  c'
a ' , b ' en c ' 
STELSELS VAN VERGELIJKINGEN
Combinatiemethode
Substitutiemethode
PARABOOL
f ( x)  a  x 2  b  x  c

Vorm
a>0
a<0

Symmetrieas
SA  x  

Top
 b
 b 
T   , f   
 2a  2a  

Nulwaarden
x1,2 
dalparabool
bergparabool
b
2a
b  b 2  4ac
2a
7
CIRKEL
C  M , r    x  xM    y  yM   r 2
(middelpuntsvergelijking)
x2  y 2  a  x  b  y  c  0
(algemene vergelijking)
2
2
Fysica
M ASSADICHTHEID

m
V
Mechanica
B EGRIPPEN
Positie van een punt in een vlak
Middelpuntshoek
s

r
2 rad
8
360°
K INEMATICA EN DYNAMICA
rechtlijnig
Eenparige beweging
s  s0  v  t
cirkelvormig
  0    t
Eenparig veranderlijke
beweging
v  v0  a  t
  0    t
s  s0  v0  t 
Wet van Newton
a  t2
2
  0  0  t 
 t2
2
F  ma
Verband tussen de grootheden en eenheden van een rechtlijnige beweging en een cirkelvormige
beweging.
naam
rechtlijnig
grootheden
cirkelvormig
afstand
 doorlopen hoek
s
m

rad
snelheid
 hoeksnelheid
v
m/s

rad/s
versnelling
 hoekversnelling
a
m/s²
α
rad/s²
DE CIRKELVORMIGE BEWEGING
Basisformules
s  r
v r
v  d n
  2   n
Overbrenging van cirkelvormige bewegingen
i
ndrijver
nvolger

Dvolger
Ddrijver
i
n1 D2 z2


n2 D1 z1
MOMENT VAN KRACHT T.O.V. EEN PUNT

r
’
M  lF
M  r  F  sin 
F
l

De richting en zin van de momentvector worden bepaald met de rechterhandregel.
9
O
DE STELLING VAN VARIGNON (MOMENTENSTELLING)
Het moment van een stelsel van krachten ten opzichte van een punt is gelijk aan het moment van de
resultante van dit stelsel ten opzichte van hetzelfde punt.
M O FR   M O Fi
(deze stelling kunnen toepassen)
Elektriciteit
E LEKTRICITEIT - A LGEMEEN
SAMENSTELLING VAN DE STROOMKETEN




de spanningbron
de geleiders
de schakelaar
de verbruiker (het elektrische toestel)
DE ELEKTRONENSTROOMZIN – CONVENTIONELE
STROOMZIN
elektronenstroomzin:
conventionele elektrische stroomzin:
+


+
-
AANDUIDEN VAN EEN GELIJKSPANNING
Een gelijkspanning wordt aangegeven door zijn symbool en zijn waarde,
bij een maatstreep tussen de twee klemmen waar die spanning aanwezig
is. De pijlpunt geeft de positieve klem aan.
10
FARADAY – O HM – P OUILLET
De wet van Faraday
De wet van Ohm
De wet van Pouillet
Q
t
U
R
I
l
R
A
I
S CHAKELEN VAN WEERSTANDEN
SERIE- EN PARALLELSCHAKELING
Serieschakeling
Parallelschakeling
I = I1 = I2 = I3 = ...
I = I1 + I2 + I3 + ...
U = U1 + U2 + U3 + ...
U = U1 = U2 = U3 = ...
Rv = R1 + R2 + R3 + ...
1
1 1
1
    ...
Rv R1 R2 R3
Rv is steeds groter dan de grootste
serie geschakelde weerstand
Rv is steeds kleiner dan de kleinste
parallel geschakelde weerstand
SCHAKELEN VAN TWEE WEERSTANDEN
Rv 
R1  R2
R1  R2
I1  I 
11
R2
R1  R2
I2  I 
R1
R1  R2