Getallenleer ( )

Extra oefeningen wiskunde
3lawe – 3wet
Eerstegraadsfuncties.
Getallenleer
1. Waar of niet waar?
a. Een verband tussen een veranderlijk reëel getal x en een daarmee corresponderend
veranderlijk reëel getal y, waarbij geldt “met elke waarde van x stemt hoogstens
één waarde van y overeen” noemen we een functie in ℜ.
b. Bij een functie noemen we x de afhankelijk veranderlijke en y de onafhankelijk
veranderlijke.
2 .π
is:
2
een rechte evenwijdig met de y–as
een rechte evenwijdig met de x–as
een rechte door de oorsprong
een punt op de y–as
2. De functie met als vergelijking y =
a.
b.
c.
d.
3. Bereken voor de functies in ℜ met onderstaande voorschriften telkens de gevraagde
functiewaarden:
f 5 en f (− 1)
a. y = x 2 + 5
( )
b.
f (0,5) en f (− 3)
y = 2x + 9x + 7x − 6
3
2
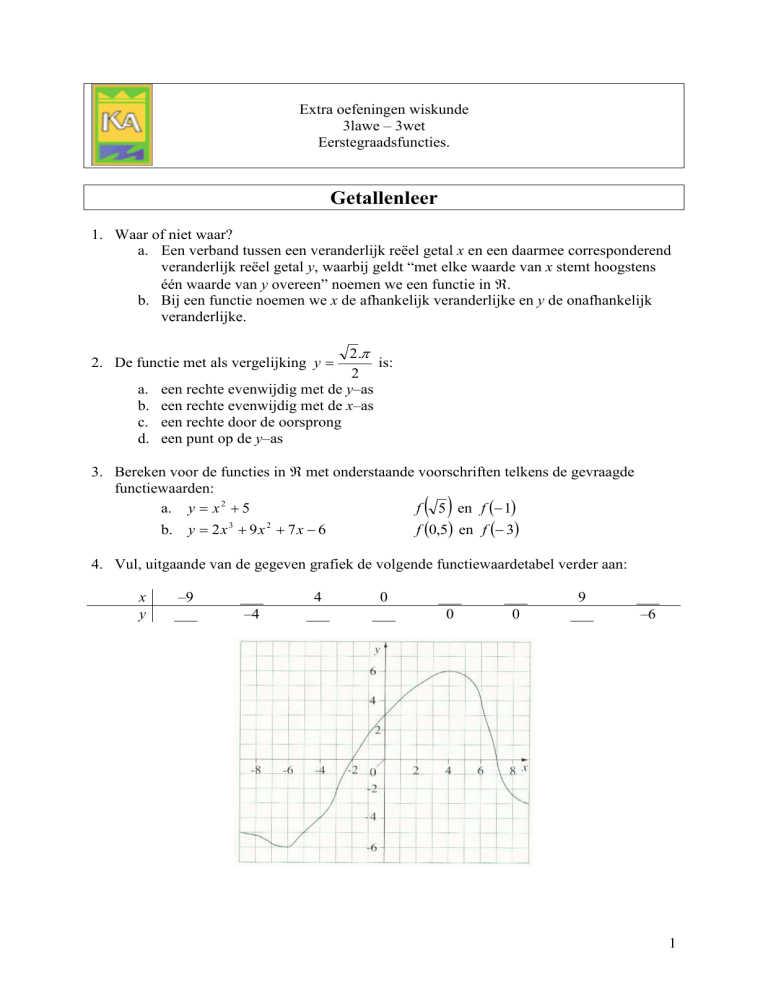
4. Vul, uitgaande van de gegeven grafiek de volgende functiewaardetabel verder aan:
x
y
–9
___
___
–4
4
___
0
___
___
0
___
0
9
___
___
–6
1
1
5. Bepaal van de eerstegraadsfuncties met voorschriften y = 2 x + 5 en y = − x − 1
2
a. stijgend of dalend
b. het snijpunt met de y–as
c. het snijpunt met de x–as
d. de richtingscoëfficiënt
e. domein en bereik
f. het tekenverloop
g. teken de grafiek in het gegeven assenstelsel
6. Bepaal de richtingscoëfficiënt als:
a. f (2) = 5 en f (4) = 8
3
b. y = − x + 2
4
c. 3 x + 5 y − 3 = 0
7. Controleer of de volgende punten liggen op de rechte met als vergelijking
a ↔ −2 x + 3 y − 6 = 0
a. A(0,2)
b. B(− 3,4)
c. C (6,−10)
8. Is AB // CD ?
a. A(1,−1); B(0,−3); C (2,1); D(3,−1)
9. Welke van de volgende rechten met gegeven vergelijkingen zijn evenwijdig?
a. y = −3 x − 8
b. y = −8 x − 3
c. y = 3 x − 8
d. y = −3 x + 4
10. Bepaal de vergelijking van de volgende rechten:
a. door A(1,2) met rico = 2
b. door A(− 2,0) en evenwijdig met y = −2 x + 3
c. door A(2,4) en B(3,2)
d. door de oorsprong en door A(6,3)
3

e. door A 2 ,−  en evenwijdig met de x–as
2

3

f. door A 2 ,−  en evenwijdig met de y–as
2

2
11. Leid uit de volgende tabel het voorschrift van de functie van de bijhorende rechte af:
x
y
–2
4
0
3
1
5
2
4
1
12. Bepaal het voorschrift van de eerstegraadsfuncties waarvan de onderstaande grafieken
gegeven zijn:
3
Oplossingen extra oefeningen wiskunde
3lawe – 3wet
Eerstegraadsfuncties.
Getallenleer
1.
a. waar
b. niet waar
2.
Antwoord b
3.
( 5)=
5 + 5 = 10 en f (− 1) = (− 1) + 5 = 6
2
2
a.
f
b.
f (0,5) = 2.(0,5) + 9.(0,5) + 7.(0,5) − 6 = 0 en
3
2
f (− 3) = 2.(− 3) + 9.(− 3) + 7.(− 3) − 6 = 0
3
2
4.
x
y
–9
–5
–4
–4
4
6
0
3
–2
0
9
–3
7
0
–6
–6
5.
y = 2x + 5
a. a > 0 ⇒ stijgend
b. y = b = 5
b
5
c. x = − = − = −2,5
a
2
d. rico = a = 2
e. dom = ℜ en ber = ℜ
f.
x
–2,5
y
–
0
+
1
y = − x −1
2
a < 0 ⇒ dalend
y = b = −1
b
−1
x=− =−
= −2
a
− 1/ 2
1
rico = a = −
2
dom = ℜ en ber = ℜ
x
y
+
–2
0
–
4
6.
y 2 − y1 8 − 5 3
=
=
x 2 − x1 4 − 2 2
3
b. rico = a = −
4
3
3
3
c. 3 x + 5 y − 3 = 0 ⇒ y = − x + ⇒ rico = a = −
5
5
5
a. rico = a =
7.
a. ⇒ −2.0 + 3.2 − 6 = 0 ⇒ ja
b. ⇒ −2.(− 3) + 3.4 − 6 = 12 ≠ 0 ⇒ neen
c. ⇒ −2.6 + 3.(− 10) − 6 = −48 ≠ 0 ⇒ neen
8.
a AB =
a. a CD =
y 2 − y1 − 3 + 1 − 2
=
=
=2
0 −1
−1
x 2 − x1
y 2 − y1 − 1 − 1 − 2
=
=
= −2
3−2
1
x 2 − x1
a AB ≠ a CD ⇒ niet.evenwijdig
9.
rechte a en rechte d (bij beide rico = a = −3 )
5
10.
a.
y − y1 = a.( x − x1 )
y − 2 = 2.( x − 1) ⇒ y = 2 x
b. a = −2
y − y1 = a.( x − x1 )
y − 0 = −2.( x + 2) ⇒ y = −2 x − 4
y 2 − y1 2 − 4
=
= −2
x 2 − x1 3 − 2
y − y1 = a.( x − x1 )
y − 4 = −2.( x − 2) ⇒ y = −2 x + 8
c. a =
d. oorsprong = (0,0 )
y − y1 3 − 0 1
a= 2
=
=
x 2 − x1 6 − 0 2
y − y1 = a.( x − x1 )
1
1
y − 0 = .( x − 0 ) ⇒ y = x
2
2
3
2
// y − as ⇒ x = c ⇒ x = 2
e. // x − as ⇒ y = b ⇒ y = −
f.
11.
Neem 2 punten uit de tabel: A(− 2,4 ) en B(0,3)
y − y1 3 − 4
1
a= 2
=
=−
2
x 2 − x1 0 + 2
y − y1 = a.( x − x1 )
1
1
y − 4 = − .(x + 2 ) ⇒ y = − x + 3
2
2
6
12.
f) Lees 2 punten af op de grafiek: : A(3,0 ) en B(0,−3)
Snijpunten met assen is het eenvoudigste!
y − y1 − 3 − 0
a= 2
=
=1
x 2 − x1
0−3
y − y1 = a.( x − x1 )
y − 0 = 1.( x − 3) ⇒ y = x − 3
g) Lees 2 punten af op de grafiek: A(1,0) en B(0;2,5)
Snijpunten met assen is het eenvoudigste!
y − y1 2,5 − 0
5
a= 2
=
= −2,5 = −
0 −1
2
x 2 − x1
y − y1 = a.( x − x1 )
5
5
5
y − 0 = − .( x − 1) ⇒ y = − x +
2
2
2
7