Hoofdstuk 1(2)

Analyse deel I: huistaken – groepswerken – opgaven – vragen…
cursus
blz 9
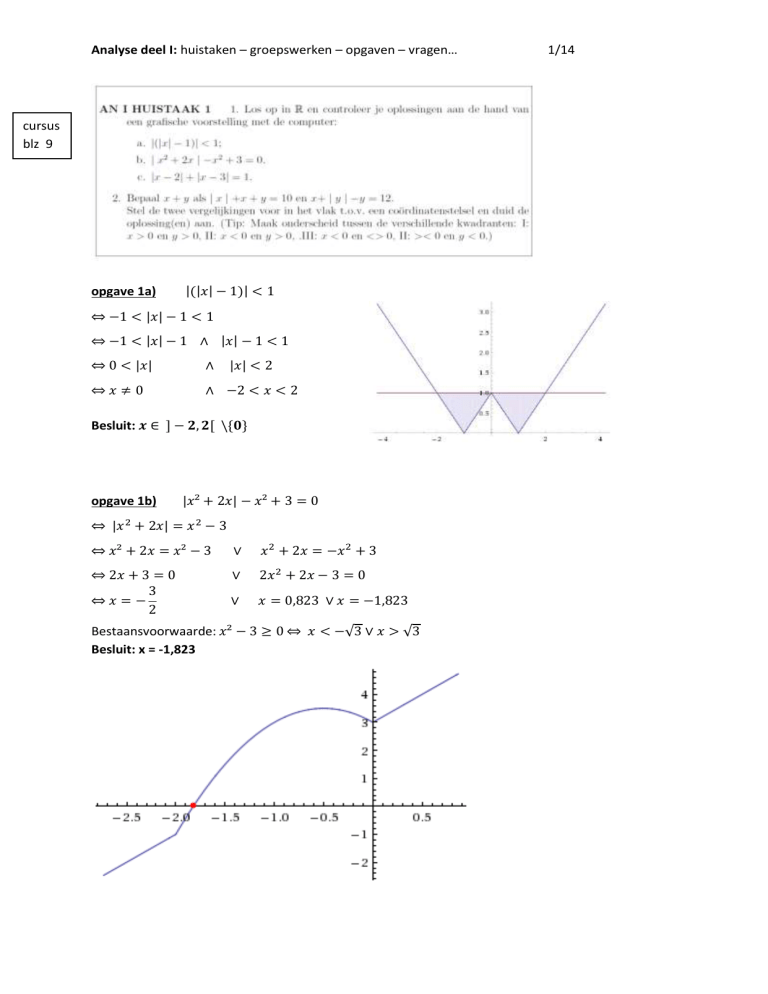
opgave 1a)
|(|𝑥| − 1)| < 1
⇔ −1 < |𝑥| − 1 < 1
⇔ −1 < |𝑥| − 1 ∧ |𝑥| − 1 < 1
⇔ 0 < |𝑥|
∧
|𝑥| < 2
⇔𝑥 ≠0
∧ −2 < 𝑥 < 2
Besluit: 𝒙 ∈ ] − 𝟐, 𝟐[ \{𝟎}
opgave 1b)
|𝑥² + 2𝑥| − 𝑥² + 3 = 0
⇔ |𝑥 2 + 2𝑥| = 𝑥 2 − 3
⇔ 𝑥² + 2𝑥 = 𝑥² − 3
∨
𝑥 2 + 2𝑥 = −𝑥 2 + 3
⇔ 2𝑥 + 3 = 0
3
⇔𝑥 =−
2
∨
2𝑥 2 + 2𝑥 − 3 = 0
∨
𝑥 = 0,823 ∨ 𝑥 = −1,823
Bestaansvoorwaarde: 𝑥² − 3 ≥ 0 ⇔ 𝑥 < −√3 ∨ 𝑥 > √3
Besluit: x = -1,823
1/14
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
opgave 1c)
|𝑥 − 2| + |𝑥 − 3| = 1
x
2
3
x-2 - 0 + + +
x-3 - - - 0 +
𝑥 ≤ 2: − 𝑥 + 2 − 𝑥 + 3 = 1 ⇔ 𝑥 = 2
2 ≤ 𝑥 ≤ 3: 𝑥 − 2 − 𝑥 + 3 = 1 ⇔ 𝑥 ∈ ℝ
𝑥 ≥ 3: 𝑥 − 2 + 𝑥 − 3 = 1 ⇔ 𝑥 = 3
Besluit: 𝒙 ∈ [𝟐, 𝟑]
opgave 2:
2/14
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
3/14
cursus
blz 28
Antwoorden:
1.
ja want voor elke x-waarde is er hoogstens 1 y-waarde, zie voorschrift OK
𝑥−3
𝑥
2.
𝑓: ℝ → ℝ: 𝑥 →
3.
Nee want x=0 heeft geen beeld OK
4.
𝑓: ℝ0 → ℝ\{1}: 𝑥 →
OK
𝑥−3
𝑥
OK
5.
Hier kan je de kenmerken op grafiek vermelden: f is een functie want elke evenwijdige met de y-as
heeft juist één snijpunt met de grafiek uitgezonderd de y-as heeft geen snijpunt.
De functie is injectief want elke evenwijdige met de x-as heeft juist één snijpunt met de grafiek
uitgezonderd de rechte y=1 heeft geen snijpunt met de grafiek.
Enkele vragen bij deze oefening:
Vraag 1:
In nummer 3 antwoord ik met “nee want x=0 heeft geen beeld”, is het ook juist als ik zeg “nee want
y=1 wordt niet bereikt”? Voor een afbeelding gaat het enkel over de pijlen die vertrekken uit de
bron.
Vraag 2:
Het bereik van de functie is ℝ\{1} maar dat heb ik pas gezien in de grafiek. Hoe kan ik dit zien
zonder in de grafiek te spieken?
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
4/14
Antwoorden:
1.
2.
Nee, want elk strikt positief getal 4-x² heeft 2 vierkantswortels. 𝑦 = ±√4 − 𝑥²
twee halve cirkels met straal 2 en middelpunt oorsprong (positieve en negatieve wortel)
Antwoorden:
1.
wanneer géén functie?
-als 𝑢 = 𝑣 = 0, dan moet w=0; grafische voorstelling is de oorsprong
𝑤
-als 𝑣 = 0, dan is 𝑥 = − 𝑢 voor elke y-waarde; grafische voorstelling is een verticale rechte
2.
wanneer wél een functie?
-als 𝑢 ≠ 0 𝑒𝑛 𝑣 ≠ 0 𝑒𝑛 𝑤 = 0 dan heb je een schuine rechte door de oorsprong
- als 𝑢 ≠ 0 𝑒𝑛 𝑣 ≠ 0 𝑒𝑛 𝑤 ≠ 0 dan heb je een schuine rechte niet door de oorsprong
3.
een functie die geen injectie is?
-als 𝑢 = 0 dan heb je een horizontale rechte
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
5/14
Antwoorden:
1.
Dom f = ℝ+ OK
2.
𝑓:ℝ+ → ℝ: 𝑥 → √𝑥 is een afbeelding omdat elk element van R+ een beeld heeft in R. OK
3.
𝑓:ℝ+ → ℝ+ : 𝑥 → √𝑥 OK
4.
Dit is juist want elke x wordt afgebeeld op zijn positieve vierkantswortel. Je kan de grafiek
gemakkelijk tekenen met enkele speciale punten (0,0), (4,2), (9,3) enz. Deze grafiek is een halve
parabool.
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
6/14
Antwoorden:
1.
ja want elk element van R heeft een beeld. OK
2.
geen injectie want f(1)=f(5) => 1=5 en dat kan niet OK
3.
𝑓: ℝ → ℝ: 𝑥 → (𝑥 − 1)(𝑥 − 5) is géén surjectie want het element -5 uit B is niet het beeld
van een element uit A. Hoe heb je dat gevonden?
𝑓: ℝ → [−4, +∞[: 𝑥 → (𝑥 − 1)(𝑥 − 5) is wél een surjectie OK
Antwoorden:
−𝑥 2
2
1.
Ja want 𝑦 =
2.
Nee (2 vierkantswortels…) OK
3.
Ja want 𝑦 = √𝑥 OK
3
OK
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
7/14
cursus
blz 43
Antwoord:
fog=h
⇔
f-1 o (f o g) = f-1 o h
⇔
(f-1 o f) o g = f-1 o h
⇔
g = f-1 o h = … = x²+x-1
Geef het voorschrift van f-1 : x met y verwisselen en oplossen naar y : y=1/3(x-5). Omdat het de
tweede functie is in de samenstelling: f-1 :z=1/3(y-5) en h: y=3x²+3x+2
De samenstelling heeft voorschrift : z=1/3(3x²+3x+2-5)
Jouw antwoord is dus juist maar het is best ook te schrijven hoe je eraan komt.
Antwoorden:
(b)
injectie?
ja want: 𝑓(𝑎) = 𝑓(𝑏) ⇔ 2𝑎3 − 16 = 2𝑏 3 − 16 ⇔ 𝑎 = 𝑏 OK
bijectie?
Ja aan de grafiek is dat makkelijk te zien
VRAAG: hoe zie ik dat aan het voorschrift? Elke x waarde heeft een eigen unieke
derdemacht?
Ja en omgekeerd elke y-waarde is het beeld van juist één x-waarde. Dit is omdat elk
getal slechts één derdemachtswortel heeft. Te zien als je de vergelijking oplost naar x.
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
VRAAG:
cursus
blz 47
Antwoord:
4𝑥 2 + 4𝑦 2 + 4𝑥 + 16𝑦 + 13 = 0
13
⇔ 𝑥 2 + 𝑦 2 + 𝑥 + 4𝑦 +
=0
4
1
13
1
⇔ (𝑥 2 + 𝑥 + ) + (𝑦 2 + 4𝑦 + 4) +
−4− =0
4
4
4
1 2
⇔ (𝑥 + ) + (𝑦 + 2)2 = 1
2
1
verschuiving 𝑣̅ (− 2 , −2) OK
8/14
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
9/14
VRAAG:
cursus
blz 48
Als je een gatal verminderd met 1 dan wordt enkel het geheel gedeelte verminderd met 1, het
decimaal gedeelte blijft behouden. Voor de positieve getallen is dit vrij duidelijk. Voor de
negatieve getallen is -3,156 = -4+0,844
Als we 1 afrekken van het getal dan krijgen we -4,156=-5+0,844
Dus hier ook wordt het geheel gedeelte met 1 verminderd, het decimaal deel blijft hetzelfde.
Deze vraag dient om na te gaan of de betekenis van geheel gedeelte en decimaal gedeelte van een
getal goed is begrepen, vooral voor de negatieve getallen.
VRAAG:
cursus
blz 49
Als ik de vorige vraag snap, dan kan ik deze misschien wel zelf
Deze oefening is in dezelfde zin van de vorige maar steun er niet op.
Je past eerst de verschuiving toe over de vector (2,0) en dan moet het nieuwe voorschrift gelijk zijn
aan het oorspronkelijk voorschrift. (het nieuwe voorschrift vind je door x te vervangen door x-1).
Je stelt deze 2 voorschriften aan elkaar gelijk.
Je vind 2 absolute waarden die gelijk zijn aan elkaar. Dan moeten de getallen gelijk zijn of
tegengesteld.
Door de 2 uitdrukkingen gelijk te stellen, verkrijg je na wat rekenen dat het geheel gedeelte van
(x+1)/2 min het geheel gedeelte van (x-1)/2 moet gelijk zijn aan 1. Dit kan je gemakkelijk zien op de
grafische voorstellingen van geheel gedeelte van (x+1)/2 en van geheel gedeelte van (x-1)/2. Deze
grafische voorstellingen vind je gemakkelijk door de rechten y=(x+1)/2 en y=(x-1)/2 te tekenen en
dan van die beelden het geheel gedeelte te nemen.
De uitdrukkingen aan elkaar tegengesteld stellen, leidt tot een onmogelijkheid: een geheel getal zou
dan moeten gelijk zijn aan een decimaal getal.
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
10/14
VRAAG:
cursus
blz 51
Als K1 en K2 symmetrisch liggen tov de rechte x=2 dan is de ene het beeld van de andere voor de
spiegeling om de rechte x=2.
De transformatieformulles zijn: (x+x’)/2=2 en y’=y (2 is het gemiddelde van x en x’ en de y blijft onveranderd)
Of x=4-x’ en y=y’. We vervangen x en y van K1: 2(4-x’)² + 3y’²=6  dit is de vergelijking van K2.
VRAAG:
cursus
blz 52
𝑦’ = 2𝑏 − 𝑦
(2𝑏 − 𝑦)2 + (2𝑏 − 𝑦) = (𝑦 − 6)2 − 𝑦 + 6
⇔ (2𝑏 − 𝑦)2 + (2𝑏 − 𝑦) = (6 − 𝑦)2 + 6 − 𝑦
⇔ 2𝑏 − 𝑦 = 6 − 𝑦
⇔𝑏 =3
Besluit: tov de rechte y=3 OK
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
11/14
Antwoorden:
(a)
(b)
cirkel met straal 3 en middelpunt (-1,2) OK
(𝑥+1)2
5
2
( )²
+ (𝑦 − 2)2 = 9 Dit is niet juist omdat het middelpunt van de cirkel niet in de
oorsprong ligt. Ook het middelpunt ondergaat een uitrekking. De transformatieformules zijn x’=5/2 x
en y’=y of x=2/5 x’ en y=y’. De vgl wordt: (2/5 x’+1)²+(y-2)²=9. Na uitrekening krijgen we de vgl van
een ellips:
(𝑥+5/2)2
5
2
( )²
+ (𝑦 − 2)2 = 9
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
12/14
(c)
Als je een viertal beelden tekent zou je zien dat de tekening niet juist is. Bepaal dus de
beelden van de 4 bijzondere punten bvb (2,2), (-4,2), (-1,5) en (-1,-1) zijn de beelden resp. (5,2), (-
10,2), (-5/2,5) en (-5/2,-1)
Je ziet dat het middelpunt meer links ligt , de beelden zijn precies de 4 toppen van de ellips.
(d)
(𝑥+1)2
5
( )²
2
+
(𝑦−2)2
1
2
( )²
= 9 dit is niet juist, dezelfde fout als in b)
Het beeld is (𝑥 + 1)² + (𝑦 − 1)2 /4 = 9
(e)
Bepaal dus de beelden van 4 punten.
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
Antwoorden
(a)
(b)
je bekomt weer dezelfde grafiek; het is een even functie OK
10
𝑓(−𝑥) = (−𝑥)2
+4
=
10
𝑥 2 +4
= 𝑓(𝑥)
Antwoorden:
(a)
(b)
10(−𝑥)
+4
Het is een oneven functie: 𝑓(−𝑥) = (−𝑥)2
=−
10𝑥
𝑥 2 +4
= −𝑓(𝑥) OK
13/14
Analyse deel I: huistaken – groepswerken – opgaven – vragen…
14/14
Antwoord
Berekening:
1
5
1
5
( 𝑥(𝑥+5))+(− (𝑥 2 +5𝑥−20))
2
=
𝑥 2 +5𝑥−𝑥 2 −5𝑥+20
10
=
20
10
= 2 OK (volgens de transformatieformules y+y’=4)
Antwoord
Berekening:
aan te tonen: 𝑓(2𝑎 − 𝑥) + 𝑔(𝑥) = 2𝑏 𝑚𝑒𝑡 (𝑎, 𝑏) = (−4,1)
1
1
(−8 − 𝑥)(−8 − 𝑥 + 5) − (𝑥 2 + 11𝑥 + 14)
5
5
1
= 5 [(−8 − 𝑥)(−3 − 𝑥) − (𝑥 2 + 11𝑥 + 14)]
1
= 5 [24 + 11𝑥 + 𝑥 2 − 𝑥 2 − 11𝑥 − 14]
= 2 OK