week 47 - Nikhef

Samenvatting week 10
• analyse van een systeem
 externe kracht versnelt zwaartepunt
 extern koppel leidt tot rotatie
 rotatie en zwaartepuntsversnelling zijn onafhankelijk: 1 kracht kan
zowel het systeem roteren als het systeem versnellen
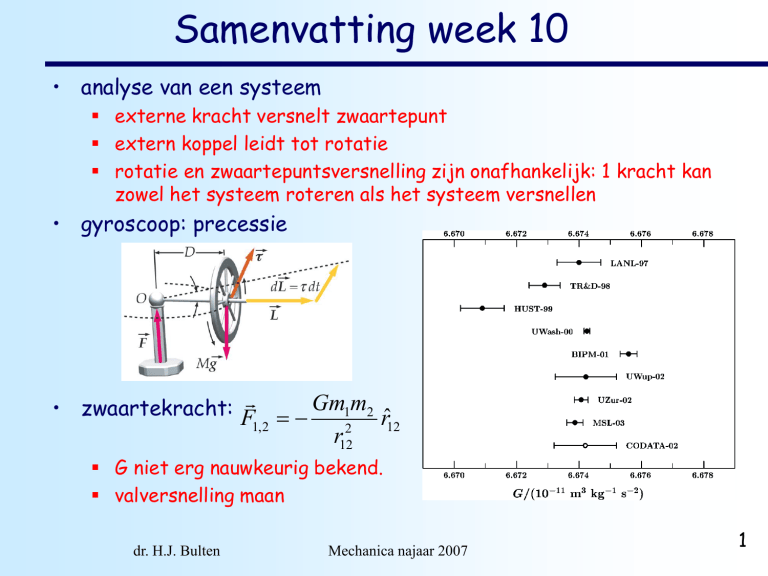
• gyroscoop: precessie
• zwaartekracht: F   Gm1m2 rˆ
1,2
12
2
r12
 G niet erg nauwkeurig bekend.
 valversnelling maan
dr. H.J. Bulten
Mechanica najaar 2007
1
Samenvatting week 10
• wetten van Kepler
 1) ellipsbanen
 2) oppervlakte per
tijdseenheid constant
 3)
2
3
T  cR
• Kepler: fenomenologie
• Newton: bewijs, model
1000
periode [jaar]
 1e hoofdwet volgt uit vorm
zwaartekracht
 2e hoofdwet: behoud
impulsmoment
 3e hoofdwet: uit eerste
twee
omloopsbanen
100
10
1
10
100
1000
10000
0.1
straal [Gm]
dr. H.J. Bulten
Mechanica najaar 2007
2
Gravitatie
• Zwaartekracht: conservatieve kracht.
 potentiaal: U   F ds

r2
r1
dU   F ds   Frˆ ds   Fdr
Gm1m2
dU
 Gm1m2 
 

U
(
r
)

U

0

dr
r2 
r

• op aarde: R bijna constant.
Fzw  
GMm
GMm
ˆ
r


rˆ  mg
2
2
( Re  h)
( Re )
U g ( Re  h)  U ( Re ) 
GMm GMm GMm( Re  h  Re ) GMmh



 mgh
Re
Re  h
Re ( Re  h)
Re2
• integratie constante: vrij te kiezen.
dr. H.J. Bulten
Mechanica najaar 2007
U0  0
Ug  
Gm1m2
r12
3
Gravitatie
• Meestal : keuze dat potentiaal nul is bij oneindige
separatie.
U0  0
Ug  
Gm1m2
r12
• ontsnappingssnelheid:
2GM
ontsnappen: v (r ) 
r
v  Re   2 gRe  11km / s
2
dr. H.J. Bulten
U g  Re   
GMm
Re
K  r   U  r   const
U r    0
ontsnapping : K  r     0
K  r     K  r   U  r   K (r ) 
Mechanica najaar 2007
GMm
r
4
Energiebehoud
• keplerbanen:
1 2
mv
2
GMm
U 
r
GMm
U
v2 2K
F  2  m 
r
r
r
r
U
E  K  U  K 
2
K
 circel : relatie tussen K en U
• Als de kinetische energie groter is
dan -½ U: ellipsbaan
• als de kinetische energie groter is
dan –U : ongebonden.
va  v p
rp
ra
1 1
v  v  2GM   
 rp ra 


2
r
p
rp ra v 2p (1  2 )  2GM (ra  rp )
ra
2
p
2
a
 (ra  rp )ra 
ra
v  2GM 

2
GM
 rp (ra2  rp2 ) 
rp (ra  rp )


2
p
dr. H.J. Bulten
Mechanica najaar 2007
5
Gravitatie veld
• kracht
F1,2  
Gm1m2
rˆ12
2
r12
• veld : kracht uitgeoefend door deeltje 1, gedeeld
door de massa van deeltje 2. Dit veld heeft dus een
richting en is gedefinieerd in een veldpunt P.
g1 
F
m2
• een collectie van deeltjes oefent een gravitatie veld
uit dat de som is van de velden van de individuele
deeltjes. De deeltjes in de collectie worden bronnen
genoemd.
gtot   gi  
i
i
Gmi
rˆ
2 iP
riP
gtot   dg
dr. H.J. Bulten
Mechanica najaar 2007
6
gravitatie veld
• twee puntdeeltjes:
 veld langs x-as:
GM
r2
GM
g1, x  g 2, x  2 2 cos 
r
GM
g1, y  g 2, y  2  sin   sin    0
r
x
x
cos   
r
x2  a2
g1  g 2 
g ( x)  
2GMx
xˆ
( x 2  a 2 )3/ 2
dr. H.J. Bulten
Mechanica najaar 2007
7
staaf, veld in lengterichting
• staaf:
 volume deeltje dm
dg x ( x0 ) : dm 
dg x  
M
dx, r  ( x0  x)
L
GM
dx
2
L( x0  x)
L/2
GM
GM  1 
GM
g x   dg x   
dx






L( x0  x) 2
L  x0  x   L / 2
L
L/ 2
GM

2
L
2
x0   
2
L/2
dr. H.J. Bulten
Mechanica najaar 2007


1
1



x

L
/
2
x

L
/
2
0
 0

8
Bol, bolschil
• Newton: integraalrekening
• Fysica: interacties: veld in ruimte
 quantummechanica: interacties van velden (potentialen) op
golffunctie
 Electrodynamica: ladingen en stromen bepalen E.M. veld in
ruimte, EM veld beschrijft EM verschijnselen.
• Bolschil:
 GM
 2 rˆ, r  R
g r
 0, r  R
2
1
2
2
m1 r

m2 r
dr. H.J. Bulten
Mechanica najaar 2007
9
Bolschil
• eerst: beschouw contributie van een ring
dg x   dg cos   
Gdm
cos 
s2
M
M
M
2
dA 
2

R
sin

d


sin  d
A
4 R 2
2
GdM
M sin  d
dg r   2 cos   
cos 
s
2s 2
s 2  r 2  R 2  2rR cos 
dm 
d 2
ds
s  2s
 2rR sin 
d
d
R 2  s 2  r 2  2 sr cos 
dr. H.J. Bulten
sds
rR
s2  r 2  R2
 cos  
2 sr
 sin  d 
Mechanica najaar 2007
10
Bolschil
M sin  d
cos  
2
2s
GM  sds   s 2  r 2  R 2 
 2 


2 s  rR  
2sr

dg r  


GM
2
2
2
s

r

R

2 2
4s r R
GM  r 2  R 2 
 2 1 
 ds
4r R 
s2 

rR
GM
 (r  R)(r  R) 
g r   2  1 
ds 
2
4r R r  R 
s

rR
GM  (r  R)(r  R) 
GM
  2 s 



4r R 
s
r2
rR
dr. H.J. Bulten
Mechanica najaar 2007
11
Bol
• Bol: het resultaat van een
bol kan worden bereikt
door bolschillen bij elkaar
op te tellen.
• veld in homogene bol:
alleen het deel bij
kleinere straal levert
netto veld.
dr. H.J. Bulten
GdM
rˆ (r  R )
r2
G
GM
Bol : g   2  dM   2
(r  R)
r
r
Schil : dg  
r3
M  M 3
R
GM 
GM
g   2   3 r (r  R )
r
R
Mechanica najaar 2007
12
bol-symmetrisch
• Voorbeeld Bol: dichtheid neemt lineair toe met de
straal.
R
R
M   4 r dr   4 r 2Crdr  C R 4
2
0
C
0
M
 R4
g (r ) 
rschil

0
4 r 3C
G
G 2
dr   2
rschil
rschil
dr. H.J. Bulten
rschil

0
2
GMrschil
4 r Cdr  
R4
3
Mechanica najaar 2007
13
Bespreking tentamenopgaven
dr. H.J. Bulten
Mechanica najaar 2007
14