Week 1: introductie

Samenvatting week 11
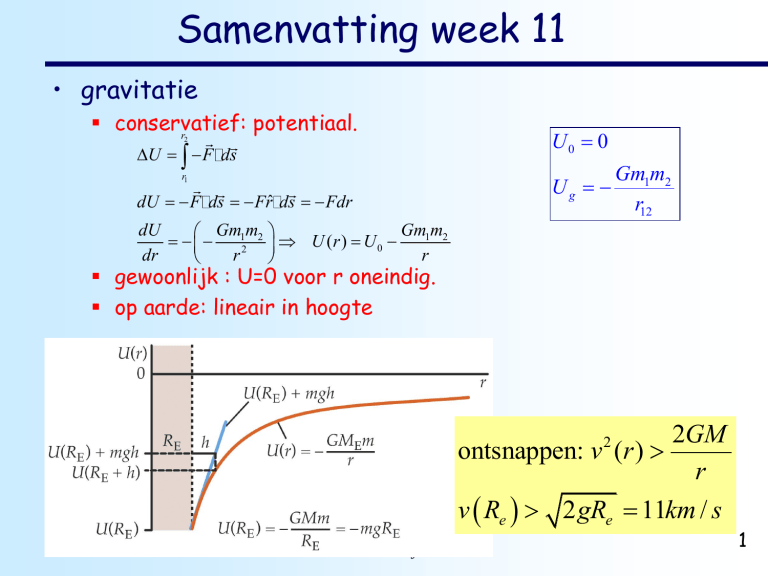
• gravitatie
 conservatief:
potentiaal.
r
U0  0
2
U    F ds
Ug  
r1
dU   F ds   Frˆ ds   Fdr
Gm1m2
r12
Gm1m2
dU
 Gm1m2 
 

U
(
r
)

U

0

dr
r2 
r

 gewoonlijk : U=0 voor r oneindig.
 op aarde: lineair in hoogte
2GM
ontsnappen: v (r ) 
r
v  Re   2 gRe  11km / s
2
dr. H.J. Bulten
Mechanica najaar 2007
1
Gravitatie veld
• veld : kracht uitgeoefend door deeltje 1, gedeeld
door de massa van deeltje 2. Dit veld heeft dus een
richting en is gedefinieerd in een veldpunt P. g  F
1
m2
• resultaten voor 2 puntdeeltjes, staaf, bolschil, bol
 bolsymmetrische schil: veld 0 binnen schil, veld als van
puntdeeltje in zwaartepunt buiten bol.
 GM
 2 rˆ, r  R
g r
 0, r  R
dr. H.J. Bulten
Mechanica najaar 2007
2
bol-symmetrisch
• Voorbeeld Bol: dichtheid neemt lineair toe met de
straal.
R
R
M   4 r  dr   4 r 2Crdr  C R 4
2
0
C
0
M
 R4
r
G
GMr 2
2
g (r )   2  4 r Crdr  
r 0
R4
dr. H.J. Bulten
Mechanica najaar 2007
3
Evenwicht
dr. H.J. Bulten
Mechanica najaar 2007
5
Evenwicht : uitgebreide lichamen
• Netto externe kracht moet nul zijn: dpdt   F  0
• Netto extern koppel rond willekeurig punt moet 0
zijn:   0
• Zwaartekracht: grijpt aan in
zwaartepunt
CM
  rcg  W


 net   mi ri  g    mi ri   g  MrCM  g  rCM  W
i

i

• Hier is aangenomen: zwaartekracht
uniform over volume object.
dr. H.J. Bulten
Mechanica najaar 2007
6
Evenwicht
• zwaartepunt: te bepalen door
ophanging.
• Voorbeeld: plank:
• Wat lezen de weegschalen uit?
Hoe zwaar kan Marie zijn
zonder dat de plank kantelt?
dr. H.J. Bulten
Mechanica najaar 2007
7
voorbeeld: plank
• 1) vrijelichaamsdiagram
• 2) externe kracht 0
mg  Mg  FL  FR  0
FL  FR  (m  M ) g
• 3) extern koppel 0
• Kies punt om koppel uit te
rekenen! Kies richting
  Fr ( L  2d )  Mg
L  2d
 mgd
2
• stel gelijk aan 0:
d
1

Fr   M 
m g
L  2d 
2
dr. H.J. Bulten
• vul FR in in 2) om FL uit
te rekenen:
FL  FR  (m  M ) g
Ld 
1
FL   M 
m g
L  2d 
2
• FR=0 ->
Mechanica najaar 2007
m
L  2d
M
2d
8
Voorbeeld: bord
• Bord: 20 kg.
• staaf : 4 kg
• dus ook vertikale kracht
in punt O!
Fy  Ty   M  m  g
Fx  Tx  0
tan  
1
2
TL sin   MLg  m
L
g  0  T  483 N
2
F  432 Nxˆ  19 Nyˆ
dr. H.J. Bulten
Mechanica najaar 2007
9
Voorbeeld : wiel
• Als je naar voren duwt, hoe
hard moet je duwen om
over een drempel te gaan?
• richting kracht drempel
niet bekend: kies
aangrijppunt drempel om
koppel te berekenen!
wiel omhoog: Fn  0
  0
 Fmin ( R  h)  Mgx
x  R 2  ( R  h) 2   h 2  2hR
Fmin  Mg
h(2 R  h)
Rh
dr. H.J. Bulten
Mechanica najaar 2007
10
voorbeeld: ladder
• Wanneer gaat een
ladder glijden?
 s ,min 
fs
Fn
Fn  w
  (4m) F1  (1.5m) w
F1 
90
N  fs
4
• Fn en w, en fs en F1 zijn even
groot en tegenovergesteld:
krachtenpaar
dr. H.J. Bulten
Mechanica najaar 2007
11
Krachtenparen
• Krachten zoals Fn en w zijn even groot en
tegenovergesteld in richting: geven een vast koppel
t.o.v. ieder punt.
  r1  F1  r2  F2  (r1  r2 )  F
  FD
dr. H.J. Bulten
Mechanica najaar 2007
12
evenwicht in versnelde stelsels
• evenwicht: alleen C.O.M versnelling:
F
ext
 macm

cm
 I cm  0
Fn  mg
f s  ma
h
 Fn d  0
2
h
L
L
ma  mg  0  amax  g
2
2
h
 cm  f s
dr. H.J. Bulten
Mechanica najaar 2007
13
Stabiliteit van rotationeel evenwicht
• Stabiliteit: als bij kleine rotatie een koppel ontstaat
om de rotatie ongedaan te maken: stabiel
• als het koppel de rotatie versnelt: labiel, instabiel
• als er geen extra koppel ontstaat: neutraal
• stabiel: zwaartepunt gaat omhoog bij verplaatsing
dr. H.J. Bulten
Mechanica najaar 2007
14
evenwicht
stabiel: zolang het
zwaartepunt zich boven
de basis bevindt
Ook de grootte van het
terugdrijvende koppel is
groter voor een
bredere basis
dr. H.J. Bulten
Mechanica najaar 2007
15
Materiaaleigenschappen
• Stress (spanning) ,
strain
• kleine kracht:
evenredig (veerwet,
Hooke’s law)
• iets grotere kracht:
elastische vervorming
Strain :
dr. H.J. Bulten
Mechanica najaar 2007
L
L
stress :
F
A
16
Young’s modulus
• ratio tussen stress en strain voor een materiaal in
het lineaire gebied: Y  F / A
L / L
dr. H.J. Bulten
Mechanica najaar 2007
17
Draaiing: shear forces
Fs
A
x
Shear strain :
 tan 
L
Shear stress :
dr. H.J. Bulten
Mechanica najaar 2007
18