lessen over energie - digitaal zelfportret

ARBEID & ENERGIE
1
WERELD ENERGIE PROBLEEM
2
ARBEID EN ENERGIE
3
REKENEN AAN ENERGIE
4
SJOELEN
5
EXTRA SOMMEN
Co BTn
WEP
WEP
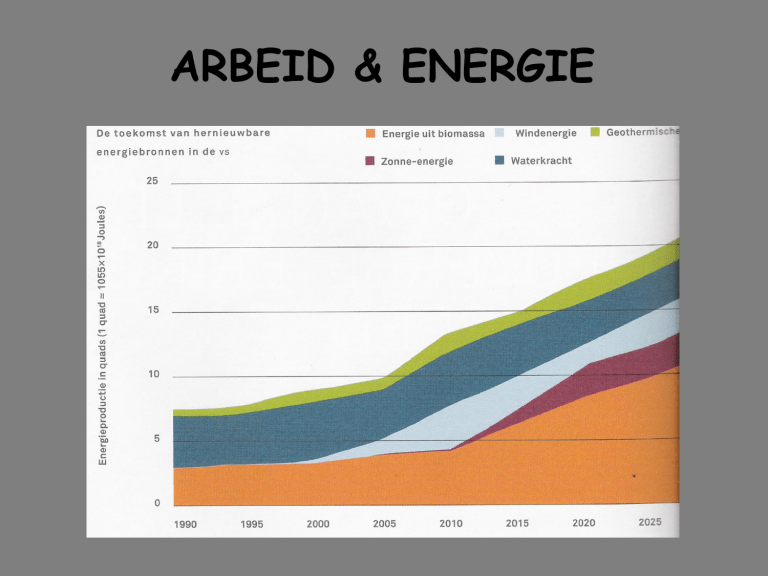
1 WERELD ENERGIE PROBLEEM
CLUB VAN ROME
1972 GRENZEN AAN DE GROEI
Dennis Meadows: modeldenken
5 variabelen: zie figuur
Ineenstorting wereldsysteem
Voorspellingen kwamen niet uit:
Modellen veel en veel te simpel
ENERGIE-PROBLEEM
Sites energie bedrijven
http://www.energyvalley.nl/
http://www.ecn.nl
http://www.energie.nl/
Sites actiegroepen
http://www.milieudefensie.nl/
http://www.greenpeace.nl/
http://www.milieucentraal.nl/
Fossiele brandstoffen
CARBOON
(360-286 x106).
Moerassen met
afstervend leven
wordt GAS, OLIE en STEENKOOL
GEOLOGIE = wetenschap van de
(geschiedenis van de) aarde
Talloze ijstijden en zeespiegelstijgingen 
Nieuwe lagen bovenop organisch materiaal 
Olie en gas ingepakt onder afsluitende lagen
Fossiele brandstoffen: olie
Voordelen
• Goedkoop
Nadelen
• Sterk broeikaseffect
• Hoge milieubelasting bij winning
• Afhankelijk regio (Midden Oosten)
• Raakt op
• Steeds moeilijker winbaar
Fossiele brandstoffen:gas
Voordelen
Goedkoop
Nadelen
Broeikaseffect
Sterk afhankelijk van MO
Raakt op
Steeds moeilijker winbaar
1959 ontdekking aardgasbel bij Slochteren 
Nederland werd energie-exporterend land 
enorme opbrengst (ca 150 miljard euro)
Na ontdekking
Slochteren 1000den km
pijpleiding in Nederland
aangelegd
Fossiele brandstoffen: kolen
Nederland slot zijn mijnen in 1965,
Minister Joop Den Uyl
Voordelen
•
Goedkoop
•
Enorme voorraden
•
Onafhankelijk van een regio
Nadelen
•
Zeer sterk broeikaseffect
•
Hoge milieubelasting bij winning
zonne-energie
zonnecellen
californie
Voordelen
• Schoon
• Raakt nooit op
• Onafhankelijk
Nadelen
• Duur
• Gering vermogen
• Verpest landschap
2 soorten techniek
1 Zonnecellen op dak
(duur, lokaal)
2 Concentrated Solar Power
(goedkoop, centraal)
frankrijk
australie
Hydraulische energie
14 MW LINNE MAAS
Voordelen
• Schoon
• Raakt nooit op
• Onafhankelijk
Nadelen
• Duur
• Gering vermogen
• Verpest landschap?
Wind energie
Voordelen
• Schoon
• Raakt nooit op
• Onafhankelijk
Nadelen
• Rendementsprobleem
• Duur
• Gering vermogen
• Verpest landschap?
Kernsplijting
90
143
1
n  235
U

Kr

Ba

3
92
38
54
0n
1
0
Borsele
Voordelen
• Kernenergie is goedkoop
• Onafhankelijk Midden-Oosten
• Produceert geen broeikasgassen
Dodewaard
Nadelen
• Radioactief afval als restproduct
• Eeuwenlange bewaking
Kernfusie (ITER Frankrijk)
Voordelen
• Geen broeikasgas!
• Waterstof onuitputtelijk
• grote hoeveelheden energie
Nadelen
• Winning erg duur
• Zit nog in ontwikkeling fase
Gegevens van ITER
Totale hoogte: 24 meter
Totale doorsnede: 30 meter
Plasmastroom: 15 - 17 mega-ampère
Hoofdstraal tokamak: 6,2 meter
plasmastraal: 2,0 meter
toroïdaal magneetveld op de as: 5,3 tesla
Levensduur plasma: 500 tot 1000 seconden
Energievermenigvuldigingsfactor: 10
Nominaal fusievermogen: 500 - 700 megawatt
Bouwkosten: 5 miljard euro
http://www.fusie-energie.nl/
Brandstofcel
Voordelen
• Geen afvalstoffen
• Geen fossiele brandstof nodig
• Werk ook op methanol
Nadelen
• Katalysator Platina duur
• Waterstof productie kost veel energie
Biomassa
1 Vergisting
2 Vergassing
3 Pyrolyse
4 Verbranding
5 Bio-olie
Voordelen
• Geen broeikaseffect
• Geen afvalstoffen
• Duurzaam
Nadelen
• Ruimtebeslag
• Arbeidsintensief dus duur
Aardwarmte
Voordelen
. Geen afval stoffen
. duurzaam
Nadelen
. Centrales kan bij ons niet
(wel 40.000 warmte pompen)
. Dure installaties
stoomafval
Trends volgens Al Gore
Nieuw: winning uit schalie
Schalie voorraden plenty!
ARBEID & ENERGIE
2
ARBEID EN ENERGIE
spiekbriefje
def arbeid
W=F.Δs
def energie
vermogen om arbeid te verrichten
1e hoofdwet (E-behoud) Evoor = Ena
2e hoofdwet (warmte)
bij elk proces is warmteverlies
Etotaal
Enuttig + Q
vermogen
P=W/t
def rendement
η = (Enuttig / Etotaal).100%
Kinetische
Zwaarte
Veer
Warmte
Energie
Energie
Energie
Q = Fw. Δs
Ekin = ½ mv2
Ez= mgh
Eveer = ½cu2
Definitie arbeid
rolschaatsen gaat van zelf
 geen ARBEID
Een massa optillen kost moeite
 wel ARBEID
En wel meer moeite naarmate
(1) Kracht F groter is
(2) Afstand Δs groter is
Definitie arbeid
Kracht F die verplaatsing Δs veroorzaakt verricht arbeid W = F.Δs
Vbn 1
VERHUIZEN
piano optillen naar 4e verdieping van grachtenpand m = 500 kg, h = 15 m.
Fz = m.g
 Fspan = Fz = 500 (kg) x 10 (N/kg) = 5 000 (N)
Wz = Fz.h
 Wz= 5 000 (N) x 15 (m) = 75.000 (Nm)
 Wz = 75 . 000 (Joule ) = 75 (kJ)
Fietsen en Hardlopen
Vbn 2 FIETSEN
Bij fietsen moet je arbeid leveren om de (lucht en rol)wrijving te
overwinnen. Stel dat deze wrijving 15 (N) bedraagt
A Hoeveel arbeid kost dan een ritje van 10 km?
Wfietsen =F.Δs =15 (N).10.000 (m) = 150.000 (Nm of J) = 150 (kJ)
Vbn 3 HARDLOPEN
Hardlopen is vooral zwaar omdat je je lijf elke stap moet optillen: stel dat
je de 10 km holt in stappen van 80 cm en dat je lijf van 60 kg elke stap 10
cm moet worden opgetild. Gegeven is dat een broodje kaas 200 kJ levert.
A Hoeveel arbeid kost dan die 10 km?
Wstap=F.Δs =600 (N).0,10 (m) = 60 (J)
dus W10 km= n.Wstap=(10.000/0,80)x60 =12.500x60 = 750 000 (J)=750 (kJ)
B En nu als je ook nog een constante tegenwind van 10 (N) ondervindt?
Wwind=F.Δs =10 (N)x10.000 (m) = 100.000 (J)=100 (kJ)
dus W lopen = W10km +Wwind= 100 +750 =850 (kJ)
C Hoeveel broodjes kaas kosten die 10 km?
Dat worden er 850 /200= 4,25, even meer dan 4 dus!
Vermogen
W
P
t
Of je moe wordt van hardlopen of fietsen hangt af van de tijd die er
voor nodig is. Wie veel vermogen moet leveren krijgt hartkloppingen!
Definitie VERMOGEN P
Het vermogen is de arbeid die er per seconde verricht wordt
Vbn 4 DE HARDLOPER EN DE FIETSER
Een snelle fietser doet de 10 km in 1000 sec een langzame in 3000 sec.
Zoals je weet kost 10 km fietsen 150 kJ.
A Bereken voor beide fietsers het geleverd vermogen in Watt (J/s).
Psnel 
150.000( J )
150.000(J)
 150(W ) Ptraag 
 50(W)
1000( s)
3.000(s)
Een snelle loper doet de tien km in 40 minuten, een langzame in 60
minuten. Je weet nog dat 10 km hollen 850 kJ kost?
B Bereken voor beide lopers het geleverd vermogen in Watt (J/s).
Psnel 
850.000( J )
850.000(J)
 354(W ) Ptraag 
 236(W)
40 x60( s)
60x60(s)
definitie energie
met ENERGIEBRONNEN
Hout
Kolen
Gas
Olie
Zon
Atoom
Wind
Water Plant
kun je machines laten werken!
Definitie ENERGIE
Energie is het vermogen arbeid te verrichten
Ech
 W +
Q
Energie  Arbeid + Warmte
Vbn 5 WARMTEMACHINE
Met bovenstaand warmte machine (rendement van 25%) wordt een massa van
200 kg over 10 m opgetild.
A Hoeveel chemische energie zat er in de energiebron?
W=F.Δs=2000 (N).10(m) = 20 000 (J) = 20 (kJ)
Rendement 1/4 dus Ech =4.W =4.20(kJ)=80(kJ)
B De bron was olie (20 MJ/kg): hoeveel gram olie is er gebruikt?
1 kg levert 20 MJ dus 1 gr levert 20 kJ
Nodig is dus 80/20 = 4 gram olie
Perpetuum mobile
CAPILLAIRE WERKING
Glas trekt water aan 
Water kruipt omhoog in buisje 
Bochtje om: kraan druppelt 
Turbine draait en levert elektriciteit
DYN
Wat is de fout !?!?!?
??? 
1830
E elek
PM bestaat niet
PERPETUUM MOBILE = eeuwige beweger
energie lijkt uit het niets te ontstaan

Inzicht in Energie-behoud
WET VAN BEHOUD VAN ENERGIE
(1) Machines hebben brandstof nodig
(2) Energie kan nooit zo maar ontstaan of verdwijnen
(3) Bij elk proces geldt Evoor = Ena
Perpetuum mobile in soorten en maten
Vbn 6Wat is het idee en wat is de fout?
Rendement η

E nuttig
Etotaal
Niet alle energie die je tot je beschikking hebt is nuttig te gebruiken. Vaak
is er maar een bepaald deel nuttig. Denk aan je bromfietsbenzine: een deel
wordt verslingerd aan het verwarmen van je motorblok, dat is niet nuttig.
Echemisch  Wbrommer + Q
benzine  arbeid + warmte
Definitie RENDEMENT
Het rendement van een machine is het nuttig deel van de verbruikte energie
Vbn 7 BROMMER RIJDEN
Een brommer ondervindt een wrijving van 150 N. In een liter benzine zit 30
MJ aan energie. Het rendement van de motor is 10 %.
A Hoeveel arbeid verricht de motor met 1 liter benzine?
Rendement 10%  Wbrommer = 0,10xEchemisch = 0,10x30 = 3 (MJ)
B Hoeveel km rijdt zo’n brommer dus op 1 liter?
W = FxΔs  afgelegde weg Δs = W/F
 Δs = 3 000 000 (Nm)/ 150 (N) = 20.000 (m) = 20 (km)
Zwaarte-energie
Ez = mgh
Vbn 8 WITTE STEENKOOL
In België heb je heel veel stuwmeren waar men
de zwaarte-energie van water in elektrische
energie omzet, door het water op turbines te
laten vallen. In Robertville valt er per seconde
100 m3 water vanaf 60 m hoogte omlaag.
Gegeven: ηcentrale = 25%, ρwater = 1000 kg/m3.
A Hoeveel zwaarte-energie wordt er per seconde gebruikt?
vallende watermassa per seconde m = 100 x 1000 = 1,0 x 10 5 (kg/s)
zwaarte energie Ez = m.g.h = 1,0x105 (kg/s)x10(m/s2)x60 (m)
dus beschikbaar is Pz = 6,0 x 107 (J/s) = 60 (MW)
B Hoeveel elektrische energie ontstaat daar er per seconde in de centrale?
Rendement 25%  Pelek = 0,25. Pzwaarte = 0,25 x 60 = 15 (MW)
C Hoeveel 40 W lampen kunnen er tegelijkertijd op deze centrale branden?
Veel: 15.000.000 / 40 = 375.000 lampen tegelijkertijd
Kinetische energie
Ekin =½mv2
Vbn 9 WINDMOLENS
Overal in Noord-Holland staan windmolens,
die de kinetische energie van lucht omzetten
50
in elektrische energie. De getekende cilinder
m2
gaat in 1 seconde door wiekoppervlak A.
Gegeven: vwind = 12 m/s, wiekopp. A = 50 m2,
12 m/s
ρlucht = 1,3 (kg/m3) en ηmolen = 20%.
A Bereken de massa van de lucht in de getekende cilinder.
V = h . A = 12 (m) x 50 (m2) = 600 (m3)
m = ρ . V = 1,3 (kg/m3) x 600 (m3) = 780 (kg)
B Hoeveel Joule is er per seconde beschikbaar aan kinetische energie?
Elke seconde geeft zo’n cilinder lucht de kinetische energie af:
Ekin = ½mv2 = ½.780 (kg) . 122 (m2/s2) = 56.160  56 x103 (J)
C Hoeveel elektrisch vermogen ontstaat hieruit?
Rendement 20%  Pel = 0,20 Pkin = 0,20 x 56 = 11,2 (kJ/s oftewel kW)
Veer-energie
Eveer = ½cu2
In een katapult zit veer-energie, je kunt er projectielen mee wegschieten.
Hoe snel die uiteindelijk gaan hangt af van de sterkte van de veer en van
de massa van het projectiel .
Definitie VEERSTERKTE c= F/u
De sterkte van een veer is de kracht nodig voor een rek van 1 meter
Vbn 10 KATAPULT
Het 80 cm uitrekken van een katapult kost
160 N. Met de katapult wordt een steentje
van 20 gram weggeschoten.
A Bereken de sterkte van de veer.
c = F / u = 160 (N) / 0,80 (m) = 200 (N/m)
B Bereken de veerenergie van de katapult.
Eveer=½cu2= ½.200.0,82 = 64 (J)
C Toon aan dat de beginsnelheid van het steentje 80 m/s is.
Eveer  Ekin dus 64 = ½mv2 = ½0,020 v2  v2 = 6400  v = 80(m/s)
D De steen raakt 30 m hoger het raam, bereken met welke snelheid dat is.
Omzetting opstijgen: Ekin  Ekin’+ Ez dus ½mv2 =½mw2 + mgh
w2 = v2 – 2.g.h = 802 – 2.10.30 = 6400 – 600 =5800 dus w = √5800 = 76 m/s
Warmte
Q = Fw. Δs
Bij bijna alle natuurkundige processen treedt wrijving op, er ontstaat warmte.
Warmte is de arbeid van de wrijvingskracht op remweg Δs, Q = Fw.Δs
Vbn 11 AQUA VITE!
In pretpark Duinrell in Wassenaar staat de attractie Aqua Vite, waarvan je
net een foto zag. Zeg dat je vanaf 6,0 m hoogte met je boot over een met
water besproeide baan langs een 10 m lange baan omlaag glijdt. Daarna kom
je in de rembak na 4 m tot stilstand. Je massa is 60 kg (met boot en al!).
A Bereken de snelheid beneden als er geen wrijving op de baan zou zijn.
Wrijvingsloos omlaag: Ez  Ekin dus mgh = ½mv2  v2 = 2.g.h
 v = √2gh = √2x10x6 = √120 = 10,9 (m/s)
Die snelheid is te hoog: er was wel wrijving op de helling namelijk 100 N
B Bereken opnieuw de snelheid beneden aan het begin van de waterbak
Met wrijving is de omzetting: Ez  Ekin + Q dus mgh = ½mw2 + FΔ.s
60.10.6 = ½.60.w2+100.10  3.600 = 30w2 +1.000  w = √(2600/30) = 9.4 (m/s)
C Bereken uit deze lage snelheid de remkracht van het water op het bootje.
Omzetting bij remmen: Ekin  Q dus ½mw2 = Fw Δs.
Invullen: ½.60.9,42 = Frem . 4  2.600 = Frem.4  Frem = 650 (N)
Zwaarte-energie
Hoeveel energie bezit massa m op hoogte h ?
Stel dat een verhuizer de massa via een katrol
optilt, dan wordt de arbeid van de spankracht
die de verhuizer levert omgezet in zwaarteenergie:
W  Ez
Dus
Ez = Fspan . Δs
Volgens de traagheidswet zijn de spankracht
en de zwaartekracht gelijk,
Ez = Fz .h,
dus
Ez = m.g.h!
Ez=mgh
kinetische energie Ekin = ½mv2
kinetische energie
v
m
Ekin W 
Ekin  F .s 
Ekin  m .a .s 
Ekin  m . v .s 
 t 
Ekin  m .v . s  
 t 
Ekin  m .v .vgem 
Ekin  m .v . 21v 
Ekin  21 mv 2
remarbeid
vgem
Frem
remweg Δs
definitie arbeid
tweede wet van Newton: F=m.a
definitie versnelling
volgorde vermenigvuldigen en delen
definitie gemiddelde snelheid
helft van topsnelheid
Veer-energie
Eveer =½cu2
Fduw
Fduw
u
Fmax
u
Als je een veer induwt dan is er energie in opgeslagen, want zo ‘n veer kan
een massaatje wegschieten (katapult). De opgeslagen veerenergie is gelijk
aan de geleverde arbeid tijdens het induwen, de oppervlakte onder de grafiek:
Wduw  Eveer
dus
Eveer = <Fduw>.u
Eveer = ½Fmax.u
Eveer = ½.cu.u
Eveer = ½cu2
ARBEID & ENERGIE
3 REKENEN AAN ENERGIE
Sommen maken met energie
Met energieomzettingen zijn veel problemen op te lossen:
Een projectiel verlaat het kanon met snelheid v = 100 m/s, om
op hoogte h = 100 m een vijandelijke helikopter met onbekende
snelheid w te treffen. Hoe groot is die snelheid w?
1 plaatje met gegevens maken
2 energie-omzetting opschrijven
Bij het opstijgen vermindert Ekin omdat Ez stijgt. Dus
Ekin  Ez + Ekin
beneden
boven
3 formule maken met E-behoud
½mv2 = mgh +½mw2
w
massa wegdelen en x 2
v2= 2gh + w2
4 en reken dan uit wat je nodig hebt
w2= v2 – 2gh
v
Invullen levert
w = √(1002 – 2x10x100) = √8.000 = 89,4 m/s
I
DIVERSE WORPEN
A
Van top van de toren tot het hoogste punt vermindert de
kinetische en vermeerdert de zwaarte-energie, dus
E kin  E z  E z ' E kin
1
2
w
mv 2  mgh  12 mw2  mgH  (x2, gedeeld door m)
v 2  2 gh  w 2  2 gH  (invullen)
v
20  2 x10 x 45  w  2 x10 x60
2
2
H
400  900  1300  w  1200 
2
h
w  100  10(m / s )
B
Van top tot bodem wordt alles kinetische energie, dus beide
eindsnelheden zijn gelijk, namelijk
E kin  E z  E kin
1
2
mv 2  mgh  12 mw 2 
v 2  2 gh  w 2
v
h
w 2  20 2  2 x10 x 45  1300 
w  1300  36,1(m / s )
ww
II MET PIJL EN BOOG SCHIETEN
A Sterkte boog
F
350N
c 

 437,5  4,4x 102 (N / m )
u
0,80m
B Opgeslagen veer-energie
1
Eveer  21 cu 2  438x 0,82  140(J )
2
C Helft hiervan wordt kinetische energie, dus
1
E kin  70(J )  21 mv 2  x 0,200xv 2  v 2  700  v  700  26,4(m / s )
2
D De kinetische energie van de pijl wordt omgezet in zwaarte-energie,
E kin
1
v2
26,42
2
2
 E z dus mv  mgh  v  2 gh  h 

 34,8(m )
2
2 g 2x 10
E Bij het opstijgen vermindert de kinetische energie omdat de zwaarteenergie groeit,
E kin  E z  E kin dus
1
2
mv 2  mgh  21 mw 2 
w 2  v 2  2 gh  26,4 2  2x 10x 20  297  w  17,2(m / s )
III
MAFFE VISSEN
A
Het vernietigen van de boot door de vis is
te zien als het omzetten van kinetische energie in
warmte, je kunt de remkracht berekenen uit de
deukdiepte via de energie-omzetting:
E kin  Q dus
1
2
mv 2  Frem s 
0,5 x 200 x112  Frem x0,80 
1.210  0,80 Frem  Frem  1.2100 / 0,80  1.5 x10 4 ( N )
B
Voor het remmen van de vis door het
koord geldt dezelfde omzetting:
Ekin  Q dus
1
2
mv2  Frem s 
0,5 x10 x112  800 xs 
605  800 xs  s  605 / 800  0,76(m)
IV AQUA VITE
A Bij het omlaag glijden zonder wrijving wordt zwaarte-energie in
kinetische energie omgezet
E z  E kin dus mgh  21 mv 2 
v 2  2 gh  2x 10x 8  160 
w  160  12,6(m / s )
B Met wrijving ontstaat er op de helling warmte zodat de kinetische
energie en dus de snelheid lager uitkomen
E z  E kin  Q dus mgh  21 mw 2  Fw s 
mgh  21 mv 2  Fw s  100x 10x 8  0,5x 100x 10,82  Fw x 10 
8000  5832  10Fw  Fw  2.168 / 10  217(N )
C Remmen betekent dat er warmte ontstaat uit de kinetische energie
E kin  Q dus
1
2
mv 2  Frem s 
0,5x 100x 10,82  Frem x 6,55 
5.832  6,55Frem  Frem  5.832 / 6,55  890(N )
V
FLIPPEREN
A
Eerst veersterkte c uit rek u en benodigde kracht F:
c
B
F 40( N ) 40( N )


 2000( N / m)
u 2(cm) 0,02(m)
Bij lanceren wordt veerenergie omgezet in kinetische energie
Eveer  Ekin dus
1
2
cu 2  12 mv 2 
1
0,05v 2  0,4  0,025v 2 
2
v 2  0,4 / 0,025  16  v  16  4,0(m / s)
1
2
2000.0,02 2 
C
De kast staat schuin, er ontstaat dus zwaarte energie uit kinetische energie
Ekin  E z  Ekin ' dus
1
2
mv 2  mgh  12 mw2 
w2  v 2  2 gh  4 2  2 x10 x0,10  14 
w  14  3,7(m / s)
VI
A
WINDMOLEN
De cilinder lucht die de wieken per seconde
passeert heeft als volume
V / t  v. A  7(m / s) x10(m2 )  70(m3 / s)
en dus als massa
m / t  .V / t  1,3(kg / m3 ) x70(m3 / s)  91(kg / s)
B
Het in- en uitkomende vermogen volgend uit de kinetische energie
in de lucht
m
Pin 
1
2
vin2  0,5 x91x7 2  2230( J / s )
t
m 2
Puit  12 vuit
 0,5 x91x32  410( J / s)
t
C
Rendement is nuttig deel, dus:

Pnuttig
Pin
Pin  Puit 2230  410


 0,82 
Pin
2230
Het rendement is maximaal 82%
4 SJOELEN
Co BTn
SJOELEN
Energiebehoud:
Lanceren
Remmen
Botsen
Evoor = Ena
Eveer  Ekin
Ekin -> Q
Ekin,wit  Ekin,wit’’ + Ekin,zwart’’
A
veersterkte
Trekken met de Newtonmeter
levert de benodigde kracht F
bij een rek u: de sterkte c 
F = 0,66 (N)
u = 4 cm
F
0,66(N )
c 

 16,5(N / m )
u
0,04(m )
F
u
u
F
c
cgem
(cm)
(N)
(N/m)
(N/m)
1
0,13
13,0
2
0,32
16,0
3
0,50
17,7
4
0,66
16,5
5
0,85
17,0
17
B
Wrijvingskracht meten
Remweg Δs meten bij verschillende rek u om Fw te berekenen
u
Δs
Directe meting met treintje van 10 sjoelschijven
Proef B
Wrijving berekenen
Je kunt de wrijving op de tafel Fw op twee manieren bepalen:
(1) berekenen uit de remweg Δs via Eveer  Q,
dus
1
2
cu 2  Fw s
(2) meten met een Newtonmeter (treintje van 10 schijven)
Veerenergie:
Eveer  21 cu 2  0,5x 17x 0,012  0,00085(J )
Wrijving:
Eveer  Fw s  Fw 
u
Eveee
0,00085

 0.043(N )
s
0,02
Δs
Eveer
Fw
Fgem
(cm)
(cm)
(J)
(N)
(N)
1
2
0,00085
0,043
2
8
0,00340
0,043
3
19
0,00765
0,040
4
33
0,01360
0,041
5
52
0,02125
0,041
0,042
C Botsing in een plaatje
Δs2 = 36 cm
u = 5 cm
Δs1 = 24 cm
Δs3 = 20 cm
C Botsing: berekening snelheden
Snelheid witte schijf na de botsing uit remweg van 36 cm
1
2
E kin  Q dus
uwit 
2
mu wit
 Fw s 
2Fw s

m
2x 0, 042x 0,36

0,02
uwit  1,23 (m / s )
Snelheid zwarte schijf na de botsing uit remweg van 20 cm
E kin  Q dus
u zwart 
1
2
2
mu zwatt
 Fw s 
2Fw s

m
2x 0,042x 0,20

0,02
u zwart  0,92 (m / s )
Snelheid witte schijf voor de botsing uit rek van 7 cm en remweg van
24 cm:
2
Eveer  E kin  Q dus 21 cu 2  Fw s  21 mv wit

2
0,5x 17 x 0,052  0,042x 0,24  0,5x 0,020xv wit

2
0,02125  0,00100  0,010v wit

v wit  0,02025
0,0100
 1,43(m / s )
C botsing: controle E-behoud
uwit=1,23
We kijken bij de botsing of er
wel energiebehoud geldt!
Kinetische energie voor de botsing:
2
Evoor  Ekin  21 mv wit
 0,5x 0,020x 1,422  0,02026(J )
Kinetische energie na de botsing:
1
1
2
2
mu wit
 mu zwart
2
2
2
2
 0,5x 0,020x (1,23  0,98 )  0,02473( j )
E na  E kin ,wit  E kin , zwart 
E na
Meetfout:
0,02473  0,02026  0,00447(J )
In procenten:
fout 
verschil
0,00447
x 100 
x 100  18%
goed
0,02473
vwit=1,42
uzwart=0,98
EXTRA
I
AUTORIJDEN
A Eerst de resulterende kracht dan de wrijving:
R  ma  100 x0,5  500(N)

R  Fm -Fw  500  2000-Fw  Fw  1500(N)
B Natuurkunde is vaak tegen intuïtief. Rutger heeft gelijk , let op de
redenering: snelheid constant

versnelling 0 
resulterende kracht 0

Fm=Fw
C Vermogen uit snelheid en kracht:
W
F .s
s
P 

 F .  F .v
t
t
t
D Invullen van deze formule levert het mechanisch vermogen,
P  Fw xv  1500( N ) x 25(m / s)  37500( J / s)  3,75 x10 4 (W )
Energie haal je uit vermogen en tijd,
E  Pt  37,5x 10 3 (W )x 5x 3600(s )  6,75x 10 8 (J ))
E Rendement Ech  Emech + Q is 30%, dus:
E mech
6,75x 10 8
E ch 

 2,25x 10 9 (J )
0,3
0,3
Er is hier heel wat liter benzine voor nodig (32 (MJ/li)):
E. ch
2250(MJ )
V 

 70(li )
Everbr
32(MJ / li )
II
SJOELEN
A Veersterkte
c 
F
3,5(N )

 50(N / m )
u
0,07(m )
B Voor het lanceren geldt de omzetting EveerEkin, dus
1
2
cu 2  21 mv 2
dus
50x(0,05) 2  0,020v 2 
v 2  502x0,052 
v  50x0,5  2,5(m/s)
C Tijdens het remmen is de omzetting EkinQ, dus
1
2
mv 2  F w s dus
1
2
0,02x2,5 2  Fw 0,73 
Fw 
0,0625
 0,086(N )
0,73
.
D De meetfout is
verschil
0,091  0,086
x 100 
x 100  5,5%
goed
0,091
E Dit komt doordat:
(1) de tafel niet overal even glad zal zijn,
(2) de c wellicht niet constant is en
(3) leerlingen de boel weer eens verzieken!
III
WITTE STEENKOOL
A De omzetting is hier Ez Qwater + Erest.
Vanwege het rendement van 15% kun je uit
de valhoogte de temperatuurstijging halen,
85% gaat zitten in warmte:
Q  0,85 xEz  0,85mgh  mcT 
0,85 gh 0,85 x10 x400
T 

 0,8( o C )
c
4200
B Die 15% restenergie wordt gebruikt om de lampen te laten branden:
E rest  Pt  0,15mgh  P  0,15
m
gh  0,15x 100x 10 3 x 10x 400  6,0x 10 7 (W )
t
Uit dit grote vermogen kunnen heel wat 100 W lampen branden, nl. 6x105!
IV
HELLEND VLAK
A Boven is er zwaarte-energie,
Ez = mgh
Ez = 0,2x10x0,8 = 1,6(J).
B Met wrijving omlaag glijden heeft als
omzetting
Ez  Ekin + Q.
C De schuine zijde AB is 1,6 m, want
sin30 =ov/sch=0,8/AB.
Uit mgh=½mv2+FwΔs volgt
1,6=0,5x0,2xv2+0,5x1,6.
Rekenen:
1,6=0,1v2+0,8  v=√(0,8/0,1) = 2,(m/s)..
D Op BC is de omzetting Ekin Q, dus
½mv2=FwΔs
 0,5x0,2x4 = 0,7Δs
 Δs = 0,4/0,7 = 0,58(m)
V
PERPETUUM MOBILE
A Ken je nog de Bram uit 1976? Het smalle buisje dat door
de capillaire werking water opzuigt? Het water gaat omhoog,
volgt de bocht en laat even later de druppel op turbines vallen.
Vallen? De druppel valt door capillaire werking juist NIET!
Een PM is een plaatje van een apparaat dat het LIJKT te doen.
B Formulering (1): Er bestaat geen machine die zonder brandstof werkt.
Formulering (2): Energie kan niet zo maar ontstaan (of verdwijnen).
Formulering (3): Bij elk proces geldt Evoor=Ena.
C Afleiding
(zie sheet 35)
Ekin W  F .s  m .a .s  m . v .s 
 t 
Ekin  m .v . s   m .v .vgem  m .v . 21v  21 mv
 t 
2
D Eenhedencontrole
E kin   21 mv 2   m v 2  kg.m 2 / s 2  kg.m / s 2 .m  Nm  J
EINDE