uitwerkingen opgaven les 19

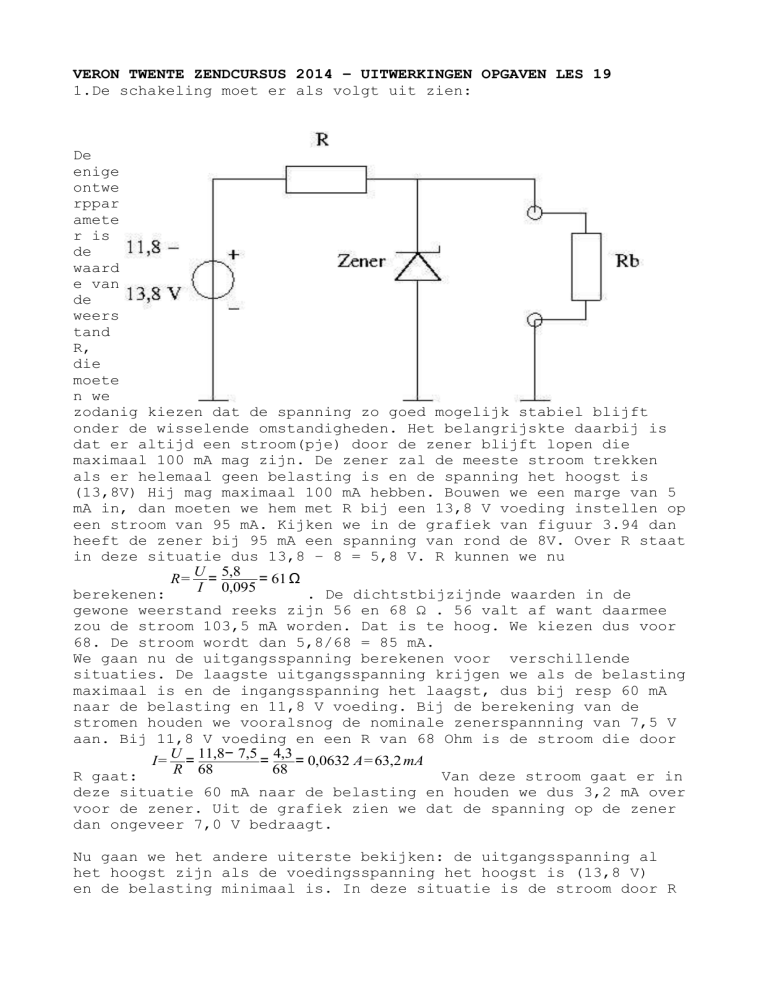
VERON TWENTE ZENDCURSUS 2014 – UITWERKINGEN OPGAVEN LES 19
1.De schakeling moet er als volgt uit zien:
De
enige
ontwe
rppar
amete
r is
de
waard
e van
de
weers
tand
R,
die
moete
n we
zodanig kiezen dat de spanning zo goed mogelijk stabiel blijft
onder de wisselende omstandigheden. Het belangrijskte daarbij is
dat er altijd een stroom(pje) door de zener blijft lopen die
maximaal 100 mA mag zijn. De zener zal de meeste stroom trekken
als er helemaal geen belasting is en de spanning het hoogst is
(13,8V) Hij mag maximaal 100 mA hebben. Bouwen we een marge van 5
mA in, dan moeten we hem met R bij een 13,8 V voeding instellen op
een stroom van 95 mA. Kijken we in de grafiek van figuur 3.94 dan
heeft de zener bij 95 mA een spanning van rond de 8V. Over R staat
in deze situatie dus 13,8 – 8 = 5,8 V. R kunnen we nu
U 5,8
R= =
= 61 Ω
I 0,095
berekenen:
. De dichtstbijzijnde waarden in de
gewone weerstand reeks zijn 56 en 68 Ω . 56 valt af want daarmee
zou de stroom 103,5 mA worden. Dat is te hoog. We kiezen dus voor
68. De stroom wordt dan 5,8/68 = 85 mA.
We gaan nu de uitgangsspanning berekenen voor verschillende
situaties. De laagste uitgangsspanning krijgen we als de belasting
maximaal is en de ingangsspanning het laagst, dus bij resp 60 mA
naar de belasting en 11,8 V voeding. Bij de berekening van de
stromen houden we vooralsnog de nominale zenerspannning van 7,5 V
aan. Bij 11,8 V voeding en een R van 68 Ohm is de stroom die door
U 11,8− 7,5 4,3
I= =
=
= 0,0632 A=63,2 mA
R 68
68
R gaat:
Van deze stroom gaat er in
deze situatie 60 mA naar de belasting en houden we dus 3,2 mA over
voor de zener. Uit de grafiek zien we dat de spanning op de zener
dan ongeveer 7,0 V bedraagt.
Nu gaan we het andere uiterste bekijken: de uitgangsspanning al
het hoogst zijn als de voedingsspanning het hoogst is (13,8 V)
en de belasting minimaal is. In deze situatie is de stroom door R
U 13,8− 7,5 6,3
=
=
= 0,0926 A= 92,6 mA
R 68
68
.Daarvan gaat er 40 mA naar de
belasting, dus voor de zener blijft dan over 92,6 -40 = 52,6 mA.
In de grafiek lezen we nu de spanning van de zener af bij deze
stroom en vinden rond de 7,5 V. Onder de gevraagde condities
varieert de uitgangsspanning dus tussen de 7,0 en 7,5 V.
I=
2.De schakeling moet er a.v. uit zien:
Het ontwerp betreft nu naast de keuze van de waarde van R ook de
keuze van de zener. In figuur 2.54 staan een aantal zeners.
De uigangsspannning naar de belasting is in dit schema de zener
spanning minus de drempelspanning van de basis/emitter diode van
de 2N3055. We moeten ontwerpen op een spanning rond de 5,8 V
De zener moet dan de spanning stabiliseren rond de 5,8 + 0,7=
6,5V. De geschikte zener uit het rijtje is dan de 6V2.
Voor de verdere redenering is het goed te weten wat de invloed van
de 3 gegevens parameters (a) ingangsspanning, (b) belasting en c)
de stroomversterkingsfactor β op de uitgangsspanning is:
a) hogere ingangsspanning betekent meer stroom door R en dus
een hogere stroom door de zener. In de grafiek zie je dan dat
ook de spanning over de zener toeneemt en daarmee krijgen we
dus ook een hogere uitgangsspanning (die is 0,7 V lager dan
de zenerspanning.
b) grotere belasting betekent een grotere basisstroom door de
transistor ( Ibasis = Ibelasting/β). Dat betekent dat er
minder stroom overblijft voor de zener en dat (zie grafiek)
geeft een lagere zenerspanning en dus ook een lagere
uitgangsspanning
c)
een grotere β betekent dat de basisstroom die nodig is om
de belastingsstroom te leveren kleiner wordt. Er blijft dus
meer stroom over van de stroom die door R wordt aangevoerd om
door de zener te gaan. Meer zenerstroom (zie grafiek) geeft
een hogere zenerspanning en dus ook een hogere
uitgangsspanning
In tegenstelling tot de methode in de les getoond, laat ik hier nu
zien hoe je te werk kunt gaan bij een ontwerp op de gemiddelden
van de drie parameters. We rekenen nu de waarde van R uit op het
gemiddelde van de drie gegeven parameters, dus voor een
ingangsspanning van 18 V, een belasting van 1,25 Ampere en een β
van 60 .
In deze situatie is stelt de basisstroom zich in op 1,25/60 =
0,0208 A = 20,8 mA. We willen de zener nu instellen op een stroom
van 100mA ( is de helft van de toegestane waarde) De totale stroom
door de weerstand R is dan 100 + 20,8 = 120,8 mA. De spanning over
de weerstand is de ingangsspaning minus de zenerspanning dus
18 – 6,5 = 11,5 V. Dus R moet dan worden U/I = 11,5/0,1208=95 Ohm.
De dichtstbijzijnde praktijkwaarde van de weerstand is dan 100
Ohm. Met die waarde gaan we bij de verschillende combinaties van
ingangsspanning en uitgangsstroom de uitgangspanning bereken.
Hoogste uitgangsspanning krijgen we dus (zie boven) bij de hoogste
voedingsspanning (= 20 V), de laagste uitgangsstroom (= 0,5 A) en
de hoogste β (100). Die situatie gaan we nu doorrekenen.
De belasting trekt 0,5 A = 500 mA. Met een β van 100 trekt de
basis dus 500/100 = 5 mA. De totale stroom door de 100 Ohm
20− 6,5
I R=
= 0,135 A=135 mA
100
serieweerstand is
. Daarvan gaan er 5 naar
de basis van de tor (500/100=5) en er blijven dus 135-5 = 130 mA
over voor de zener. De lijn in de grafiek komt niet zover maar
geschat is de spanning van de zener daar zo'n 7 V. De
uitgangsspanning is dan 7 – 0,7 = 6,3 V.
Nu berekenen we de toestand in het andere uiterste:
voedingsspanning = + 16V, belasting is 2 A en de β= 20. dan
krijgen we dat de stroom door de basis van de transistor gelijk
2
I B=
= 0,1 A=100 mA
20
wordt aan:
. De stroom door de weerstand is
I R=
16− 6,5
= 0,095 A=95 mA
100
. Die stroom is minder dan de basis afneemt.
Dus voor de zener blijft niets over. Dat betekent dat spanning op
de basis van de 2N3055 daalt. Deze spanning is te berekenen met de
wet van Ohm over de serieweerstand:
U R =I∗ R= 0,1∗ 100= 10 V .
De spanning op het knooppunt met de basis wordt
dus 16 – 10 = 6V. De uitgangsspanning is in feite niet meer
gestabiliseerd en wordt 6 – 0,7 = 5,3 V. Om deze schakeling goed
te kunnen laten werken zou de tor minder dan 95 mA basisstroom
moeten trekken in deze situatie. Dat betekent dat zijn β minimaal
2/0,095 = 21 zou moeten zijn. Als dat het geval is
begint de zener net te werken en krijgt de basis een spanning die
volgens de grafiek 6,2 V is. De uitgangsspanning is dan 6,2 – 0,7
= 5,5 V.
3.De spanningsversterking van deze schakeling is volgens de
Rc 6,8
=
= 6,8
Re 1
formule
en daarmee onafhankelijk van de hfe. Antwoord is
dus d
4. De schakeling is een parallelschakeling van twee seriekringen
die zijn afgestemd op dezelfde resonantie frequentie
1
f res =
2∗ Π∗ √
L∗ C . Het product L*C is voor beide kringen gelijk
want links is de capaciteit 2 * zo klein als rechts maar de
spoel links is 2 * zo groot als rechts. Bij de
resonantiefrequentie is de impedantie van een serie L/C kring
zonder weerstand nul. We krijgen bij de resonantiefrequentie
dus te maken met een parallel schakeling van twee zuivere
weerstanden van 100 Ohm ; antwoord dus 50 Ohm = d.
5. Bij resonantie heeft de parallelkring van L en C een oneindig
hoge weerstand dus hoge Q en een smalle hoge resonantiepiek.
Bij het sluiten van de schakelaar wordt de kring belast met
de weerstand R. De spanning over de kring wordt de helft
(spanningsdeler van R en R) kleiner. De kring zelf wordt
belast met een weerstand R en krijgt dus een lagere Q waarmee
de resoantiepiek breder wordt. Antwoord dus c.
8. Het filter heeft de vorm van een T, niet van een Pi. Het heeft
in de langstak twee spoelen, dus laat geen hoog door. Het is ook
geen bandsperfilter want het sluit niet een bepaalde frequentie
naar aarde kort. Antwoord dus b
9. Door de horizontale weerstand wordt de condensator als de puls
hoog gaat opgeladen. De laadkromme van een condensator is bol. Dat
is als volgt in te zien: als je start met een lege condensator
gaat er een stroom lopen die de spanning op de condensator doet
toenemen. De laadstroom door een R wordt steeds kleiner omdat het
spanningsverschil over de weerstand steeds kleiner wordt. De
spanning op de condensator stijgt dus in het begin sneller dan
later als de condensator steeds meer spanning krijgt. De
laadstroom wordt nul als de condensator de spanning U1 heeft
bereikt. Gaat de puls naar nul dan ontlaadt de condensator zich
over de weerstanden. De ontlaadstroom is in het begin van de
negatieve puls het grootst omdat ook dan weer het spanningverschil
over de weerstanden het grootst is. De spanning zak dus snel in.
Later als de spanning vand e condensator als is gezakt gaat het
ontladen steeds langzamer en zakt de spanning dus minder snel. De
ontlaadkromme is dus hol. Antwoord tekening 4 = c