EngWH11

Gemeenschappelijke Propedeuse Engineering
H. 11
WISKUNDE
H.11
Differentiaalrekening
Een van de meest toegepaste onderwerpen in de wiskunde is de
differentiaalrekening en in het verlengde hiervan de integraalrekening.
In deze cursus beperken we ons tot de differentiaalrekening.
Toepassingen hiervan vinden we o.a. in de natuurkunde, bijvoorbeeld bij het
berekenen van de snelheid of versnelling van een voorwerp, in de elektriciteitsleer bij
het beschrijven van stroom- of spanningsverloop in elektrische schakelingen of
‘gewoon’ bij het onderzoek van het verloop van functies (grafisch).
11.1
Raaklijn en afgeleide
Grafieken van veel functies hebben in het algemeen een ‘glad’ verloop.
Als voorbeeld kijken we naar de grafiek van de functie:
f ( x)  x 2  3 x  4
We nemen een willekeurig vast punt op deze grafiek, A(2 , 2) , en een verderop
gelegen punt B.
Voor dit punt B nemen we eerst het punt B(4 , 8) en kijken naar de richting van het
lijnstuk (de ‘koorde’) AB:
x groeit van x1 = 2 naar x2 = 4 ; dit noteren we als x = 2.
Als x groeit van x1 = 2 naar x2 = 4, dan groeit y van y1 = 2 naar y2 = 8.
Dit noteren we als y = f(x) = 8 - 2 = 6.
y
De relatieve verandering van y ten gevolge van de verandering in x is
en dit
x
noemen we het differentiequotiënt van de functie f(x) , hier dus
y 6
 3
x 2
Het differentiequotiënt geeft de richtingscoëfficiënt (rico) aan van het lijnstuk AB
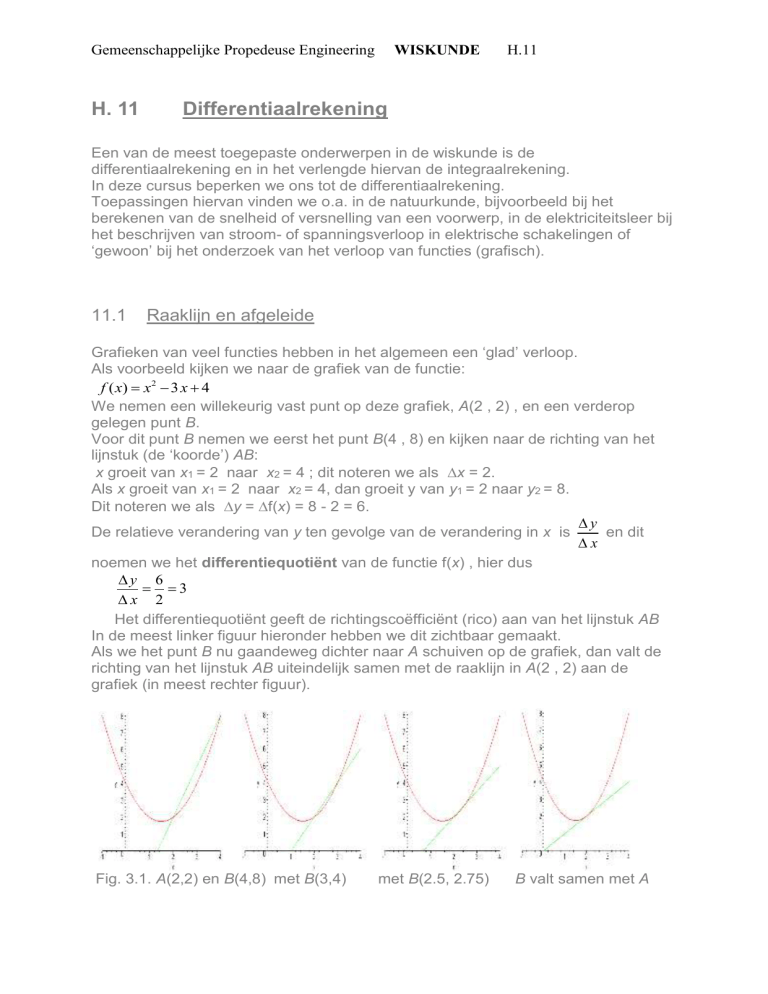
In de meest linker figuur hieronder hebben we dit zichtbaar gemaakt.
Als we het punt B nu gaandeweg dichter naar A schuiven op de grafiek, dan valt de
richting van het lijnstuk AB uiteindelijk samen met de raaklijn in A(2 , 2) aan de
grafiek (in meest rechter figuur).
Fig. 3.1. A(2,2) en B(4,8) met B(3,4)
met B(2.5, 2.75)
B valt samen met A
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.11
Dit proces van een steeds kleinere aangroeiing van x nemen (B steeds dichter bij A)
is in onderstaande tabel nog wat gedetailleerder zichtbaar gemaakt.
X1
X2
x
y
2
2
2
2
2
2
2
4
3
2.5
2.2
2.1
2.01
2.001
2
1
0.5
0.2
0.1
0.01
0.001
6
2
0.75
0.24
0.11
0.0101
0.001001
y
x
3
2
1.5
1.2
1.1
1.01
1.001
Als de aangroeiing x erg klein wordt, ofwel tot nul nadert,
y
y
1
dan nadert het differentiequotiënt
tot 1.
Notatie:
x
x
Op het moment dat
Notatie:
y
y
dy
precies 1 wordt noteren we dit i.p.v.
als
.
dx
x
x
dy
1
dx

y 
 1
Opmerking : de formele notatie is : lim
x 0  x


dy
We noemen
het differentiaalquotiënt van de functie f(x) in het punt A(2 , f(2)).
dx
De meetkundige betekenis hiervan is, dat het differentiaalquotiënt de richting
aangeeft van de raaklijn in het punt A(2 , f(2)) aan de kromme.(zie fig. 3.1.)
Het berekenen van het differentiaalquotiënt op deze manier voor steeds andere
punten A op de grafiek van f(x) zou erg omslachtig zijn.
Daarom gebruiken we een aantal regels om het differentiaalquotiënt van een functie
f(x) te bepalen.
We noemen dit proces differentiëren of de afgeleide functie bepalen.
Andere namen voor de afgeleide functie zijn:
de afgeleide
de eerste afgeleide
het differentiaalquotiënt
Voor de afgeleide functie gebruiken we de volgende symbolen:
-
f '( x)
-
y'
df
dx
of
of
dy
dx
 gebruiken we als de functie is gegeven als: f  x  
 gebruiken we als de functie is gegeven als: y 
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.11
In § 11.2 worden differentieerregels en standaardafgeleiden gegeven, waarmee we
van een gegeven functie de afgeleide functie kunnen bepalen.
De afgeleide van de eerder in de inleiding gebruikte functie
f ( x)  x 2  3 x  4 wordt dan:
f '( x)  2 x  3
Als we deze afgeleide bepalen voor x = 2 dan krijgen we:
f '(2)  2  2  3  1
Dit resultaat hadden we eerder via de tabel al bepaald!
11.2 Standaardafgeleiden en differentieerregels
Als we een functie f (x) differentiëren dan krijgen we de afgeleide functie f '( x) .
Het bepalen van de afgeleide functie doen we m.b.v. een aantal standaardafgeleiden
en differentieerregels (de onderstaande lijsten zijn niet volledig).
Standaardafgeleiden:
S1.
f ( x)  c 
f '( x)  0
S2.
f ( x)  x n
S3.
f  x 
S4.
f ( x)  sin  x  
f '( x)  cos  x 
S5.
f ( x)  cos  x  
f '( x)   sin  x 
S6.
f ( x) 

x 
ex

(c is een constante)
f '( x)  n  x n  1
f ' x 
f '( x) 
(voor elke n)
1
2 x
ex
Differentieerregels:
D1.
y  c  f ( x) 
D2.
y  f ( x)  g ( x) 
D3.
y  f ( x)  g ( x) 
D4.
y
f ( x)
g ( x)

y '  c  f '( x)
y' 
(c is een constante)
y '  f '( x)  g '( x)
y '  f '( x)  g ( x)  f ( x)  g '( x)
f '( x)  g ( x)  f ( x)  g '( x)
 g ( x) 
2
Somregel
Productregel
Quotiëntregel
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.11
Voorbeelden:
1a.
f ( x)  8 
f '( x)  0
1b.
f ( x)  38 
2a.
f  x   x4
2b.
f t   2 t 3 
3a.
f  x 
3b.
y
4a.
y  x 4  x 2  10 
4b.
f ( x)  4 x 3  5 x  8 
5a.
f ( x)  2  sin  x  
5b.
f ( x)  3cos  x   2 x  2 x
6a.
y  x 2  sin  x  
6b.
f ( x)  4 x  cos  x  
df
 2  cos  x   4 x  sin  x 
dx
7a.
f ( x) 
2x

x 1
2  ( x  1)  2 x 1
2

2
( x  1)
( x  1) 2
7b.
f ( x) 
4x

2 x 1
8a.
f ( x) 
8b.
f ( x) 
9a.
f ( x)  x  e x 
9b.
f (t ) 
f '( x)  0
df
 4 x3
dx

df
 6t2
dt
1
 x 2
x2
2
 2 x 3 
x3
sin  x 
f '( x)  2 x  3 

dy
6
 6 x 4  4
dx
x
y '  4 x3  2 x
df
 12 x 2  5
dx
f '( x)  0  cos  x   cos  x 

f '( x) 
f '( x) 
4  (2 x  1)  4 x  2
4

2
(2 x  1)
(2 x  1) 2
f '( x) 
x2

cos  x 
f '( x) 
et
t

df
1
 3sin( x)  2 
dx
x
dy
 2 x  sin  x   x 2  cos  x 
dx

x
2
x3
x cos  x   sin  x  1
x
2

x  cos  x   sin  x 
cos  x   2 x  x 2 sin  x  2 x  cos  x   x 2 sin  x 

cos( x) 2
cos( x) 2
f '( x)  1 e x  x  e x  e x  1  x 
f '(t ) 
x2
x
t  e x  1 e x e  t  1

t2
t2