Tentamen Optica 3BOX1 – 30 jnuari 2014 – antwoorden

Tentamen Optica 3BOX1 – 30 jnuari 2014 – antwoorden
Opgave 1: Breking en reflectie
x 
d  d ' tan θi sin θi nlucht 1
≈
=
=
a.
⇒ =
x
d tan θt sin θt
n
n
tan θt =
d ' 
tan θi =
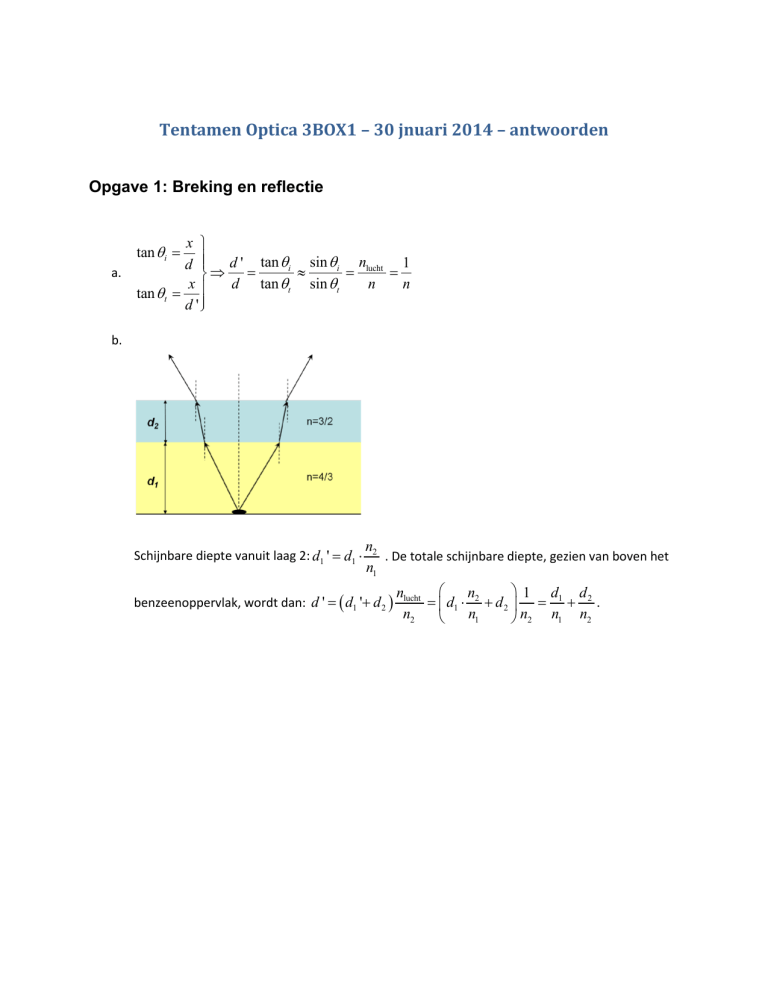
b.
Schijnbare diepte vanuit laag 2: d1=' d1 ⋅
n2
. De totale schijnbare diepte, gezien van boven het
n1
benzeenoppervlak, wordt dan: d ' = ( d1 '+ d 2 )
1 d d
nlucht 
n
=  d1 ⋅ 2 + d 2  = 1 + 2 .
n2
n1

 n2 n1 n2
Opgave 2: polarisatie
 cos 2 α
a. 
 sin α cos α
sin α cos α   1 
 cos α 
=
cos
α




 . Deze Jones vector komt overeen met projectie
sin 2 α   0 
 sin α 
van het elektrische veld in de x-richting op de doorlaatrichting van de polarisator:
 cos 2 α

 sin α cos α
sin α cos α   0 
 cos α 
   = sin α 
 . Deze Jones vector komt overeen met projectie
2
sin α   1 
 sin α 
van het elektrische veld in de y-richting op de doorlaatrichting van de polarisator:
b. Na de eerste polarisator I1 = I 0 / 2 .
 1/ 4
Na de tweede polarisator: 
 3/4

 12 
3 / 4  1/ 2 −i / 2   1  1  1 + i 3  1
1+ i 3 
=



 =

 1 3 
3 / 4   i / 2 1/ 2   0  8  3 + 3i  4
2


dus lineair gepolariseerd onder een hoek van 60 met de x-as (zoals te verwachten).
Uit dit resultaat volgt voor de irradiantie na de tweede polarisator:
2
 12 
I
I
1
I2 =
I1 ⋅ 1 − i 3 
=1 =0 .

 1 3
4
4 8
2

(
)
(
)
Er staat echter een fout in de opgave: de Jones matrix van het kwart lambda-plaatje moet zijn:
I1 I 0
1 1 −i 
=
. Dit kun je ook snel inzien als je je realiseert dat het kwart-lambda
2

 , zodat I=
2 4
2 i 1 
plaatje met de snelle as onder een hoek van 45 met de x-as het lineair gepolariseerde licht na de
eerste polarisator circulair maakt, zonder verlies van irradiantie. Dit circulair gepolariseerde licht kan
ontbonden worden in een component evenwijdig aan de doorlaatrichting van de tweede polarisator
en een component daar loodrecht op zodat de helft van de irradiantie I1 door de tweede polarisator
wordt doorgelaten (dit geldt voor iedere hoek α ).
c. Om alle licht dat door polarisator 1 komt ook door polarisator 2 te krijgen, moet de lineaire
polarisatie in de x-richting omgezet worden in lineaire polarisatie met een hoek van 60 met de x-as.
Dit kun je voor elkaar krijgen met een half-lambda plaatje met de snelle (of de trage) onder een hoek
van 30 met de x-as, aangezien de polarisatie gespiegeld wordt t.o.v. de snelle (trage) as. Twee
kwart-lambda plaatjes na elkaar, ieder met de snelle (of de trage) as onder een hoek van 30 met de
x-as, geven hetzelfde effect. Dat is dus de gevraagde configuratie. Bij maximale transmissie komt
alles door de tweede polarisator heen, dus I 2,max =
I0
.
2
Opgave 3: Dikke lens
a. Ieder grensvlak heeft een brandpunt aan de voorwerpzijde ( f o =
beeldpuntzijde ( f i =
na
R ) en aan de
nb − na
nb
R ).
nb − na
en
Voor het lucht-glas grensvlak
3/ 2
fi1 =
(−2 R) =
−6 R ⇒ z ( Fi1 ) =
−6 R .
3 / 2 −1
Voor het glas-lucht grensvlak
en
.
b. Afbeelding door het lucht-glas grensvlak:
Afbeelding door het glas-lucht grensvlak:
c. Gebruik
na nb nb − na
n s
en M T = − a i .
+ =
so si
R
nb so
met vergroting
Lucht-glas grensvlak:
Glas-lucht grensvlak: s02 = R − si1 =4 R ⇒ si 2 =8 R ⇒ zi 2 =9 R met vergroting
Totale vergroting
.
Opgave 4: Michelson interferometer
a. Laat optische weglengtes door glas buiten beschouwing (zijn gelijk voor beide armen). De bundel
2π
in arm 1 doorloopt dan een faseverschil: λ
2
2π
λ
( L2 − d vac ) + 2n
2π
λ
2L1
. In arm 2 doorloopt de bundel een faseverschil
d vac + π
t.g.v., respectievelijk, de optische weglengte door vacuüm, de
optische weglengte door het gas in de vacuümkamer en de extra fasesprong π t.o.v. arm 1 t.g.v.
de externe reflectie aan de beam splitter. Het faseverschil tussen de 2 samengevoegde bundels
bedraagt dus
δ=
4π
λ
( L2 − L1 ) +
4π
λ
(n − 1)d vac + π =
4π
λ
d+
4π
λ
(n − 1)d vac + π
. De complexe
iδ
=
E ( E0 / 2)(1 + e ) , en de irradiantie op
amplitude van de samengevoegde bundels wordt dan
=
I
scherm S:
E2
E2
1
1
iδ
) ε 0 c 0 (1 + cos=
ε 0 c 0 (1 + eiδ )(1 + e −=
δ)
ε 0 cE0 2 cos 2 (δ / 2)
2
4
4
2
; QED.
) en lege vacuumkamer (
) volgt uit de gegeven formule dat
b. Voor gelijke armlengtes (
de irradiantie minimaal is. Vier keer van donker naar licht en van licht naar donker: