Fuzzy Logic

Fuzzy Logic
1. Fuzzy Sets
Een basisbegrip in fuzzy systemen is een zgn. Fuzzy (sub)set. Dit is vrijwel gelijk aan het wiskundige
begrip “verzameling”.
Hier volgt een voorbeeld.
Eerst bepalen we een domein van alle reele getallen tussen de 0 en 10, welke we set X noemen.
Uit deze set X halen we een subset A, met alle reele getallen tussen de 5 en 8.
A = [5, 8]
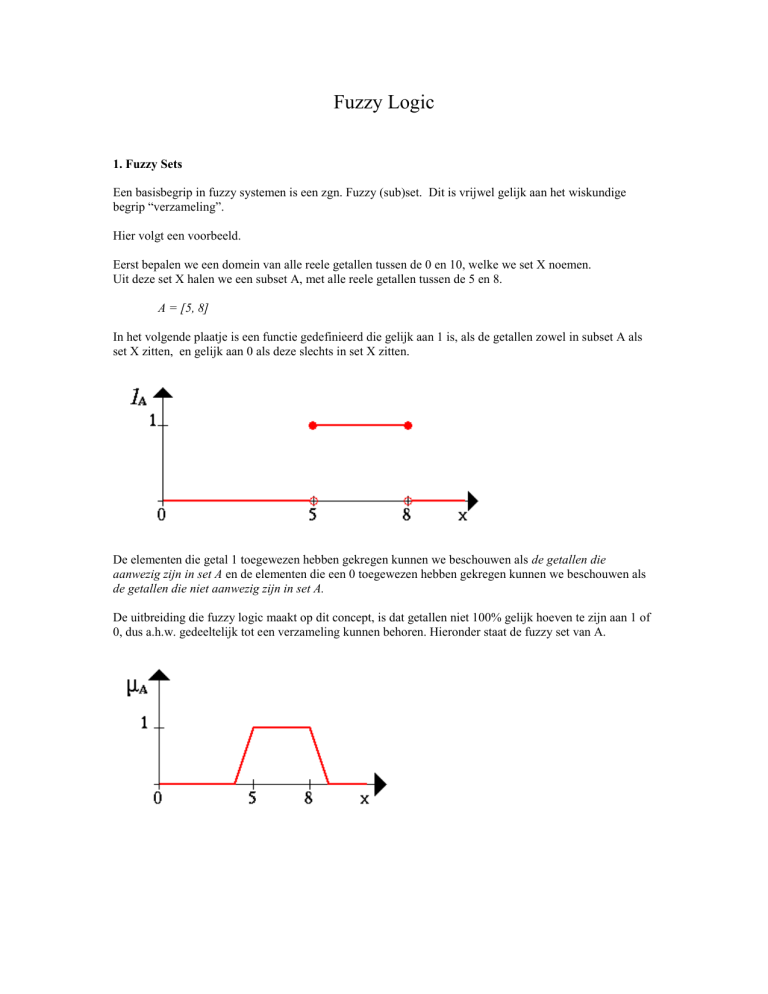
In het volgende plaatje is een functie gedefinieerd die gelijk aan 1 is, als de getallen zowel in subset A als
set X zitten, en gelijk aan 0 als deze slechts in set X zitten.
De elementen die getal 1 toegewezen hebben gekregen kunnen we beschouwen als de getallen die
aanwezig zijn in set A en de elementen die een 0 toegewezen hebben gekregen kunnen we beschouwen als
de getallen die niet aanwezig zijn in set A.
De uitbreiding die fuzzy logic maakt op dit concept, is dat getallen niet 100% gelijk hoeven te zijn aan 1 of
0, dus a.h.w. gedeeltelijk tot een verzameling kunnen behoren. Hieronder staat de fuzzy set van A.
2. Operaties op fuzzy sets
Nu we weten wat fuzzy sets zijn, kunnen we de basisoperaties hierop introduceren. Deze zijn gelijk aan de
operaties voor de verzamelingen. Deze operaties zijn dus: doorsnede, vereniging en negatie. Hieronder
worden grafische voorstellingen gemaakt van operaties op fuzzy sets.
De set A is een fuzzy interval tussen 5 en 8 en de set B is een fuzzy getal van ongeveer 4.
Het volgende figuur toont set A VERENIGD MET set B. (zie de blauwe lijn)
Het volgende figuur toont de DOORSNEDE van set A en set B. (zie de blauwe lijn)
Het volgende figuur toont een voorbeeld van NEGATIE. De blauwe lijn is negatie van set A.
3. Fuzzy regeling
Met behulp van fuzzy logic controllers zijn complexe situaties op te lossen, zonder gebruik te maken van
conventionele differentiaalvergelijkingen. Om zo’n controller te verkrijgen moet er een variabele worden
gedefinieerd die de toestand van een object omschrijft d.m.v. de waarde die het bevat. Verder moeten er
verzamelingen worden gedefinieerd die elk een toestand vertegenwoordigen d.m.v. een domein. Er wordt
een beginsituatie in de variabele gedefinieerd en bij veranderingen hiervan (door veranderingen in de
buitenwereld) wordt actie ondernomen, afhankelijk van het domein waarin de variabele zich bevindt.
Een voorbeeld:
Stel een berg voor met op de top een robotje. Het robotje kan naar links en naar rechts bewegen. De
beginsituatie is, dat het robotje op de top van de berg staat. De volgende verzamelingen kunnen worden
gedefinieerd:
 neg. high (cyaan)
 neg. low (groen)
 zero (rood)
 pos. low (blauw)
 pos. high (magenta)
Hetzelfde kunnen we doen met de hoek tussen het robotje en de berg en de hoeksnelheid van het robotje:
Regels
Met de verzamelingen van de vorige bladzijde kunnen we regels definieren om actie te ondernemen. Deze
regels zien er als volgt uit:
Als de hoek gelijk is aan 0 EN hoeksnelheid gelijk is aan 0 dan wordt de snelheid 0.
Als de hoek gelijk is aan 0 EN hoeksnelheid is pos.low, dan wordt de snelheid pos.low.
Deze regels kunnen worden samengevat in de volgende tabel:
|
angle
|
speed | NH
NL
Z
PL
PH
----------+-----------------------------v
NH
|
NH
e
NL
|
NL
Z
l
Z
| NH
NL
Z
PL
PH
o
PL
|
Z
PL
c
PH
|
PH
Waar NH betekent Negative High (krachtig naar rechts), en NL Negative Low (zwak naar rechts), etc.
De kracht van het Fuzzy Logic is, dat je een mate van een toestand kunt uitrekenen:
4. Literatuur
Deze uitleg is een extract van: “A Brief course in Fuzzy Logic and Fuzzy Control”, homepage:
http://www.flll.uni-linz.ac.at/pdw/fuzzy/