2 De Elektrische huisinstallatie

Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
Newton havo deel 1
25
2
De Elektrische huisinstallatie
2.1
Inleiding
Voorkennis
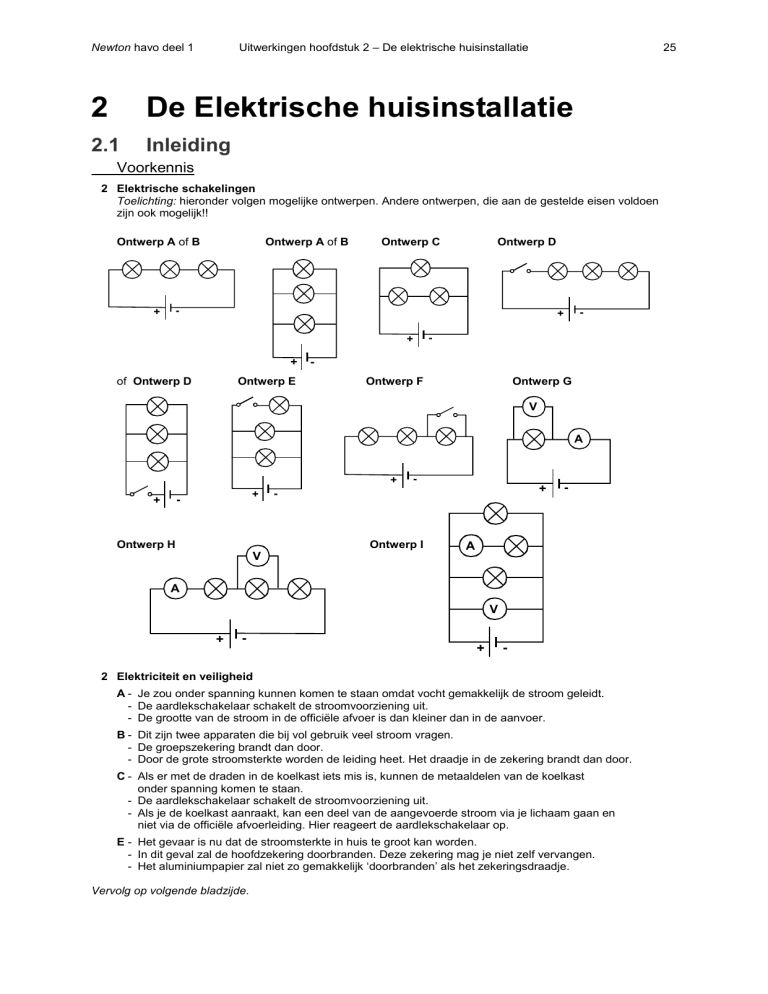
2 Elektrische schakelingen
Toelichting: hieronder volgen mogelijke ontwerpen. Andere ontwerpen, die aan de gestelde eisen voldoen
zijn ook mogelijk!!
Ontwerp A of B
+
Ontwerp A of B
Ontwerp C
Ontwerp D
-
-
+
+
+
of Ontwerp D
Ontwerp E
-
Ontwerp F
Ontwerp G
V
A
+
+
-
+
Ontwerp H
-
Ontwerp I
V
+
-
-
A
A
V
+
-
+
-
2 Elektriciteit en veiligheid
A - Je zou onder spanning kunnen komen te staan omdat vocht gemakkelijk de stroom geleidt.
- De aardlekschakelaar schakelt de stroomvoorziening uit.
- De grootte van de stroom in de officiële afvoer is dan kleiner dan in de aanvoer.
B - Dit zijn twee apparaten die bij vol gebruik veel stroom vragen.
- De groepszekering brandt dan door.
- Door de grote stroomsterkte worden de leiding heet. Het draadje in de zekering brandt dan door.
C - Als er met de draden in de koelkast iets mis is, kunnen de metaaldelen van de koelkast
onder spanning komen te staan.
- De aardlekschakelaar schakelt de stroomvoorziening uit.
- Als je de koelkast aanraakt, kan een deel van de aangevoerde stroom via je lichaam gaan en
niet via de officiële afvoerleiding. Hier reageert de aardlekschakelaar op.
E - Het gevaar is nu dat de stroomsterkte in huis te groot kan worden.
- In dit geval zal de hoofdzekering doorbranden. Deze zekering mag je niet zelf vervangen.
- Het aluminiumpapier zal niet zo gemakkelijk ‘doorbranden’ als het zekeringsdraadje.
Vervolg op volgende bladzijde.
Newton havo deel 1
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
26
Vervolg opgave 2.
F - Het dunne verlengsnoer wordt heel erg heet waardoor het plastic kan gaan smelten en
er kortsluiting ontstaat.
- De groepszekering zal doorbranden.
- Een dun verlengsnoer heeft een grotere weerstand dan een dik verlengsnoer.
De elektrische stroom zal dan een groter deel van zijn energie al in het verlengsnoer afgeven.
G - De halogeenlamp zal veel te heet worden en dus doorbranden.
- In dit geval zit de veiligheidsvoorziening meer in de lamp zelf: de gloeidraad brandt door.
- De gloeidraad die geschikt is voor 12 V krijgt nu zo’n 230 V te verduren. De stroomsterkte neemt
daardoor sterk toe met als gevolg dat er in korte tijd veel energie in de draad wordt afgegeven
waardoor deze dus te heet wordt.
2.2
Stroomkring
Kennisvragen
5 A wisselspanning ;
B gelijkspanning ;
C gelijkspanning ;
D wisselspanning ;
Oefenvragen
7 A
E gelijkspanning.
voorlamp
B
C
achterlamp
~
~
dynamo
Ad. C bij een fietsverlichting zorgen snoeren voor de ‘aanvoerleidingen’
en het metalen fietsframe voor de ‘afvoerleidingen’ van de elektrische stroom.
2.3
Spanning, stroomsterkte en weerstand
Kennisvragen
9 Er is een spanningsverschil tussen twee delen van je lichaam.
Bijvoorbeeld tussen je hand en je voeten (de grond is aarde).
Beveiliging gebeurt via een aardlekschakelaar en/of randaarde.
10 Nee, de weerstand van het menselijk lichaam zou dan kleiner dan 14  moeten zijn,
U
230
 R
 14  . Deze is echter 3 k of meer, dus de stroomsterkte I
want volgens R 
I
16
230
wordt volgens U  I  R ongeveer 230  I  1,3  103  I 
 0,077 A  77 mA .
3  103
De aardlekschakelaar schakelt de spanning uit als er een stroomsterkte van meer dan 30 mA
naar de aarde weglekt. Dus bij de gebruikte weerstandswaarde wordt de spanning uitgeschakeld.
11 De weerstand kun je bepalen door de spanning U over en
de stroomsterkte I door het apparaat te meten (zie figuur).
De weerstand R is dan te berekenen met de formule: R 
V
U
I
apparaat
- +
A
Newton havo deel 1
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
27
12 a Het verband tussen U en I is bij een constantaandraad recht evenredig en levert dus een rechte lijn op
in een U,I-diagram. Schets: zie onder b.
b Bij een gloeilamp is de weerstand niet constant, maar deze neemt toe met de temperatuur.
Als de lamp feller brandt, is de weerstand groter. Het verband tussen U en I is niet recht evenredig.
Schets a
Schets b
U
(V)
U
(V)
R groot
lamp
R klein
I (A)
I (A)
c Neem een punt op de grafieklijn in het U,I-diagram en bepaal daarvan de waarden van I en U.
U
Bereken daarna de weerstand R met behulp van de formule: R  .
I
13 a Bij 4,4 schaaldelen: U  44 V
b Bij 4,4 schaaldelen: I 
Afgerond: U = 44 V
4,4
 100  88 mA
5,0
Afgerond: I = 88 mA
U
6,0
 R
 4,0  10 2  
I
0,015
U
2,0
15 a R 
 R
 8,0 
I
0,25
Afgerond: R = 4,0102 
14 R 
Afgerond: R = 8,0 
b De stroomsterkte neemt minder snel toe in vergelijking met de spanning: de weerstand is groter.
16
U = I  R = 10,710-3  140 = 1,498 V (3 cijfers significant !)
17 U  I  R  230  I  1,3  10 3  I 
230
1,3  10 3
Afgerond: U = 1,50 V
 0,177 A
Afgerond: I = 0,18 A
U
U
respectievelijk R  .
I
R
Deze stap maak je nadat je eerst de formule U = I  R uit BINAS hebt overgenomen. Na het omwerken
kun je dan de gegevens invullen die je natuurlijk wel eerst in de afgesproken eenheden hebt genoteerd.
Vervolgens voer je de berekening uit en geef je het eindantwoord met het juiste aantal significante cijfers.
18 De formule U = I  R moet eerst omgewerkt worden in I 
Oefenopgaven
23 Lichaamsweerstand
a Met droge handen niet: U  I  R  230  I  30  10 3  I 
3
Met natte handen wel: U  I  R  230  I  3,0  10  I 
230
30  10
230
3
3,0  103
 7,7  10 3 A . Dit is kleiner dan 30 mA.
 77  103 A . Dit is meer dan 30 mA.
b Meer dan 30 mA en langer dan 0,2 s wordt gevaarlijk.
c Alle apparaten bezitten randaarde of zijn dubbel geïsoleerd. Er zijn geen open stopcontacten toegestaan.
Het metalen bad is geaard. Onder de tegelvloer behoort een metalen plaat te zijn aangebracht
die geaard is.
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
Newton havo deel 1
24 Aarding
a Bespreek de tekeningen in de klas.
Voorbeelden van tekeningen zijn:
tekening A
tekening B
I
I
I
spanningsdraad
spanningsdraad
I
waterleiding
goed
geaarde
waterleiding
I
I
I
I
I
geaarde vloer
geaarde vloer
b Bij een goede aarding zou de stroom via de waterleidingbuis naar de aarde gelopen zijn en
was het ongeluk niet gebeurd.
c Plastic is een isolator en geleidt de stroom niet de aarde in.
d In het algemeen wel, omdat hierbij wordt nagegaan of de aangevoerde stroomsterkte even groot is
als de afgevoerde stroomsterkte. Met water erbij (douche) kan de situatie wel gevaarlijk zijn.
25 Defibrillator
a Hoe kleiner de weerstand, des te groter de stroomsterkte. De weerstand en stroomsterkte zijn
niet omgekeerd evenredig, dan zouden de toppen zich namelijk moeten verhouden als 1 : 2 : 4.
Volgens de formule U  I  R betekent dit dat de gebruikte spanning U blijkbaar niet steeds hetzelfde is.
b I = 0,63  Imax = 0,63  34 = 21 A. In het diagram kun je bij lijn A aflezen dat de stroomsterkte
van ongeveer 0,2 ms tot 4,3 ms groter is dan 21 A. De tijdsduur t = 4,1 ms.
c Vocht geleidt de stroom beter, de huidweerstand neemt door gebruik van de gel af.
d Bij een huidweerstand van 50  bedraagt de piekstroom 54 A. 63% van 54 A is 34 A.
De tijdsduur van de stroompuls is dan 2,9 - 0,3 = 2,6 ms, want de stroomsterkte is
gedurende 2,6 ms hoger dan 34 A.
Bij een pulsduur van 2,5 ms is de huidweerstand dus blijkbaar ongeveer 50  (iets minder).
Conclusie: Door het aanbrengen van de gel wordt de huidweerstand 2 zo klein.
2.4
Serieschakeling
Kennisvragen
27 In een serieschakeling is de som van de spanning over de weerstanden gelijk aan de spanning
van de gebruikte spanningsbron. De stroom door elke weerstand is hetzelfde.
28 Bij een serieschakeling geldt dat de som van de spanningen over de weerstanden gelijk is
aan de spanning van de spanningsbron. Naarmate je meer weerstanden in serie schakelt,
komt over elke weerstand afzonderlijk een kleinere spanning te staan (de spanning wordt verdeeld!).
En een kleinere spanning geeft volgens U  I  R ook een kleinere stroomsterkte.
29 a Voor serieschakeling geldt: Rv = R1 + R2 + R3 dus Rv = 63 + 18 + 35 = 116 
b U  I  R  9,0  I  116  I 
9,0
 0,0776 A
116
c over 63 : Volgens U = I  R  U = 0,0776  63 = 4,89 V
over 18 : U = 0,0776 18 = 1,40 V
over 35 : U = 0,0776  35 = 2,72V
Controle: samen is het 9,0 V.
Afgerond: I = 0,078 A
Afgerond: U = 4,9 V
Afgerond: U = 1,4 V
Afgerond: U = 2,7 V
28
Newton havo deel 1
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
29
30 a De uitgangsspanning UPQ is gelijk aan de spanning over de weerstand van 10 k:
UPQ = I  R  UPQ = I  10103
Nieuwe onbekende: I.
9,0
. Nieuwe onbekende: Rv.
U b  I  R v  9,0  I  R v  I 
Rv
Je hebt hier te maken met serieschakeling: Rv = R1 + Rvar = 10 + 20 = 30 k
9,0
I
 0,30  10 3 A
30  10 3
UPQ = 0,3010-3  10103 = 3,0 V
Afgerond: UPQ = 3,0 V
b De totale weerstand in de kring neemt toe, daardoor neemt de stroomsterkte af.
UPQ = I  R  UPQ = I  10103 neemt dan ook af.
c Bij Rvar = 0  : UPQ = 9,0 V omdat de hele spanning van de spanningsbron dan
over de weerstand van 10 k staat.
9,0
Bij Rvar = 30 k: Rtotaal = R1 + Rvar = 10 + 30 = 40 k en I 
 0,225  103 A
3
40  10
Daarmee wordt UPQ = 0,22510-3  10103 = 2,25 V .
Afgerond: 2,3 V  U PQ  9,0 V
Oefenopgaven
34 Spanning instellen
a Zie de figuur hiernaast.
U
I
Het lampje moet een spanning van 6,0 V krijgen zodat
voor de weerstand UR = 12 - 6,0 = 6,0 V overblijft.
De stroomsterkte bij serieschakeling is hetzelfde:
6,0
IR = Ilamp = 0,50 A. Dus R 
Afgerond: R = 12 
 12,0 
0,50
6,0 V
0,50 A
b De weerstand kun je bepalen m.b.v. R 
35 Fietslampjes
R
+
-
12 V
koplamp
achterlicht
a Zie de figuur hiernaast.
b Bij serieschakeling is de stroomsterkte door beide lampjes gelijk.
Uit de diagrammen blijkt dat de koplamp bij een spanning
van 6,0 V een stroomsterkte heeft van ongeveer 470 mA.
Het achterlicht zou bij diezelfde spanning een stroomsterkte
van 46 mA moeten hebben. Aan deze waarden kan nooit
gelijktijdig voldaan worden bij serieschakeling.
+
-
c Het achterlicht zal het eerst doorbranden omdat bij het achterlicht het eerst de maximale toegestane
stroomsterkte wordt bereikt.
d Neem aan dat het achterlampje doorbrandt wanneer de spanning boven de 6,0 V komt, dus bij een
stroomsterkte van meer dan 46 mA. Bij die stroomsterkte zal de koplamp een spanning hebben van
ongeveer 0,4 V. De totale spanning over de twee lampjes in serie is dan dus 6,0 + 0,4 = 6,4 V.
2.5
Parallelschakeling
Kennisvragen
37 Bij een parallelschakeling staat over elke weerstand de spanning van de spanningsbron.
De som van de stroomsterktes door elke weerstand is gelijk aan de stroom die de spanningsbron
veroorzaakt.
38 Bij een parallelschakeling geldt dat de som van de stroomsterktes door de weerstanden gelijk is
aan de stroomsterkte die de spanningsbron veroorzaakt. Als je dus meer weerstanden parallel schakelt,
wordt de som van die stroomsterktes ook steeds groter: I = I1 + I2 + I3 + I4 + . . .
39 - Van overbelasting is sprake als de stroomsterkte door een leiding groter is dan de maximaal
toegestane stroomsterkte. De warmteontwikkeling in de leiding is dan te groot.
- Er sprake van kortsluiting wanneer de spanningsdraad en de nuldraad rechtstreeks met elkaar
in contact komen is. De weerstand is dan erg klein en de stroomsterkte daardoor erg groot.
- De huisinstallatie is op twee manieren beveiligd tegen overbelasting en kortsluiting: door middel van
een indeling in verschillende groepen en door middel van zekeringen: hoofdzekering en groepzekeringen.
Newton havo deel 1
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
30
40 a Parallel geschakeld: als één apparaat aan- of uitgeschakeld wordt, blijven de andere onveranderd
functioneren.
b In serie geschakeld: als het achterlicht wordt aangezet, gaat het controlelampje ook aan.
Bij uitschakelen gaat het ook weer uit.
c Parallel geschakeld: ze branden onafhankelijk van elkaar want als bijvoorbeeld het achterlicht kapot gaat,
blijft de koplamp gewoon branden.
41 a Voor parallelschakeling geldt:
1
1
1
1
1
1
1






 0,10  Rv  10 
Rv R1 R2 R3 63 18 35
Afgerond: Rv = 10 
N.B. Dit kun je gemakkelijk met je rekenmachine met de x-1-toets uitrekenen.
b U  I  R  9,0  I  10  I 
9,0
 0,90 A
10
Afgerond: I = 0,90 A
9,0
 0,143 A
63
9,0
 0,500 A
Bij 18 : I 
18
9,0
 0,257 A
Bij 35 : I 
35
(Controle: samen is het 0,90 A)
c Bij 63 :
I
Afgerond: I = 0,14 A
Afgerond: I = 0,50 A
Afgerond: I = 0,26 A
42 a R1 en R2 kun je vervangen door R12, er ontstaat een eenvoudige serieschakeling.
R12 kun je berekenen met de formule
Ub = 9,0 V
- +
1
1
1
voor parallelschakeling


R12 R1 R2
b
I
1
1
1


 0,0833  R12  12 
R12 20 30
50 
12 
Nu is er sprake van een serieschakeling van 12  en 50 
In serie opgeteld levert dit Rv = 62 
9,0
 0,1452 A
62
De spanning over de R3 = 50  is U = 0,145  50 = 7,26 V
c De hoofdstroom: U b  I  R v  9,0  I  62  I 
Afgerond: I = 0,15 A
Afgerond: U3 = 7,3 V
De spanning over R12 is U = 9,0 - 7,26 = 1,74 V
Afgerond: U12 = 1,7 V
Dit is dus ook de spanning over de parallel geschakelde weerstanden van 20 en 30 .
d De stroomsterkte door R3 is I = 0,145 A.
U1 = U2 = 1,74 V  de stroomsterkte door R1 = 20  is I1 
1,74
 0,087 A . Afgerond: I 1= 87 mA
20
1,74
 0,058 A .
Afgerond: I 1= 58 mA
30
Controle: I = I1 + I2 = 0,078 + 0,058 = 0,136 A.
Dit stemt niet overeen met het feit dat I3 = I1 + I2 . Bedenk echter dat bij ‘vroegtijdig afronden’
er kleine verschillen op kunnen treden!)
En de stroomsterkte door R2 = 30  is I2 
43 a Voor de vervangingsweerstand R12 van R1 en R2 geldt: R12 = R1 + R2 = 20 + 30 = 50 
Er is dan een eenvoudige parallelschakeling ontstaan.
b Er staan nu 2 weerstanden van 50  parallel, deze zijn te vervangen door 25 ,
want
1
1
1
1
1




 0,040  Rv  25  .
Rv R12 R3 50 50
c Voor de hoofdstroom geldt: Ub  Ih  Rv  12  Ih  25  Ih 
Door elke weerstand gaat dus 0,24 A (2 gelijke takken!).
d U1 = I1  R1  U1 = 0,24  20 = 4,8 V en
U2 = I2  R2  U2 = 0,24  30 = 7,2 V.
Controle: U = U1 + U2 = 4,8 + 7,2 = 12,0 V.
12
 0,48 A
25
Afgerond: Ih = 0,48 A
Newton havo deel 1
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
31
Oefenvragen
47 Feestverlichting
Bij 230 V moeten de lampen parallel staan.
De stroomsterkte verdeelt zich over de lampen:
16
er kunnen dan maximaal
= 53 lampen
0,30
gebruikt worden.
maximaal 53
lampen parallel
230 V~
Bij 12 V moeten de lampen in serie.
Nu wordt de spanning verdeeld over de lampen:
230
230 V~
er moeten dan minimaal
 19 lampen per tak
minimaal 20 lampen in serie
12
gebruikt worden.
Het maximale aantal is onbeperkt, ze branden dan echter wel erg zwak!
16
Bij gebruik van 19 lampen per serie kunnen dan wel
 32 series parallel geschakeld worden.
0,5
Dat zijn dan 608 lampen in totaal!
48 Fietsverlichting
a De twee lampjes moeten parallel staan (zie figuur hiernaast).
b Bij parallelschakeling brandt elk lampje afzonderlijk
op een spanning van 5,0 V. Met behulp van de diagrammen
is dan te bepalen dat Idynamo = 440 + 43 = 483 mA.
5,0 V~
koplamp
c De LED moet in de kring naar het achterlicht opgenomen
worden (serieschakeling).Zie figuur hiernaast.
achterlicht
LED
d Voor de spanningsverdeling in de kring van het achterlicht
U
R
geldt: LED  LED en Udynamo = ULED + Ua.
Ua
Ra
Voor de weerstand van de LED geldt: ULED  ILED  RLED 
0,30  0,05  RLED  RLED
5,0 V~
0,30

 6,0 
0,05
Evenzo geldt voor het achterlicht: Ra 
koplamp
achterlicht
5,0
 116  .
0,043
We nemen voor het gemak aan dat deze weerstandswaarde constant is.
U
6,0 0,052
De spanningsverhouding over LED en achterlicht wordt dan LED 
zijn.

Ua
116
1
Het spanningsdeel (van de 5,0 V) dat de LED krijgt, is dan: ULED 
0,052
 5,0  0,247 V  ULED  0,25 V .
1,052
Dit is dus wat minder dan de LED mag hebben.
e Door het aanbrengen van het controlelampje gaat er minder stroom door het achterlicht omdat
de weerstand van die tak iets groter is geworden: de dynamo hoeft iets minder stroom te leveren.
49 a Bij serieschakeling is er sprake van spanningsverdeling: U = U1 + U2 + U3 + … enz.
Hierbij is: U = I  Rv ; Rv = R1 + R2 + R3 + … enz. en U1 = I  R1 enz.
b Bij parallelschakeling is er sprake van van stroomverdeling: I = I1 + I2 + I3 (enz.).
1
1
1
1
Hierbij is: U1 = I  R1 (enz.). Daarnaast is
(enz.) en U = I  Rv .



Rv R1 R2 R3
c Om een combinatieschakeling door te kunnen rekenen, moet je deze eerst vereenvoudigen
tot een eenvoudige serie of parallelschakeling. Daarbij zoek je in de gegeven schakeling eerst
de vertakkingspunten. Tussen twee vertakkingspunten zoek je naar serie- en parallelschakelingen.
Op de gevonden serie- of parallelschakeling pas je vervolgens de gebruikelijke manier toe
om de verschillende grootheden te berekenen.
Newton havo deel 1
2.6
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
32
Elektrische energie en vermogen
Kennisvragen
51 Je kunt de spanning U over en de stroomsterkte I door het apparaat meten.
Vervolgens bereken je het vermogen m.b.v. Pe = U  I .
Een andere manier is dat je bijvoorbeeld met een kilowattuurmeter de verbruikte elektrische energie Ee meet
en omrekent in de eenheid J (=Joule). Daarnaast meet je de tijdsduur t.
E
Vervolgens bereken je het vermogen m.b.v. Pe  e .
t
52 Zie ook informatieboek.
Voorbeeld van filmprojector:
stralingsenergie
bewegingsenergie
elektrische
energie
warmte (motor en lamp)
warmte in snoer
53 Met energieverlies wordt bedoeld de warmteontwikkeling in leidingen en apparaten op plaatsen
waar je dat niet wilt.
54 a Pe  U  I  60  230  I  I 
60
 0,261A
230
b U  I  R  230  0,26  R  R 
230
 882 
0,26
Afgerond: I = 0,26 A
Afgerond: R = 8,8102 
c Als U 2x zo klein wordt, is I ook 2x zo klein, dus P wordt 4x zo klein:
P = 15 W.
55 a Gevraagd: De elektrische energie E (in kWh en J).
Gegeven: Pe = 60 W = 0,060 kW; t = 1000 uur = 1000  3600 = 3,600106 s.
Ee = Pe  t = 60  3,600106 = 2,16108 J
Afgerond: Ee = 2,2108 J = 2,2102 MJ
of Ee = Pe  t = 0,060  1000 = 60 kWh
Afgerond: Ee = 60 kWh
b De kosten zijn 60 maal de prijs van 1 kWh = 60  € 0,10 = € 6,00
56 a Gevraagd: Pe.
Gegeven: R = 23 ; U =230 V.
Pe = U  I = 230  I
Nieuwe onbekende: I.
230
U  I  R  230  I  23  I 
 10 A .
23
Pe = 230  10 = 2300 W
Afgerond: P = 2,3 kW.
b Gevraagd: De elektrische energie Ee (in kWh en J).
Gegeven: t = de kachel staat aan gedurende 10 + 5 + 7,5 + 7,5 = 30 min = 0,5 h = 1800 s;
Pe = 2,3 kW = 2,3103 W.
In Joule: Ee = Pe  t = 2,3103  1800 = 4,14106 J
Afgerond: E = 4,1106 J = 4,1 MJ
In kWh: Ee = Pe  t = 2,3  0,5 = 1,15 kWh.
Afgerond: E = 1,2 kWh
Newton havo deel 1
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
57 a Gevraagd: het vermogen Pe.
Gegeven: Ub = 24 V; R1 = 12 ; R2 = 48 
Pe = U  I = 24  I Nieuwe onbekende: I.
U = I  Rv  24 = I  Rv Nieuwe onbekende: Rv.
Rv = R1 + R2 = 12 + 48 = 60 
24
 0,40 A
24 = I  60  I 
60
Pe = 24  0,40 = 9,60 W
33
R1 =12 
+
R2 = 48 
-
Ub = 24 V
Afgerond: Pe = 9,6 W
b Bij parallel schakeling krijgt elke weerstand een spanning van 24 V. De vervangingsweerstand
is kleiner dan één van de twee gegeven weerstanden. De geleverde stroomsterkte I wordt dus groter.
Dit betekent dat geleverde vermogen ook groter wordt (want Pe = U  I).
Pe = U  I = 24  I Nieuwe onbekende: I.
U = I  Rv  24 = I  Rv Nieuwe onbekende: Rv.
1
1
1
1
1




 0,1042  R v  9,60 
Rv R1 R2 12 48
24
 2,5 A
9,6
Pe = U  I = 24  2,5 = 60 W
60
Het vermogen is dus
 6,25  zo groot.
9,6
24 = I  9,60  I 
Afgerond: 6,3 zo groot.
Oefenvragen
60 Kabelhaspel
a In opgerolde toestand is de warmteafgifte aan de omgeving minder. De isolatie kan sneller smelten.
b De stroomsterkte door de boormachine : Pe  U  I  400  230  I  I 
De stroomsterkte door de straalkachel : I 
400
 1,74 A . Wel aansluiten!
230
1000
 4,35 A . Dus niet aansluiten!
230
61 Wasmachine
a Er wordt niet voortdurend verwarmd. Ook draait de motor afwisselend de ene en de andere kant uit
waarbij deze tussen het afwisselen kort pauzeert.
b Om de elektriciteitskosten te bepalen moet je weten hoe groot het energiegebruik is in kWh,
want we nemen aan dat 1 kWh een bedrag van € 0,10 kost.
Gegeven: Pe = 2,4 kW en de tijdsduur t = 75 min = 1,25 uur.
Ee = Pe  t = 2,4  1,25 = 3,0 kWh
Kosten: 3,0  € 0,10 = € 0,30.
c Bij het maximumvermogen is de stroomsterkte als volgt te berekenen:
3200
Pe,max  U  Imax  3200  230  Imax  Imax 
 13,9 A
Afgerond: I = 14 A
230
Conclusie: je hebt een zekering van 16 A nodig.
62 Wasmachine/droger-combinatie
Gegeven is dat een wasmachine Pe,max = 3200 W heeft en de wasdroger Pe,max = 3300 W.
Samen is dat 5700 W.
5700
 24,78 A
De stroomsterkte is als volgt te bepalen: Pe,max  U  Imax  5700  230  Imax  Imax 
230
Afgerond: Imax = 25 A
Conclusie: Je kunt beide apparaten dus niet tegelijkertijd op een zekering van 16 A aansluiten.
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
Newton havo deel 1
34
63 Straalkachel
a Gevraagd: de weerstand R1 en R2.
Gegeven: Pe,R1 = P1 = 500 W; Pe,R2 = P2 = 1000 W; U = 230 V.
U
230
Nieuwe onbekende: I.
R 
I
I
P
Pe  U  I  Pe  230  I  I  e
230
1000
500
 4,35 A .
Invullen: I1 
 2,17 A ; I 2 
230
230
230
230
R1 
 105,8  ; R2 
 52,9  .
2,17
4,35
R1 : 0,50 kW
R2 : 1,0 kW
230 V~
Afgerond: R1 = 11101  R2 = 53 
b De twee verwarmingselementen staan parallel aan elkaar (zie figuur): voor een groter vermogen bij 230 V
moet I groter zijn want Pe = U  I. Dus R kleiner  parallel geschakeld.
c Gevraagd: warmteontwikkeling per seconde én verliespercentage van het geleverde elektrisch vermogen.
Gegeven: snoer ℓ = 5,0 m; R = 0,011 /m; Pe = 1,5103 W.
Voor het elektrisch vermogen dat wordt omgezet in warmteontwikkeling kun je gebruik maken van:
Pleiding = I2  Rleiding. Onbekend zijn: I en Rleiding.
1500
 6,52 A
230
Rleiding = 2  ℓ  weerstand per meter = 2  5,0  0,011 = 0,11 .
Pleiding = 6,522  0,11 = 4,68 W
Pe  U  I  1500  230  I dus I 
d Het verlies is 4,68 W op de 1500 W  procentueel:
Afgerond: Pleiding = 4,7 W
4,68
 100%  0,312%
1500
Afgerond: 0,31 %.
64 a Ee  Pe  t . De eenheid voor Pe is de watt en voor Ee de joule. Hierbij geldt: 1 W = 1 J/s.
b Uit Pe  U  I en U  I  R kun je afleiden dat Pe  I 2  R . De formule U = I  R wordt hierbij
gebruikt om de spanning U in de formule Pe = U  I te vervangen door I  R .
c Ee  U  I  t en Ee  I 2  R  t .
d In de formule Ee  I 2  R  t is R een constante grootheid. Als je voor de tijdsduur t ook een bepaalde
waarde kiest, dan blijft er over dat Ee evenredig is met I2 dus kwadratisch evenredig met I.
e De formule Ee  I 2  R  t laat zien dat Ee evenredig is met R als je uitgaat van een constante waarde
voor de stroomsterkte I en de tijdsduur t .
2.7
Weerstand
Kennisvragen
66 a De weerstand R neemt toe als de temperatuur T hoger wordt (zie figuur a).
b De weerstand R neemt toe als de lengte ℓ groter wordt:
de weerstand R is rechtevenredig met de lengte ℓ (zie figuur b).
c De weerstand R neemt af als de dwarsdoorsnedeoppervlakte A toeneemt:
de weerstand R is omgekeerd evenredig met de dwarsdoorsnedeoppervlakte A (zie figuur c).
figuur a
figuur c
figuur b
R
R
T
R
A
d De soortelijke weerstand  bepaalt de invloed van het draadmateriaal op de weerstand R.
De eenheid is m (eigenlijk: m2/m).
De waarden van deze grootheid vind je in één van de kolommen van tabel 8, 9 en 10.
Newton havo deel 1
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
67 Sluit de koperdraad aan op een spanningsbron, neem een ampèremeter op in de schakeling
om de stroomsterkte I te meten en bepaal met een voltmeter de spanning U over de koperdraad.
U
De weerstand kun je dan berekenen m.b.v. R  .
I
V
Met de weerstand, de lengte (meten) en de soortelijke weerstand
is de dwarsdoorsnedeoppervlakte te bepalen


A
want R   
 A .
koperdraad
A
R
2
Met A =   r is de straal van de draaddoorsnede te berekenen.
En vervolgens de diameter d = 2  r.
+ 68 Gevraagd: weerstand R.
Gegeven: constantaandraad met ℓ = 5,0 m en d = 0,2010-3 m.

Nieuwe onbekenden:  en A.
R
A
BINAS (tabel 9): constantaan = 0,4510-6 m.
A =   r 2 met r = ½ d = 0,1010-3 m  A =   (0,1010-3)2 = 3,1410-8 m²
5,0
Afgerond: R = 72 
R  0,45  10 6 
 71,6 
3,14  10 8
69 Gevraagd: soort metaal.
Gegeven: metaaldraad met ℓ = 0,80 m; A = 1,510-6 m²; R =9,110-3 .
Het soort metaal kun je vinden als je de soortelijke weerstand  zou kennen.

0,80
9,1  10-3  1,5  106
 9,1  10- 3   
dus


 17  10 9 m
A
0,80
1,5  10  6
Volgens BINAS (tabel 8) heb je dan te maken met het metaal koper.
R
70 Gegeven: Element ℓ = 0,124 m; U = 230 V; P = 1200 W.
a Pe  U  I  1200  230  I  I 
1200
 5,217 A
230
Afgerond: I = 5,22 A Het antwoord klopt.
b Gevraagd: R en diameter d.
230
U
R  . Voor de stroomsterkte I zie vraag a  R 
 44,08 
I
5,217
Afgerond: R = 44,1 
d = 2  r en A =   r 2 . Nieuwe onbekende: A.

0,124
0,124
R  
 44,08  0,72  10 6 
 A  0,72  10 6 
 2,02  10 9 m2
A
A
44,08
2,0210-9 =   r ²  r = 2,5410-5 m  d = 5,0810-5 m
Afgerond: d = 5,110-5 m.
71 Het diagram laat een kromme lijn zien die steeds minder sterk stijgt: als de spanning U toeneemt,
U
neemt de stroomsterkte minder sterk toe. Dit betekent dat volgens R 
de weerstand dus toeneemt.
I
Dit klopt met het feit dat bij een toenemende spanning en stroomsterkte er meer warmte ontwikkeld wordt
waardoor temperatuur en dus ook de weerstand van de gloeidraad toeneemt.
72 Gevraagd: Ee in kWh.
Gegeven: U = 230 V; ℓ = 45 m; A = 2,5 mm² = 2,510-6 m²; t = 4,5 h.
Ee = Pe  t  Ee = Pe  4,5
Nieuwe onbekende: Pe.
Pe = U  I  Pe = 230  I
Nieuwe onbekende: I.
U = I  R Nieuwe onbekende: R.

R
BINAS (tabel 9): nichroom = 1,1010-6 m
A
45
R  1,10  10 6 
 19,8 
2,5  10 6
230
 11,62 A
19,8
Pe = 230  11,62 = 2673 W = 2,673 kW
Ee = 2,673  4,5 = 12,0 kWh
230 = I  19,8  I 
Afgerond: Ee = 12 kWh
35
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
Newton havo deel 1
36
73 N.B. In dit geval kijk je naar de stroomkring van spanningsbron, variabele weerstand en vaste weerstand
van 100 . De parallelle kring met het lampje is verder niet van belang en zolang de schakelaar open staat
ook de weerstand van 100 k niet.
Gevraagd: Rvariabel = R1.
Gegeven: U = 9,0 V; R2 = 100 ; UAB = U2 = 1,2 V.
U1 = I1  R1 Nieuwe onbekenden: U1 en I1.
Ubron = U1 + U2 (serieschakeling)  9,0 = U1 + 1,2  U1 = 7,8 V
Aangezien de schakelaar in de horizontale verbinding open staat, geldt: I1 = I2
U
1,2
I2  2  I2 
 0,012 A  I1 = 0,012 A
R2
100
7,8 = 0,012  R1  R1 
7,8
 650 
0,012
Afgerond: R variabel = 6,510 2 
Oefenopgaven
81 Tl-buis
Gevraagd: .
Gegevens: U = 230 V; Pe = 9,0 W; d = 8,5 mm = 8,510-3 m ; ℓ = 0,40 m.

Nieuwe onbekenden: R en A.
R 
A
U
Nieuwe onbekende: I.
R
I
9,0
 0,0391A
Pe  U  I  9,0  230  I  I 
230
230
R
 5878 
0,0391
A =   r² waarbij r = ½ d = 4,2510-3 m  A = 56,710-6 m2
5878   
0,40
56,7  10
6
 
5878  56,7  10  6
 0,834 m
0,40

Afgerond:  = 0,83 m
82 Kortsluiting
Gevraagd: Ikortsluiting = Ik.
Gegeven: U = 230 V; ℓ = 2  10 = 20 m ; A = 2,5 mm² = 2,510-6 m².
U = Ik  R Nieuwe onbekende: R.

Nieuwe onbekende: koper .
R
A
BINAS (tabel 8): koper = 1710-9 m
20
R  17  10 9 
 0,136 
2,5  10 6
230
230  I k  0,136  I k 
 1691A
0,136
Afgerond: Ik = 1,7103 A.
83 Hoogspanningsleiding
Gevraagd: Q = E (verlies) per seconde?
Welk percentage is dit van het geleverde elektrische vermogen Pe?
Gegeven: koperdraad; ℓ = 2  25 = 50 km = 50103 m; A = 2,5 mm² = 2,510-4 m²;
Pc = 80 MW = 80106 W; Uc = 380 kV = 380103 V.
2
Q= E e = I  Rdraad  t Hierbij is de tijdsduur t = 1 s (per seconde !).
Nieuwe onbekenden: I en Rdraad.
Pc  Uc  I  80  106  380  103  I  I 
80  106
380  103
 210,5 A

Nieuwe onbekende: 
A
BINAS (tabel 8):  koper = 1710-9 m
Rdraad   
R  17  10  9 
50  103
 3,4 
2,5  10  4
Q = E (verlies) = 210,52  3,4  1 = 1507103 J = 0,151 MJ
0,0151
 100 % = 0,188 %     
In procenten:
80
Afgerond: Q = 0,15 MJ




Afgerond: Verlies = 0,19 %
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
Newton havo deel 1
2.9
37
Afsluiting
Oefenopgaven
RAP = ?
A
87 Bovenleiding
Oriëntatie:
Gevraagd: deel van vermogen dat verloren
gaat door warmteontwikkeling in bovenleiding (RAP)
en in de rails (RPA).
Gegeven: zie figuur.
Hypothese: Het vermogen dat verloren gaat,
zal waarschijnlijk niet erg groot zijn
Planning:
De gevraagde warmteontwikkeling
per seconde kun je schrijven als Q = Pe, AP + Pe, PA.
Het verbruikte vermogen is Pe,bron en
Q
gevraagd wordt naar de verhouding
.
Pe,bron
P
I = 300 A
AP = 2,6.103 m
koperdraad met
A = 3,1.10- 4 m2
M
U = 1500 V
A
P
RPA = 0,044 
De twee grootheden die dus bepaald moeten worden, zijn Pe, bron en Q.
Het vermogen Pe bron = U  I
 U en I zijn beide gegeven.
M.b.v. U = I  R is het elektrische vermogen ook te schrijven als Pe = I2  R
Aangezien je te maken hebt met een serieschakeling is de stroomsterkte I overal hetzelfde
dus Q = I2  ( RAP + RPA)

De weerstand RPA is gegeven en de weerstand RAP kun je uitrekenen met R    .
A
l en A zijn gegeven en de soortelijke weerstand koper kun je opzoeken
in BINAS (tabel 8):  = 1710-9 m.
Uitvoering:
RAP   

2,6  103
 17  10 9 
 0,143  en Rtotaal = RAP + RPA = 0,143 + 0,044 = 0,187 
A
3,1 10 4
Q = 3002  (0,187) = 16 830 W = 16,83 kW
Pe,bron = 1500  300 = 4,50105 W = 450 kW
Q
16,83

 0,0374
Pe,bron
450
Afgerond: 0,037 of 3,7 %
Controle:
Wat je in ieder geval weet is dat het deel altijd kleiner moet zijn dan 1 (of kleiner dan 100 %).
3,7 % is ook geen extreem hoog percentage.
Newton havo deel 1
Uitwerkingen hoofdstuk 2 – De elektrische huisinstallatie
88 Bovenleiding bij dubbelspoor
Oriëntatie:
Gevraagd: wordt het vermogen nu kleiner?
Gegevens: zie schakelschema in de figuur hiernaast.
Hypothese: door het gebruik maken van
de andere bovenleiding maak je gebruik van
parallel-schakeling van weerstanden.
De vervangingsweerstand wordt dan kleiner
dan de eerder berekende 0,143  in opg. 87.
De stroomsterkte blijft hetzelfde dus zal
de warmteontwikkeling per seconde
dan ook kleiner zijn.
38
ABP = 4,5.103 + (4,5 - 2,6).103 = 6,4.103 m
koperdraad met A = 3,1.10 - 4 m2
A
B
A
P
P
RAP = 0,143 
I = 300 A
M
U = 1500 V
Conclusie: het vermogensverlies is kleiner.
N.B.
A
Hoe het antwoord hierboven al gegeven is
kun je het ook nog quantitatief bewijzen d.w.z. m.b.v. een berekening.
Q
Dus stel dat gevraagd werd: hoe groot is
?
Pe,bron
P
Planning:
Het vermogen Pe bron = U  I blijft hetzelfde omdat zowel de spanning U
als de hoofdstroom I hetzelfde blijven.
Q = Pe, verv. + Pe, AP = I2  (Rv + RAP )
De weerstand RAP van de bovenleiding is nu een parallelschakeling van twee weerstanden.
1
1
1
De vervangingsweerstand is te berekenen met behulp van:
,


Rv RAP RABP
waarbij RABP nog berekend moet worden m.b.v. R ABP   

.
A
Uitvoering:
R ABP   
6,4  103

 RABP  17  10 9 
 0,351
A
3,1 10 4
1
1
1


 9,842  Rv  0,102 
Rv 0,351 0,143
Q = 3002  (0,102 + 0,044) = 13104 W = 13,104 kW
Pe,bron = 1500  300 = 4,50105 W = 450 kW
Q
13

 0,0288
Pe,bron
450
Afgerond: 0,029 of 2,9 %
Controle:
Het deel van het vermogen, dat aan warmteontwikkeling in bovenleiding en rails verloren gaat,
is inderdaad kleiner geworden.