Bijlage bij MBO-keuzedeel Beschrijving van de

Bijlage bij MBO-keuzedeel
Voorbereiding HBO Wiskunde voor de techniek
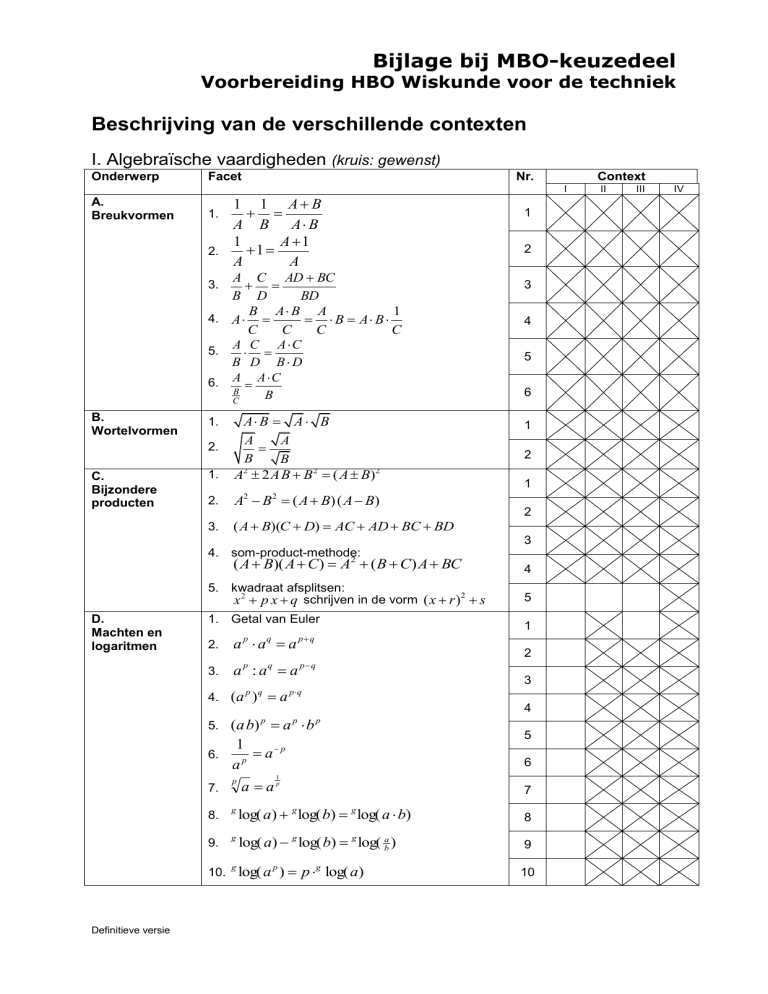
Beschrijving van de verschillende contexten
I. Algebraïsche vaardigheden (kruis: gewenst)
Onderwerp
Facet
Nr.
Context
I
A.
Breukvormen
1 1 A B
 
A B A B
1
A 1
1 
2.
A
A
1.
A C AD  BC
 
B D
BD
B A B A
1
4. A  
  B  A B 
C
C
C
C
A C AC
5.
 
B D BD
6. A  A  C
B
B
C
3.
B.
Wortelvormen
1.
A B  A  B
A
A

B
B
A2  2 A B  B2  ( A  B)2
2.
A2  B2  ( A  B) ( A  B)
3.
( A  B)(C  D)  AC  AD  BC  BD
1.
2.
C.
Bijzondere
producten
1
2
3
4
5
6
1
2
1
2
3
4. som-product-methode:
2
D.
Machten en
logaritmen
( A  B)( A  C )  A  ( B  C ) A  BC
4
5. kwadraat afsplitsen:
x 2  p x  q schrijven in de vorm ( x  r )2  s
5
1. Getal van Euler
a a  a
3.
a p : aq  a p q
4.
(a )  a
q
p q
5.
7.
Definitieve versie
p
a a
2
3
pq
4
(a b)  a  b
1
 a p
6.
ap
p
1
pq
2.
p
p
p
1
p
5
6
7
8.
g
log( a)  g log( b)  g log( a  b)
8
9.
g
log( a)  g log( b)  g log( ba )
9
10.
g
log( a p )  p g log( a)
10
II
III
IV
Onderwerp
Facet
Nr.
Context
I
p
log( a)
log( g )
ln( a)
12. g log( a) 
ln( g )
11.
E.
Goniometrie
g
log( a) 
11
p
12
1. sin(-x) = - sin(x)
1
2. cos(-x) = cos(x)
2
2
2
3. sin x + cos x = 1
3
4. sin(x) = cos(½π – x)
4
5. sin(2 x) = 2 sin(x)cos(x)
5
2
F. 'Herleidingen'
uitvoeren aan de
hand van de
elementen genoemd
bij A - E
G.
Vergelijkingen
oplossen met
behulp van
algemene vormen
6. cos(2 x) = 2 cos (x) – 1
6
1. via substitutie van getallen
1
2. via substitutie van expressies
2
3. via het omwerken van formules
3
1.
A  B  0  A  0 of B  0
2.
A  B  A  C  A  0 of B  C
3.
A B  A C , A  0  B  C
A
 C  A  B  C , met B  0
4.
B
A C
  A  D  B  C , met B, D  0
5.
B D
6.
A2  B2  A  B of A   B
7.
A  B  A  B2
1.
f (a x  b)  d  e
behulp van
standaardfuncties
en transformaties
2.
f ( A)  f ( B)
I.
Vergelijkingen
oplossen via
algoritmen
1. eerstegraadsvergelijkingen
H.
Vergelijkingen
oplossen met
2
3
4
5
6
7
1
2
a x  b  0  x   ba
2. tweedegraadsvergelijkingen, abc-formule
a x2  b x  c  0  x 
b  b2  4 a c
2a
1
1
2
3.
xn  c  x  c n
3
4.
g x  a  x  g log( a)
4
5.
e x  a  x  ln(a)
5
6.
7.
Definitieve versie
1
g
log( x)  b  x  g b
6
7
ln( x)  b  x  eb
2
II
III
IV
K.
Vergelijkingen
en ongelijkheden van het type
1.
f ( x)  g ( x) grafisch
1
2.
f ( x)  g ( x) exact
2
3.
f ( x)  g ( x) grafisch
3
4.
f ( x)  g ( x) exact
4
II. Functies en Grafieken (kruis: gewenst)
Onderwerp
Facet
Nr.
Context
I
L.
Formule
opstellen
1. van een standaardfunctie
a. eerstegraads/lineaire functie
1a
b. tweedegraadsfunctie
1b
c. exponentiële functie
1c
d. logaritmische functie
1d
e. goniometrische functie
1e
f. machtsfunctie
1f
2. door generaliseren via getallenvoorbeelden
3. door schakelen van formules
2
3
M.
Expressies
herkennen
N
Karakteristieken
bepalen
O.
Algebraïsche
expressies
reduceren en
representeren
Definitieve versie
1. vaststellen of een (deel)expressie behoort tot
een van de volgende families
a. eerstegraads/lineaire functies
1a
b. tweedegraadsfuncties
1b
c. exponentiële functies
1c
d. logaritmische functies
1d
e. goniometrische functie
1e
f. machtsfuncties
1f
2. structuur van een expressie vaststellen
2
3. rol van een voorkomende parameter bepalen
3
kwalitatief redeneren over expressies of delen
daarvan met betrekking tot karakteristieken als
1. uiterste waarden
1
2. stijgen of dalen
2
3. symmetrie
3
4. asymptotisch gedrag
4
1. complexe delen van een expressie
vervangen door 'plaatsvervangers' zodat
herkenbare expressies ontstaan
2. flexibel kunnen wisselen tussen betekenis
toekennen aan symbolen en betekenisloos
kunnen manipuleren
3. flexibel verschillende representaties van
functies (formule, tabel, grafiek) kunnen
inzetten en tussen deze representaties
kunnen wisselen
3
1
2
3
II
III
IV
III. Meetkunde (kruis: gewenst)
Onderwerp
Facet
Nr.
Context
I
P.
Vlakke
meetkunde
1. In meetkundige, contextrijke toepassingen
afstanden tussen een punt en een lijn en
hoeken tussen lijnen kunnen bepalen
2. de stelling van Pythagoras kennen en
kunnen toepassen
3. de sinus- en cosinusregel kennen en
kunnen toepassen.
II
III
IV
1
2
3
IV. Differentiaalrekening (kruis: gewenst)
Onderwerp
Facet
Nr.
Context
I
Q.
Begrip afgeleide
R.
Rekenen aan
afgeleiden
S.
Toepassen
1. het begripsmatig en routinematig kunnen
omgaan met het begrip afgeleide van een
(strandaard)functie als maat voor de
verandering van een functiewaarde in een
bepaald punt
1. De som-. product- en quotiëntregel kunnen
toepassen op eenvoudige enkelvoudige functies
2. de kettingregel kunnen toepassen op
eenvoudige samengestelde functies
1
1. binnen een beroepscontext begrippen als
toename, snelheid, groei en gradiënt wiskundig
kunnen beschrijven en hanteren
2. realistische optimaliseringproblemen kunnen
opstellen en oplossen.
3. Het vermogen om rekenkundige, algebraïsche
en deductieve vaardigheden te kunnen
uitvoeren zonder ICT.
1
II
III
IV
1
2
2
3
V. Modelleren (kruis: gewenst)
Onderwerp
Facet
Nr.
Context
I
T.
Definitieve versie
1. Het kunnen vertalen van technische
probleemsituaties in wiskundige termen, deze
(wiskundige) problemen kunnen analyseren en
kunnen oplossen, en het resultaat naar de
betreffende technische context kunnen
terugvertalen.
2. Het kunnen vertalen van economische
probleemsituaties in wiskundige termen, deze
(wiskundige) problemen kunnen analyseren en
kunnen oplossen, en het resultaat naar de
betreffende economische context kunnen
terugvertalen.
4
1
2
II
III
IV