Opgave 4 Onderzoek aan een lichtsensor (havo – na1,2 – 2001

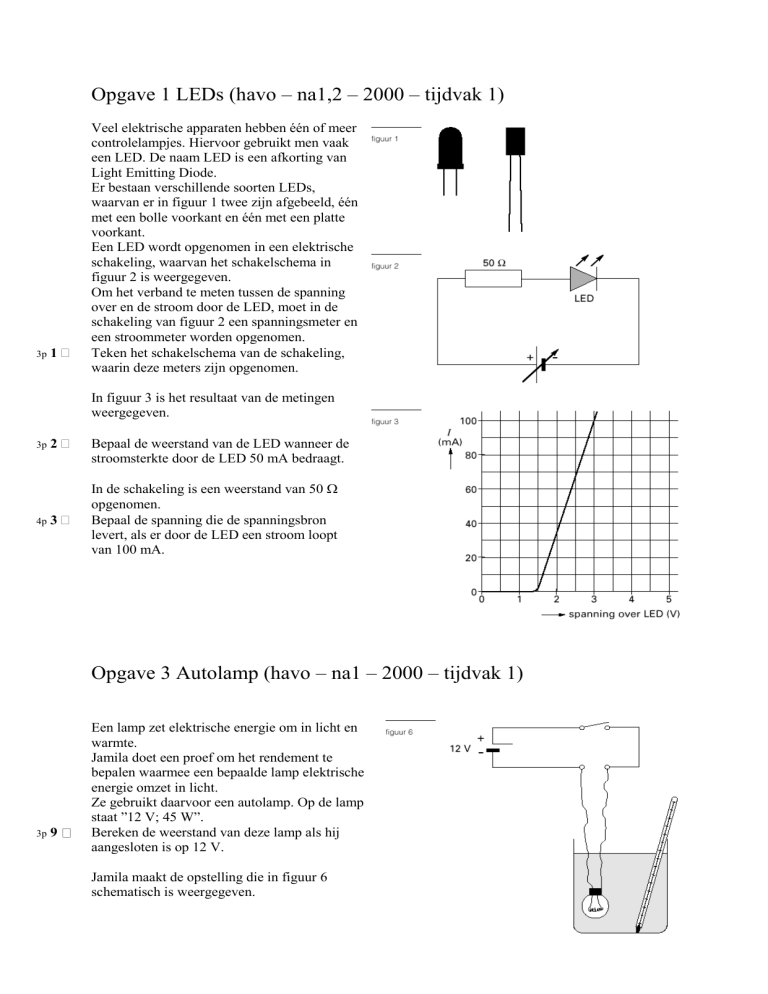
Opgave 1 LEDs (havo – na1,2 – 2000 – tijdvak 1)
3p
1
Veel elektrische apparaten hebben één of meer
controlelampjes. Hiervoor gebruikt men vaak
een LED. De naam LED is een afkorting van
Light Emitting Diode.
Er bestaan verschillende soorten LEDs,
waarvan er in figuur 1 twee zijn afgebeeld, één
met een bolle voorkant en één met een platte
voorkant.
Een LED wordt opgenomen in een elektrische
schakeling, waarvan het schakelschema in
figuur 2 is weergegeven.
Om het verband te meten tussen de spanning
over en de stroom door de LED, moet in de
schakeling van figuur 2 een spanningsmeter en
een stroommeter worden opgenomen.
Teken het schakelschema van de schakeling,
waarin deze meters zijn opgenomen.
In figuur 3 is het resultaat van de metingen
weergegeven.
3p
4p
2
3
Bepaal de weerstand van de LED wanneer de
stroomsterkte door de LED 50 mA bedraagt.
In de schakeling is een weerstand van 50 
opgenomen.
Bepaal de spanning die de spanningsbron
levert, als er door de LED een stroom loopt
van 100 mA.
Opgave 3 Autolamp (havo – na1 – 2000 – tijdvak 1)
3p
9
Een lamp zet elektrische energie om in licht en
warmte.
Jamila doet een proef om het rendement te
bepalen waarmee een bepaalde lamp elektrische
energie omzet in licht.
Ze gebruikt daarvoor een autolamp. Op de lamp
staat ”12 V; 45 W”.
Bereken de weerstand van deze lamp als hij
aangesloten is op 12 V.
Jamila maakt de opstelling die in figuur 6
schematisch is weergegeven.
2p
10
In het bekerglas heeft zij gedestilleerd water gedaan.
Leg uit waarom zij gedestilleerd water gebruikt en geen leidingwater.
Opgave 1 Slijtage bovenleiding (havo – na1 – 2000 – tijdvak 2)
Tegenwoordig is in Nederland 5200 km van het spoor geëlektrificeerd. De elektrische treinen die over
dat spoor rijden, krijgen hun stroom via de zogenaamde bovenleiding.
Deze bovenleiding bestaat uit twee koperen draden naast elkaar. Zie figuur 1.
4p
1
4p
2
3p
3
Tijdens het rijden schuurt de stroomafnemer
die aan de trein vastzit langs de twee
koperdraden. Daardoor slijten de draden af. In
figuur 2 zijn de doorsneden van een nieuwe
draad A en een afgesleten draad B getekend.
De doorsnede van draad A heeft een
oppervlakte van 98,8 mm2 en die van draad B
78,7 mm2. Stel dat de hele bovenleiding van
Nederland bestaat uit twee parallelle draden van het type A en na verloop van tijd (ongeveer 25 jaar) is
afgesleten tot draden van het type B.
De massa van 1,0 m3 koper is 8,96103 kg.
Bereken de massa van het koper dat op deze manier van de bovenleiding is afgesleten.
Bereken de weerstand van 1,0 km van zo’n afgesleten bovenleiding, bestaande uit twee parallelle
draden van het type B.
Ten gevolge van de elektrische stroom wordt in elke meter bovenleidingdraad een bepaalde
hoeveelheid warmte per seconde ontwikkeld.
Leg uit of, bij een zelfde stroomsterkte, in één meter draad van het type B meer of minder warmte per
seconde wordt ontwikkeld dan in één meter draad van het type A.
Opgave 4 Afwasmachine (havo – na1 – 2000 – tijdvak 2)
Anneke wil een nieuwe afwasmachine kopen en raadpleegt daarvoor een artikel in een
consumentenblad. Dat bevat een tabel met de uitkomsten van een vergelijkend onderzoek. Zie tabel 1.
Met de kennis uit de tabel gaat ze naar een winkel. Een verkoper vertelt haar dat het bedrag dat je per
jaar aan energie betaalt voor het afwassen met een afwasmachine bij normaal gebruik beneden de
100 gulden ligt. Neem aan dat je eenmaal per twee dagen afwast en dat 1 kWh 31 cent kost.
3p
13 
Ga met behulp van de tabel na of de bewering van de verkoper juist of onjuist is. Licht je antwoord toe
met een berekening.
Anneke gaat onderzoeken hoe het precies zit met het energieverbruik van de AEG FAVORIT 8080 I.
Tijdens een afwasbeurt meet ze met een vermogensmeter het vermogen van het apparaat als functie
van de tijd. Zie de grafiek van figuur 5. De netspanning is 230 V.
3p
15 
Bepaal de grootte van de stroomsterkte tijdens het verwarmen van het water bij het wassen.
3p
3p
16 
17 
Bepaal met behulp van de grafiek welk van de drie onderdelen, ’voorspoelen’, ’wassen’ of
’afspoelen en drogen’ de meeste energie kost.
Anneke wil het afwassen met een afwasmachine vergelijken met het afwassen met de hand.
Als onderzoeksvraag stelt zij:
„Bij welke manier van afwassen wordt de minste energie verbruikt, bij het afwassen met een
afwasmachine of bij het afwassen met de hand?”
Zij gaat door metingen de energie bepalen die bij het afwassen met de hand verbruikt wordt.
Vervolgens vergelijkt zij dit met de energie die de vaatwasmachine volgens het consumentenblad
verbruikt. Bij haar onderzoek laat zij de arbeid die ze zelf met haar handen verricht buiten
beschouwing.
Beschrijf wat zij moet meten om de onderzoeksvraag te beantwoorden.
Opgave 3 Ontdooitransformator (havo – na1,2 – 2001 – tijdvak 1)
In de winter kan bij strenge vorst het water in de waterleidingen bevriezen. We zeggen dan dat 'de
waterleiding bevroren is'. Om bevroren leidingen te ontdooien kun je gebruik maken van een
zogenaamde ontdooitransformator. Zie figuur 2. De werking van dit apparaat wordt in onderstaand
artikel beschreven. Het artikel bevat tevens enkele gegevens over de ontdooitransformator.
artikel
Ontdooitransformator
Waterleidingbedrijven en installateurs
hebben hun handen vol aan bevroren
waterleidingen. Wanneer het om bevroren
metalen
leidingen
gaat,
is
de
ontdooitransformator het aangewezen
redmiddel; dat werkt altijd. Door de te
ontdooien leiding wordt een hoge
elektrische stroom gestuurd. In principe
kun je hiervoor iedere willekeurige
transformator gebruiken, als hij maar
voldoende vermogen heeft en werkt met
lage, ongevaarlijke spanning.
Er
is
nu
een
praktische
ontdooitransformator op de markt waarbij
je zelf de secundaire spanning kan
aanpassen aan de lengte en dikte van de
te ontdooien leiding. De transformator is
geheel in kunsthars gegoten en heeft een
gat in het midden. De secundaire
windingen maak je door een kabel een
aantal malen door het gat te halen.
Om één meter bevroren koperen leiding in
een redelijke tijd te ontdooien, moet de
ontdooitransformator
een
vermogen
leveren van ongeveer 400 watt; de
gebruikelijke secundaire spanning ligt
tussen de 4 en 8 volt. Deze spanning zet
je op de leiding door de kabel op een
bevroren gedeelte van de leiding te
klemmen. De kabel moet echter wel een
lagere weerstand hebben dan de leiding.
Een dikke laskabel bijvoorbeeld is zeer
geschikt.
naar: Technisch Weekblad, 15-01-1997
3p
3p
10
12
In het artikel staat dat de weerstand van de kabel die op de leiding wordt geklemd klein moet zijn
vergeleken met de weerstand van de leiding. In dat geval wordt er in de kabel relatief weinig en in de
te ontdooien leiding juist veel warmte ontwikkeld.
Leg uit dat dan in de leiding meer warmte wordt ontwikkeld dan in de kabel. Gebruik bij je uitleg een
formule.
Het maakt verschil of een koperen leiding of een aluminium leiding ontdooid moet worden. De twee
leidingen hebben dezelfde afmetingen. Neem aan dat in beide gevallen de spanning tussen de
klemmen op de leiding even groot is.
Leg met behulp van het begrip soortelijke weerstand uit dat het ontdooien van het ijs in een koperen
leiding korter duurt dan het ontdooien van het ijs in een even lang stuk aluminium leiding.
Opgave 4 Onderzoek aan een lichtsensor (havo – na1,2 – 2001 – tijdvak 1)
Maaike en Lia onderzoeken hoe de weerstand van een LDR afhangt van de verlichtingssterkte.
Daartoe hangen ze een gloeilamp boven de LDR in een voor de rest verduisterde ruimte. Ze variëren
de afstand tussen de lamp en de LDR. Bij elke afstand meten ze de weerstand van de LDR.
Van de resultaten van de proef maken ze een grafiek die is weergegeven in figuur 3.
2p
13
Leg met behulp van figuur 3 uit of de weerstand van de LDR groter of kleiner wordt als de
verlichtingssterkte toeneemt.
Vervolgens maken ze de schakeling die in
figuur 4 is afgebeeld.
Voor de grootte van de weerstand R kan
gekozen worden uit een weerstand van 100 
en een weerstand van 500 .
3p
14
Leg uit bij welke van deze twee weerstanden (R = 100  of R = 500 ) de spanningsmeter de grootste
spanning aangeeft, als op de LDR eenzelfde hoeveelheid licht valt.
Opgave 6 Stadionverlichting (havo – na1,2 – 2001 – tijdvak 1)
In stadions worden speciale lampen gebruikt
voor de verlichting van het veld. Deze
lampen hebben drie minuten nodig om op te
starten. Tijdens het opstarten veranderen
zowel de spanning over als de stroom door
de lamp.
Pas na het opstarten bereiken de spanning en
de stroom hun constante eindwaarden. Zie
het diagram van figuur 8.
De percentages op de verticale as van deze
figuur zijn bepaald door de waarde van de
stroom (en de spanning) op een bepaald
tijdstip te vergelijken met de eindwaarde van
de stroom. I = 140% betekent dus dat de
stroom op het betreffende tijdstip 1,40 maal
zo groot is als de eindwaarde van de stroom.
Als de lamp na het opstarten goed brandt, is zijn vermogen 1800 W.
4p
3p
20
21
Bepaal het vermogen van de lamp op t = 1,0 minuut. Geef de uitkomst in twee significante cijfers.
Voor het verlichten van een bepaald stadion worden 228 van deze lampen gebruikt.
De hoeveelheid licht die een lamp per seconde geeft, wordt gemeten in de eenheid lumen.
Elke lamp in het stadion geeft 84 lumen licht voor elke watt elektrisch vermogen. Om een idee te
krijgen van de hoeveelheid licht die deze lampen geven, willen we uitrekenen hoeveel gloeilampen
van 100 W nodig zijn om het veld op dezelfde manier te verlichten.
Gloeilampen hebben een lager rendement dan de stadionlampen: een gloeilamp met een vermogen van
100 W geeft 14 lumen per watt elektrisch vermogen.
Bereken hoeveel van zulke gloeilampen nodig zijn om in het stadion dezelfde hoeveelheid licht te
krijgen als met de 228 stadionlampen.
Opgave 3 Vuurtoren (havo – na1 – 2001 – tijdvak 2)
4p
11
Het licht van een vuurtoren moet op grote afstand gezien kunnen worden. De lichtbundel moet dus een
grote intensiteit hebben. De lamp van de Brandaris op Terschelling is in 1920 speciaal voor
vuurtorens ontworpen. De gloeidraad van de lamp is van wolfraam, heeft een diameter van 0,35 mm
en een weerstand van 1,6 .
Bereken de lengte van de gloeidraad.
Opgave 1 Binnenverlichting (havo – na1,2 – 2002 – tijdvak 1)
4p
1
Bij een bepaald type auto bestaat de binnenverlichting uit twee parallel geschakelde lampjes. De
lampjes zijn aangesloten op de 12 V-accu van de auto. Elk lampje heeft bij die spanning een vermogen
van 5,0 W.
Bereken de weerstand die de binnenverlichting dan heeft.
Opgave 1 Automatisch fietsachterlicht (havo – na1,2 – 2002 –tijdvak 2)
Lees eerst het artikel.
artikel
Zelf de fietsdynamo aanzetten en
achterom kijken of het achterlicht wel
brandt, is er niet meer bij in de 21ste
eeuw. Want de AXA Omega 1 brandt
vanzelf; je hebt er geen omkijken naar.
Hoe dat kan? De Omega 1 heeft een
lichtsensor en een bewegingssensor.
Wordt het donker en beweegt de fiets,
dan gaat het achterlicht vanzelf branden.
Drie LED-lampjes zorgen voor een flinke
lichtopbrengst en ze zijn nog zuinig ook.
De Omega 1 brandt op twee penlightbatterijen van elk 1,5 V.
naar: De Kampioen
Navraag bij de fabrikant leverde de volgende gegevens op:
- De twee batterijen leveren samen een spanning van 3,0 V.
- De drie LED-lampjes zijn in serie geschakeld.
- Het vermogen van één LED bedraagt 70 mW.
3p
1
3p
2
3p 3
In de figuur op de bijlage zijn de twee batterijen en de drie LED-lampjes schematisch weergegeven.
De LEDjes zijn voor het gemak als gewone lampjes voorgesteld.
Teken in de figuur de verbindingsdraden zodat een schakeling ontstaat die voldoet aan de gegevens
van de fabrikant.
Bereken de stroomsterkte door een LED-lampje.
Het achterlicht kan 20 uren branden op de twee batterijen.
Bereken hoeveel energie de batterijen dan hebben geleverd.
Opgave 1 Verwarmingslint (havo – na1,2 – 2003 – 1)
In de winter zorgen bevroren waterleidingen
voor problemen. Er is nu een verwarmingslint
op de markt dat bevriezing voorkomt door de
leidingen te verwarmen. Het lint wordt
vastgezet op de waterleiding en aangesloten
op een stopcontact. Zie figuur 1.
Het lint geeft niet bij elke temperatuur
evenveel warmte af. In figuur 2 is
weergegeven hoe het vermogen van één meter
lint afhangt van de buitentemperatuur.
2p
1
Het is aan te bevelen om buiten het winterseizoen de stekker van het verwarmingslint uit het
stopcontact te halen.
Leg met behulp van figuur 2 uit waarom dit aan te bevelen is.
4p
2
De spanning van het lichtnet is 230 V.
Bepaal de weerstand van een lint van één meter als de buitentemperatuur -24 °C is.
Het lint bestaat uit de volgende onderdelen
(zie figuur 3):
- twee koperdraden;
- een zogenoemde zelfregelende kern die de
enige verbinding vormt tussen deze twee
draden;
- een omhulling voor de elektrische isolatie.
Het principe van de werking is als volgt:
Via de zelfregelende kern kunnen kleine elektrische stroompjes tussen de ene draad en de andere
lopen. Onder invloed van de temperatuur rangschikt het materiaal van de kern zich anders en zijn er
meer of minder parallelle, geleidende verbindingen. Zie de figuren 4A en 4B. De weerstand van de
koperdraden is verwaarloosbaar klein. De weerstand die elk van de elektrische stroompjes in de
zelfregelende kern ondervindt, is daarentegen groot.
3p
3
3p
4
In figuur 4 zijn twee situaties weergegeven.
Leg met behulp van bovenstaande informatie uit welke situatie, A of B, bij een lage buitentemperatuur
hoort.
Voor een langere waterleiding is een langer verwarmingslint nodig.
Leg uit of de weerstand van een verwarmingslint met een lengte van 2 meter groter is dan, kleiner is
dan of gelijk is aan de weerstand van een lint met een lengte van 1 meter. Neem daarbij aan dat de
temperatuur van beide linten gelijk is.
Opgave 3 Batterijen (havo – na1 – 2003 – tijdvak 2)
Op een batterij staat behalve de spanning die hij
levert, vaak ook de zogenaamde 'capaciteit'
vermeld.
De batterij die in figuur 6 is afgebeeld, levert
een spanning van 1,24 V en heeft een capaciteit
van 1,2 Ah.
Met de 'capaciteit' van een batterij wordt
bedoeld het product van de stroomsterkte die
van de batterij gevraagd wordt en de tijdsduur
waarin hij deze stroom kan leveren.
Dat wil zeggen dat een 'volle' batterij met
een capaciteit van l,2 Ah gedurende l0 uur een
stroomsterkte kan leveren van 0,12 A of
gedurende 20 uur een stroomsterkte van 0,06 A,
enzovoort. Na het afgeven van deze l ,2 Ah
daalt de stroomsterkte snel en is de batterij leeg.
4p
11 
De afgebeelde batterij zat in een elektrische klok. Na 250 dagen was de batterij leeg.
Bereken het vermogen van deze klok.
Er zijn ook batterijen waarop de capaciteit niet is vermeld.
Van zo'n batterij wil Hidde de capaciteit bepalen door te meten hoe lang de batterij een bepaalde
stroomsterkte kan leveren.
Hij maakt daarvoor een schakeling bestaande uit een volle batterij, een ampèremeter en een gloeilamp.
Zie figuur 7.
2p
12 
Teken in de figuur alle noodzakelijke verbindingsdraden.
In figuur 8 staat de grafiek die Hidde van zijn metingen heeft gemaakt.
3p
13 
Bepaal met behulp van figuur 8 de capaciteit van de onderzochte batterij.
In sommige apparaten schakelt men batterijen in serie, in andere apparaten zijn de batterijen parallel
geschakeld.
Hidde wil onderzoeken wat het effect hiervan is.
Daarvoor bouwt hij drie schakelingen. Zie figuur 9.
In de drie schakelingen sluit hij hetzelfde lampje aan.
3p
14 
Leg uit of het lampje in schakeling B feller of minder fel brandt dan in schakeling A of juist even fel.
3p
15 
Leg uit of het lampje in schakeling C langer of korter brandt dan in schakeling A of juist even lang.