4 HAVO wiskunde B – oefentoets hoofdstuk 6

4 HAVO wiskunde B – oefentoets hoofdstuk 6 – #eXp2016
Opgave 1
Gegeven is de functie f ( x ) 
1 3 1 2
x  x  x  1.
3
2
a. Punt A ligt op het snijpunt van de grafiek met de y-as.
Stel een vergelijking op van de raaklijn aan de grafiek van f door het punt A.
b. Laat met behulp van differentiëren zien dat de richtingscoëfficiënt van de


1
2
raaklijn aan f door het punt B  3,2  gelijk is aan 5.
c. Er is nog een raaklijn aan f met een richtingscoëfficiënt van 5.
Bereken exact de coördinaten van C, het raakpunt.
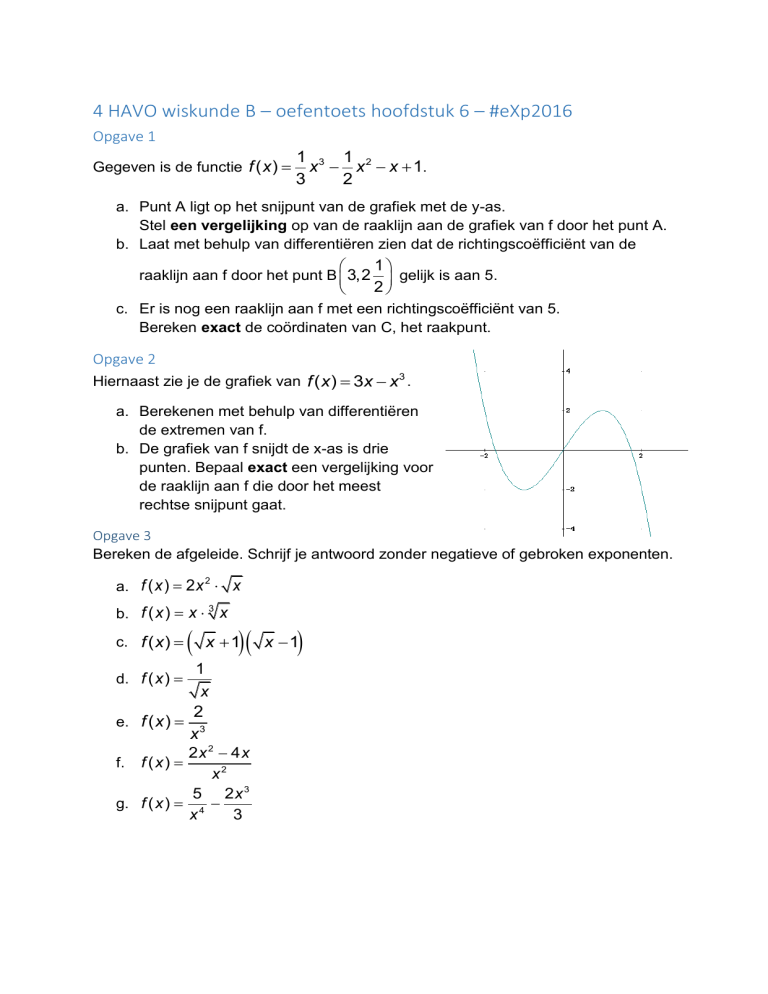
Opgave 2
Hiernaast zie je de grafiek van f ( x )  3x  x3 .
a. Berekenen met behulp van differentiëren
de extremen van f.
b. De grafiek van f snijdt de x-as is drie
punten. Bepaal exact een vergelijking voor
de raaklijn aan f die door het meest
rechtse snijpunt gaat.
Opgave 3
Bereken de afgeleide. Schrijf je antwoord zonder negatieve of gebroken exponenten.
2
a. f ( x )  2 x  x
b. f ( x )  x  3 x
c. f ( x ) 


x 1
1
x
2
e. f ( x )  3
x
2x 2  4 x
f. f ( x ) 
x2
5 2x 3
g. f ( x )  4 
x
3
d. f ( x ) 

x 1
Opgave 4
Bereken de afgeleide:
a. f ( x )  (4 x  3)8
b. g ( x )  2x  3
c. h( x ) 
1
(5 x  1)6
Opgave 5
Gegeven f ( x )   4 x  1 .
5

Bereken met behulp differentiëren in welke punten van de grafiek de raaklijn
aan f evenwijdig is aan de lijn k met als vergelijking y=20x+9?
Opgave 6
Ik wil de maximale oppervlakte van een rechthoekig veld dat met een schutting van
80 m omheind kan worden, als gebruik wordt gemaakt van een muur die aan de
overige zijde staat. Deze muur mag zo lang als nodig.

Bereken met behulp van differentiëren de maximale oppervlakte.
Opgave 7
Je krijgt 20 m draad ter beschikking. Met deze draad, dien je een rechthoek en een
vierkant te vormen. Deze figuren staan los van elkaar. De basis van de rechthoek
vormt het dubbele van een zijde van het vierkant.

Bereken met behulp van differentiëren hoeveel draad je voor elke figuur moet
gebruiken zodat de totale oppervlakte maximaal is.
EINDE