H - Wisnet

Gemeenschappelijke Propedeuse Engineering
H. 10
WISKUNDE
H.10
Goniometrie
10.1 Basisbegrippen
Regelmatig voeren we berekeningen uit, waarin één of meerdere hoeken
voorkomen.
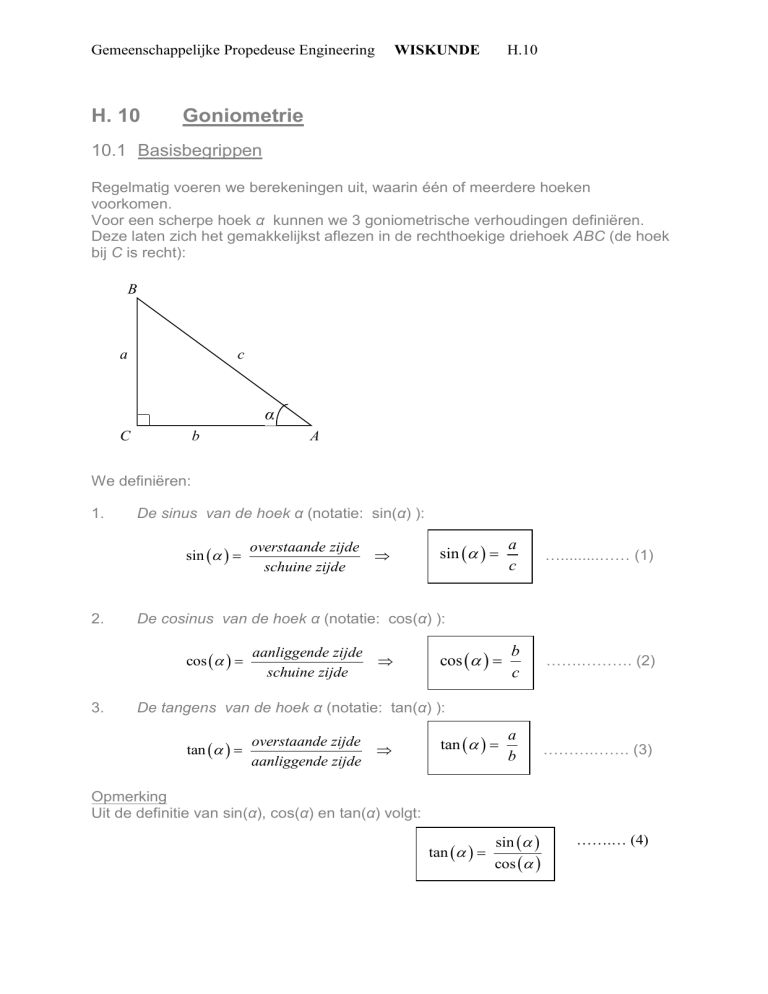
Voor een scherpe hoek α kunnen we 3 goniometrische verhoudingen definiëren.
Deze laten zich het gemakkelijkst aflezen in de rechthoekige driehoek ABC (de hoek
bij C is recht):
B
a
c
ααααα
α
C
b
A
We definiëren:
1.
De sinus van de hoek α (notatie: sin(α) ):
sin   
2.
sin   
a
c
….........…… (1)
b
c
…….………. (2)
a
b
……….……. (3)
De cosinus van de hoek α (notatie: cos(α) ):
cos   
3.
overstaande zijde

schuine zijde
aanliggende zijde

schuine zijde
cos   
De tangens van de hoek α (notatie: tan(α) ):
tan   
overstaande zijde

aanliggende zijde
tan   
Opmerking
Uit de definitie van sin(α), cos(α) en tan(α) volgt:
tan   
sin  
cos  
…….… (4)
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Voor elke rechthoekige driehoek geldt de stelling van Pythagoras:
……….……… (5)
a2  b2  c2
Voorbeeld 1a:
Bepaal in onderstaande figuur de lengte van de schuine zijde c.
Bepaal daarna voor hoek α de sinus, de cosinus en de tangens.
Oplossing:
Pythagoras: 3 2  4 2  c 2
 9  16  c 2
 25  c 2
 c5
sin   
3
5
cos   
4
5
c
3
α
tan   
4
3
4
Voorbeeld 1b:
Bepaal in onderstaande figuur de lengte van de rechthoekszijde b.
Bepaal daarna voor hoek  de sinus, de cosinus en de tangens.
5

13
b
Een hoek drukken we uit in graden. Zo komt een rechte hoek overeen met 90.
Als de grootte van een hoek bekend is, dan kan de sinus-waarde, de cosinus-waarde
en de tangens-waarde van die hoek met de rekenmachine worden bepaald.
Voorbeeld 2a:
Ga uit van een hoek α van 40, dus: α = 40
Dan kunnen we met de rekenmachine berekenen:
sin    sin  40   0.643
cos    cos  40
tan    tan  40
  0.766
  0.834
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Voorbeeld 3a:
In onderstaande rechthoekige driehoek is zijde a = 4 en hoek α = 35
Bereken de zijden b en c. Bereken ook de hoek .

c
a=4
α
Oplossing:
b
sin  35
  4c
 0.5736 
4
4
 c
 6.974
c
0.5736
tan  35
  b4
 0.7002 
4
4
 b
 5.713
b
0.7002
Voor elke driehoek geldt: de som van de hoeken is 180
Dus:     90  180  35    90  180    125  180
   55
Voorbeeld 3b:
In bovenstaande rechthoekige driehoek is zijde a = 8 en hoek  = 25
Bereken de zijden b en c. Bereken ook de hoek .
Voorbeeld 4a:
Een balk is onder een bepaalde hoek  ingeklemd in de grond. Aan het uiteinde van
de balk hangt een gewicht, welke met een verticale kracht F van 250 newton aan die
balk trekt (zie onderstaande figuur). Deze kracht F maakt een hoek van 50 met de
balk. De kracht F kunnen we ontbinden in 2 componenten:
een kracht F X , welke langs de balk valt, en een kracht F Y , welke loodrecht op de
balk staat.
Bereken de grootte van deze componenten. Bereken ook de grootte van de hoek .
FX
50
FY

F
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Oplossing:
cos  50
  FF
 0.6428 
FX
F
sin  50
  FF
 0.7660 
FY
F
X
Y
50    90  180
 FX  F  0.6428  250  0.6428  160.7 newton
 FY  F  0.7660  250  0.7660  191.5 newton
   140  180
   40
Voorbeeld 4b:
Een voorwerp wordt met een snelheid v van 12 m/s weggeschoten onder een hoek
van 65 (zie onderstaande figuur). Deze snelheid kunnen we ontbinden in 2
componenten:
Een horizontale snelheid v x en een verticale snelheid v y.
Bereken de grootte van deze componenten.
v
V
vy
65
vx
10.2 Goniometrie en de rekenmachine
We beschouwen de uitdrukking y  sin  20 .
We kunnen de waarde van y berekenen met de rekenmachine m.b.v. de sin-knop
(rekenmachine instellen op graden!): y = 0.34202
Bij deze vraag is de hoek bekend, en moet de onbekende sinus-waarde worden
berekend.
Beschouw nu de uitdrukking sin    0.62518
We kunnen de waarde van de hoek  berekenen met de rekenmachine m.b.v. de
sin-1-knop.
Als we de rekenmachine instellen op graden, dan vinden we de hoek  = 38.7
Bij deze vraag is de sinus-waarde bekend, en moet de onbekende hoek worden
berekend.
Deze laatste vraag is het omgekeerde probleem (of inverse probleem) van de eerste
vraag.
Het bepalen van de onbekende hoek  uit de vergelijking sin    0.62518 gebeurt
dus met de sin-1-knop van de rekenmachine.
Als je dit wilt opschrijven, dan kun je dit als volgt noteren:
  = sin-1 (0.62518) = 38.7
sin    0.62518
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
Voorbeeld 1:
Bepaal de grootte van de hoek in graden van:
a.
b.
sin    0.2718
cos     0.6782
d.
c.
H.10
tan    3.518
sin    0.5934
cos     0.5934
Merk op, dat hier nu geldt:     90
Voorbeeld 2a:
In onderstaande rechthoekige driehoek is zijde a = 3 en zijde c = 7
Bereken de hoek  en de zijde b.

c
a
α
b
Oplossing:
a
3
sin   
 sin     0.4286    sin 1  0.4286   25.4
c
7
cos   
b
c
 cos  25.4
  b7
 0.9033 
b
 b  7  0.9033  6.32
7
Voorbeeld 2b:
In bovenstaande rechthoekige driehoek is zijde a = 4 en zijde c = 11
Bereken de hoek  en de zijde b.
Gemeenschappelijke Propedeuse Engineering
10.3
WISKUNDE
H.10
Eenheden voor een hoek
Een hoek kun je aangeven in graden, bijvoorbeeld α = 35. De eenheid graden
behoort niet tot het SI-stelsel. Een andere eenheid voor de hoek is de radiaal,
afgekort met rad. Bijvoorbeeld  = 0.48 rad.
Deze eenheid behoort wel tot het SI-stelsel.
Het begrip radiaal hangt samen met het begrip middelpuntshoek.
Definitie:
Een middelpuntshoek is een hoek waarvan het hoekpunt in het middelpunt M van
een cirkel ligt.
In nevenstaande figuur is hoek α zo’n
middelpuntshoek.
De cirkelboog AB wordt de booglengte
genoemd.
B

A
M
Definitie radiaal:
Een middelpuntshoek α heeft de grootte van 1 radiaal, als de bijbehorende
booglengte even lang is als de straal R van de cirkel.
B
In nevenstaande figuur is de
booglengte AB even lang als
de straal R van de cirkel.
Dus: hoek α = 1 rad
R
M
α
R
A
Het verband tussen graden en radialen:
Bij een volledige rondgang langs een cirkel behoort een draaiingshoek van 360. De
middelpuntshoek α is dus 360. De bijbehorende booglengte komt dan overeen met
de omtrek 2R van de cirkel. De middelpuntshoek α komt dus ook overeen met 2
radialen.
Zodat:
360
180
2  radialen  360  1 radiaal 
graden 
1 radiaal 
graden
2

Hieruit kunnen we berekenen, dat: 1 radiaal  57.3 graden
Evenzo kunnen we concluderen:
1 graad 

180
radialen
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Voorbeeld 1a:
Onderstaande hoeken zijn gegeven in graden. Zet deze hoeken om in radialen:


1
  30    30 

  rad
180
6
6


1
  90    90 

  rad
180
2
2

19 
  19    19 

 0.33 rad
180 180

78 
  78    78 

 1.36 rad
180
180
Voorbeeld 1b:
Onderstaande hoeken zijn gegeven in graden. Zet deze hoeken om in radialen:
  60
  45
  23
  81
Voorbeeld 2a:
Onderstaande hoeken zijn gegeven in radialen. Zet deze hoeken om in graden:
1
1
180
180 
   rad     

 15
12
12

12 
1
4
1
4
   rad     
180
  0.73 rad    0.73 

180


180 
 45
4
 41.8
Voorbeeld 2b:
Onderstaande hoeken zijn gegeven in radialen. Zet deze hoeken om in graden:
1
   rad
5
1
   rad
2
  1.6 rad
Opmerking:
Als een hoek in radialen is gegeven, dan moet bij gebruik van de rekenmachine
deze staan ingesteld op radialen!!
Voorbeeld 3a:
1
1 
   rad  sin    sin     0.866
3
3 
  0.67 rad  cos     cos  0.67   0.784
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Voorbeeld 3b:
1
1 
   rad  sin    sin     0.434
7
7 
  1.09 rad  tan     tan 1.09  1.917
10.4 De grafiek van de functies sin(x) en cos(x)
Hiernaast staat de grafiek van de
functie f  x   sin  x 
Deze grafiek is getekend tussen x = 0
en
x=2
Veel golfverschijnselen zijn te
beschrijven m.b.v. een sinus-functie.
f  x   sin  x 
Als we de grafiek van de functie f  x   sin  x  tekenen tussen x = -  en x = 5 , dan
zien we:
f  x   sin  x 
We zien dat de grafiek zich steeds herhaalt.
We spreken dan van een periodieke functie. De periode ervan is 2 .
De maximale uitslag (“de amplitude”) van de golf is 1.
Hiernaast staat de grafiek van de
functie f  x   cos  x 
Deze grafiek is getekend tussen x = 0
en x = 2 . Veel golfverschijnselen
zijndus ook te beschrijven m.b.v. een
cosinus-functie.
f  x   cos  x 
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Als we de grafiek van de functie f  x   cos  x  tekenen tussen x = -  en x = 5 , dan
zien we:
f  x   cos  x 
We zien dat de grafiek zich steeds herhaalt.
Ook dit is dus een periodieke functie. De periode ervan is 2 .
De maximale uitslag (“de amplitude”) van deze golf is ook 1.