H. 10 Goniometrie

Gemeenschappelijke Propedeuse Engineering
H. 10
H.10
WISKUNDE
Goniometrie
10.1 Basisbegrippen
Regelmatig voeren we berekeningen uit, waarin één of meerdere hoeken
voorkomen.
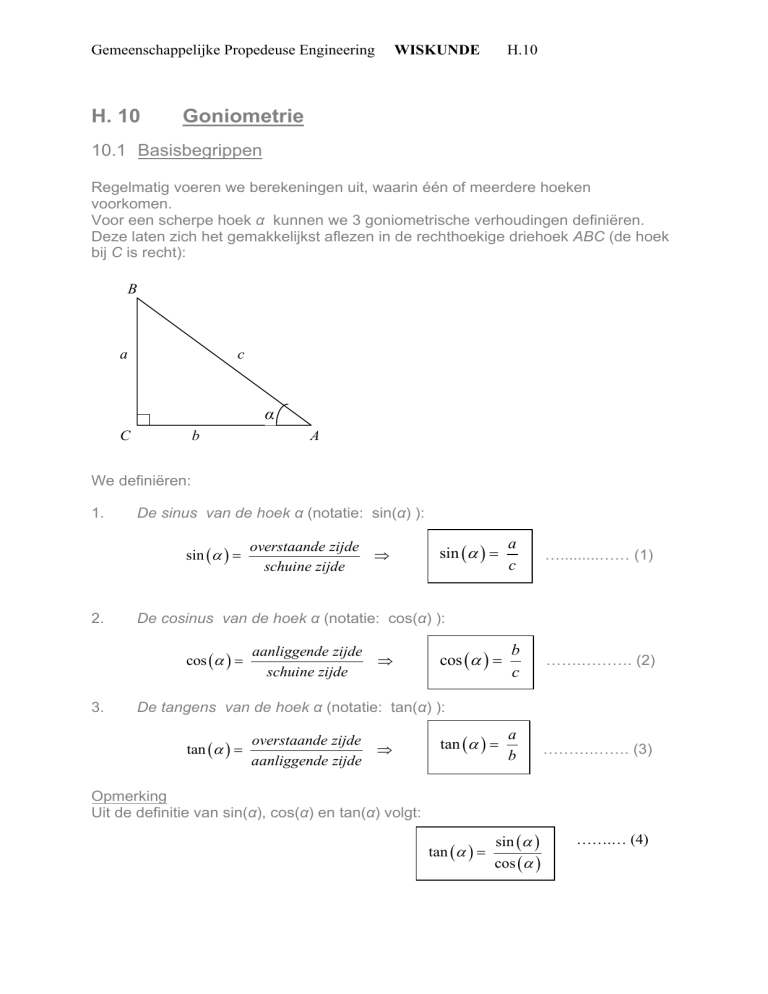
Voor een scherpe hoek α kunnen we 3 goniometrische verhoudingen definiëren.
Deze laten zich het gemakkelijkst aflezen in de rechthoekige driehoek ABC (de hoek
bij C is recht):
B
a
c
ααααα
α
C
b
A
We definiëren:
1.
De sinus van de hoek α (notatie: sin(α) ):
sin (α ) =
2.
sin (α ) =
a
c
….........…… (1)
b
c
…….………. (2)
a
b
……….……. (3)
De cosinus van de hoek α (notatie: cos(α) ):
cos (α ) =
3.
overstaande zijde
⇒
schuine zijde
aanliggende zijde
⇒
schuine zijde
cos (α ) =
De tangens van de hoek α (notatie: tan(α) ):
tan (α ) =
overstaande zijde
⇒
aanliggende zijde
tan (α ) =
Opmerking
Uit de definitie van sin(α), cos(α) en tan(α) volgt:
tan (α ) =
sin (α )
cos (α )
…….… (4)
Gemeenschappelijke Propedeuse Engineering
H.10
WISKUNDE
Voor elke rechthoekige driehoek geldt de stelling van Pythagoras:
……….……… (5)
a2 + b2 = c2
Voorbeeld 1a:
Bepaal in onderstaande figuur de lengte van de schuine zijde c.
Bepaal daarna voor hoek α de sinus, de cosinus en de tangens.
Oplossing:
Pythagoras: 3 2 + 4 2 = c 2
c
3
α
⇒ 9 + 16 = c 2
⇒ 25 = c 2
⇒ c=5
sin (α ) =
3
5
cos (α ) =
4
5
tan (α ) =
4
3
4
Voorbeeld 1b:
Bepaal in onderstaande figuur de lengte van de rechthoekszijde b.
Bepaal daarna voor hoek β de sinus, de cosinus en de tangens.
5
β
13
b
Een hoek drukken we uit in graden. Zo komt een rechte hoek overeen met 90°.
Als de grootte van een hoek bekend is, dan kan de sinus-waarde, de cosinus-waarde
en de tangens-waarde van die hoek met de rekenmachine worden bepaald.
Voorbeeld 2a:
Ga uit van een hoek α van 40°, dus: α = 40°
Dan kunnen we met de rekenmachine berekenen:
sin (α ) = sin ( 40 D ) = 0.643
cos (α ) = cos ( 40 D ) = 0.766
tan (α ) = tan ( 40 D ) = 0.834
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Voorbeeld 3a:
In onderstaande rechthoekige driehoek is zijde a = 4 en hoek α = 35°
Bereken de zijden b en c. Bereken ook de hoek β.
β
c
a=4
α
Oplossing:
b
sin ( 35 D ) =
4
4
4
⇒ 0.5736 =
⇒ c=
= 6.974
c
c
0.5736
tan ( 35 D ) =
4
4
4
⇒ 0.7002 =
⇒ b=
= 5.713
b
b
0.7002
Voor elke driehoek geldt: de som van de hoeken is 180°
Dus: α + β + 90 D = 180 D ⇒ 35 D + β + 90 D = 180 D ⇒ β + 125 D = 180 D
⇒ β = 55 D
Voorbeeld 3b:
In bovenstaande rechthoekige driehoek is zijde a = 8 en hoek β = 25°
Bereken de zijden b en c. Bereken ook de hoek α.
Voorbeeld 4a:
Een balk is onder een bepaalde hoek γ ingeklemd in de grond. Aan het uiteinde van
de balk hangt een gewicht, welke met een verticale kracht F van 250 newton aan die
balk trekt (zie onderstaande figuur). Deze kracht F maakt een hoek van 50° met de
balk. De kracht F kunnen we ontbinden in 2 componenten:
een kracht F X , welke langs de balk valt, en een kracht F Y , welke loodrecht op de
balk staat.
Bereken de grootte van deze componenten. Bereken ook de grootte van de hoek γ.
FX
50°
FY
γ
F
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Oplossing:
cos ( 50 D ) =
FX
F
⇒ 0.6428 =
FX
F
sin ( 50 D ) =
FY
F
⇒ 0.7660 =
FY
F
50 D + γ + 90 D = 180 D
⇒ FX = F ⋅ 0.6428 = 250 × 0.6428 = 160.7 newton
⇒ FY = F ⋅ 0.7660 = 250 × 0.7660 = 191.5 newton
⇒ γ + 140 D = 180 D
⇒ γ = 40 D
Voorbeeld 4b:
Een voorwerp wordt met een snelheid v van 12 m/s weggeschoten onder een hoek
van 65° (zie onderstaande figuur). Deze snelheid kunnen we ontbinden in 2
componenten:
Een horizontale snelheid v x en een verticale snelheid v y.
Bereken de grootte van deze componenten.
v
V
vy
65°
vx
10.2 Goniometrie en de rekenmachine
We beschouwen de uitdrukking y = sin ( 20° ) .
We kunnen de waarde van y berekenen met de rekenmachine m.b.v. de sin-knop
(rekenmachine instellen op graden!): y = 0.34202
Bij deze vraag is de hoek bekend, en moet de onbekende sinus-waarde worden
berekend.
Beschouw nu de uitdrukking sin (α ) = 0.62518
We kunnen de waarde van de hoek α berekenen met de rekenmachine m.b.v. de
sin-1-knop.
Als we de rekenmachine instellen op graden, dan vinden we de hoek α = 38.7°
Bij deze vraag is de sinus-waarde bekend, en moet de onbekende hoek worden
berekend.
Deze laatste vraag is het omgekeerde probleem (of inverse probleem) van de eerste
vraag.
Het bepalen van de onbekende hoek α uit de vergelijking sin (α ) = 0.62518 gebeurt
dus met de sin-1-knop van de rekenmachine.
Als je dit wilt opschrijven, dan kun je dit als volgt noteren:
sin (α ) = 0.62518
→ α = sin-1 (0.62518) = 38.7°
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
Voorbeeld 1:
Bepaal de grootte van de hoek in graden van:
a.
sin (α ) = 0.2718
b.
cos ( β ) = 0.6782
d.
c.
H.10
tan ( γ ) = 3.518
sin (α ) = 0.5934
cos ( β ) = 0.5934
Merk op, dat hier nu geldt: α + β = 90 D
Voorbeeld 2a:
In onderstaande rechthoekige driehoek is zijde a = 3 en zijde c = 7
Bereken de hoek α en de zijde b.
β
c
a
α
b
Oplossing:
a
3
⇒ sin (α ) = = 0.4286 ⇒ α = sin −1 ( 0.4286 ) = 25.4 D
sin (α ) =
c
7
cos (α ) =
b
b
b
⇒ cos ( 25.4 D ) =
⇒ 0.9033 =
⇒ b = 7 × 0.9033 = 6.32
7
7
c
Voorbeeld 2b:
In bovenstaande rechthoekige driehoek is zijde a = 4 en zijde c = 11
Bereken de hoek β en de zijde b.
Gemeenschappelijke Propedeuse Engineering
10.3
H.10
WISKUNDE
Eenheden voor een hoek
Een hoek kun je aangeven in graden, bijvoorbeeld α = 35°. De eenheid graden
behoort niet tot het SI-stelsel. Een andere eenheid voor de hoek is de radiaal,
afgekort met rad. Bijvoorbeeld β = 0.48 rad.
Deze eenheid behoort wel tot het SI-stelsel.
Het begrip radiaal hangt samen met het begrip middelpuntshoek.
Definitie:
Een middelpuntshoek is een hoek waarvan het hoekpunt in het middelpunt M van
een cirkel ligt.
In nevenstaande figuur is hoek α zo’n
middelpuntshoek.
De cirkelboog AB wordt de booglengte
genoemd.
B
α
A
M
Definitie radiaal:
Een middelpuntshoek α heeft de grootte van 1 radiaal, als de bijbehorende
booglengte even lang is als de straal R van de cirkel.
In nevenstaande figuur is de
booglengte AB even lang als
de straal R van de cirkel.
Dus: hoek α = 1 rad
B
R
M
α
R
A
Het verband tussen graden en radialen:
Bij een volledige rondgang langs een cirkel behoort een draaiingshoek van 360°. De
middelpuntshoek α is dus 360°. De bijbehorende booglengte komt dan overeen met
de omtrek 2πR van de cirkel. De middelpuntshoek α komt dus ook overeen met 2π
radialen.
Zodat:
360
180
graden ⇒
2 π radialen = 360 D ⇒ 1 radiaal =
1 radiaal =
graden
2π
π
Hieruit kunnen we berekenen, dat: 1 radiaal ≈ 57.3 graden
Evenzo kunnen we concluderen:
1 graad =
π
180
radialen
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Voorbeeld 1a:
Onderstaande hoeken zijn gegeven in graden. Zet deze hoeken om in radialen:
π
π
1
=
= π rad
α = 30 D ⇒ α = 30 ×
180 6 6
π
π
1
=
= π rad
β = 90 D ⇒ β = 90 ×
180
2
2
π
19 π
=
≈ 0.33 rad
α = 19 D ⇒ α = 19 ×
180 180
π
78 π
=
≈ 1.36 rad
γ = 78 D ⇒ γ = 78 ×
180
180
Voorbeeld 1b:
Onderstaande hoeken zijn gegeven in graden. Zet deze hoeken om in radialen:
α = 60 D
β = 45 D
α = 23 D
γ = 81D
Voorbeeld 2a:
Onderstaande hoeken zijn gegeven in radialen. Zet deze hoeken om in graden:
D
D
1
1
180
180 π
=
= 15 D
α = π rad ⇒ α = π ×
12
12
π
12 π
1
β = π rad
4
1
180
180 π
⇒ β = π×
=
= 45 D
4
π
4π
γ = 0.73 rad ⇒ α = 0.73 ×
D
180
π
D
D
= 41.8 D
Voorbeeld 2b:
Onderstaande hoeken zijn gegeven in radialen. Zet deze hoeken om in graden:
1
α = π rad
5
1
β = π rad
2
γ = 1.6 rad
Opmerking:
Als een hoek in radialen is gegeven, dan moet bij gebruik van de rekenmachine
deze staan ingesteld op radialen!!
Voorbeeld 3a:
1
⎛1 ⎞
α = π rad ⇒ sin (α ) = sin ⎜ π ⎟ = 0.866
3
⎝3 ⎠
β = 0.67 rad ⇒ cos ( β ) = cos ( 0.67 ) = 0.784
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Voorbeeld 3b:
1
⎛1 ⎞
α = π rad ⇒ sin (α ) = sin ⎜ π ⎟ = 0.434
7
⎝7 ⎠
β = 1.09 rad ⇒ tan ( β ) = tan (1.09 ) = 1.917
10.4 De grafiek van de functies sin(x) en cos(x)
Hiernaast staat de grafiek van de
functie f ( x ) = sin ( x )
f ( x ) = sin ( x )
Deze grafiek is getekend tussen x = 0
en
x=2π
Veel golfverschijnselen zijn te
beschrijven m.b.v. een sinus-functie.
Als we de grafiek van de functie f ( x ) = sin ( x ) tekenen tussen x = - π en x = 5 π, dan
zien we:
f ( x ) = sin ( x )
We zien dat de grafiek zich steeds herhaalt.
We spreken dan van een periodieke functie. De periode ervan is 2 π.
De maximale uitslag (“de amplitude”) van de golf is 1.
Hiernaast staat de grafiek van de
functie f ( x ) = cos ( x )
Deze grafiek is getekend tussen x = 0
en x = 2 π. Veel golfverschijnselen
zijndus ook te beschrijven m.b.v. een
cosinus-functie.
f ( x ) = cos ( x )
Gemeenschappelijke Propedeuse Engineering
WISKUNDE
H.10
Als we de grafiek van de functie f ( x ) = cos ( x ) tekenen tussen x = - π en x = 5 π, dan
zien we:
f ( x ) = cos ( x )
We zien dat de grafiek zich steeds herhaalt.
Ook dit is dus een periodieke functie. De periode ervan is 2 π.
De maximale uitslag (“de amplitude”) van deze golf is ook 1.