Raf: 0032-486287070

H11. Goniometrie.
§11.1 Functie voor sinus.
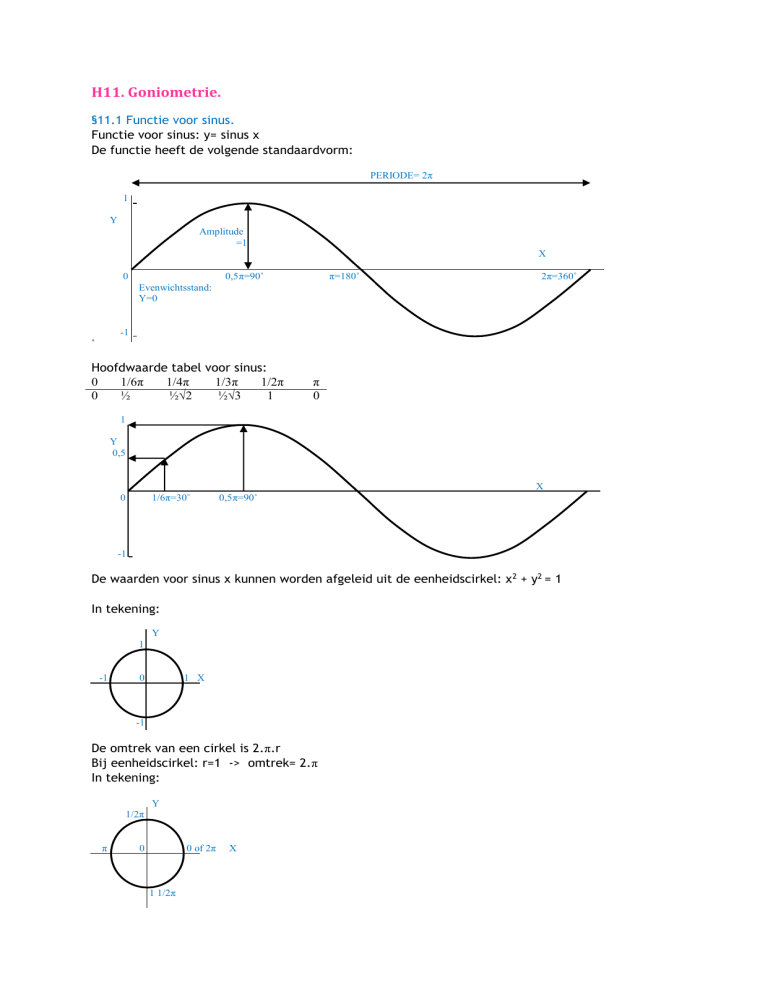
Functie voor sinus: y= sinus x
De functie heeft de volgende standaardvorm:
PERIODE= 2π
1
Y
Amplitude
=1
X
0
π=180˚
0,5π=90˚
2π=360˚
Evenwichtsstand:
Y=0
-1
˚
Hoofdwaarde tabel voor sinus:
0
1/6π
1/4π
1/3π
1/2π
0
½
½√2
½√3
1
π
0
1
Y
0,5
X
0
1/6π=30˚
0,5π=90˚
-1
De waarden voor sinus x kunnen worden afgeleid uit de eenheidscirkel: x2 + y2 = 1
In tekening:
Y
1
-1
0
1 X
-1
De omtrek van een cirkel is 2.π.r
Bij eenheidscirkel: r=1 -> omtrek= 2.π
In tekening:
Y
1/2π
π
0
0 of 2π
1 1/2π
X
De sinus is de verticale beweging (↑) vanuit het midden van de cirkel O.
sinus 45˚= ½ √2
B
45˚
½√2
O
Als je vanuit het midden van de eenheidscirkel O in een hoek van 45˚
naar de eenheidscirkel beweegt, snijd je de cirkel in punt B.
Punt B ligt ½ √2 cm hoger dan punt O: sinus 45˚= ½ √2
Elke π-waarde op de cirkel correspondeert met een hoek vanuit het midden van de cirkel:
Als je vanuit punt A langs de cirkel loopt, kom je uit bij punt B na een afstand van ¼π = 0,79 cm.
sinus (¼π)= sinus 45˚= ½ √2
B
¼ π= 0,79cm
45˚
½√2
O
A
sinus (¼ π)= ½ √2 met Radian
sinus 45˚= ½ √2 met Degree
Van graden naar radialen en omgekeerd: 2π=360˚ en π=180˚
Voorbeeld 1.
a. Bereken sinus 150˚
b. Zet om in radialen.
c. Zet a. en b. in een tekening.
d. Leg uit in woorden.
Antwoord.
a. sinus 150˚= 0,5
b. sinus (150/180) . π= sinus (5/6 . π)= 0,5
c.
5/6 . π= 2,62 cm.
B
0,5cm
150˚
O
1cm
A
d. Als je vanuit het midden van de eenheidscirkel O in een hoek van 150˚
naar de eenheidscirkel beweegt, snijd je de cirkel in punt B.
Punt B ligt 0,5cm hoger dan punt O: sinus 150˚= 0,5
Als je vanuit punt A langs de cirkel loopt,
kom je uit bij punt B na afstand van 5/6 π= 2,62 cm.
§11.2 Functie voor cosinus.
Functie voor cosinus: y= cos x
De functie heeft de volgende standaardvorm:
1
0
1/2π=90˚
π =180˚
1,5π=270˚
2π=360˚
-1
Hoofdwaarde tabel voor cosinus
0
1/6π
1/4π
1/3π
1/2π
1
½.√3
½√2
½
0
π
-1
De cosinus is de horizontale beweging (→) vanuit het midden van de cirkel.
Elke π-waarde op de cirkel correspondeert met een hoek vanuit het midden van de cirkel:
sinus(1/3π)= sinus 60˚= ½
B
1/3π= 1,05cm.
O
60˚
½
A
Als je vanuit het midden van de eenheidscirkel O in een hoek van 60˚
naar de eenheidscirkel beweegt, snijd je de cirkel in punt B.
Punt B ligt een ½cm rechts van punt O: sinus 60˚= ½
Als je vanuit punt A langs de cirkel loopt, kom je uit bij punt B
na een afstand van 1/3π= 1,05cm: sinus(1/3π)= ½
Voorbeeld 2.
a. Bereken cosinus 180˚
b. Zet om in radialen.
c. Zet a. en b. in een tekening.
d. Leg uit in woorden.
Antwoord.
a. cosinus 180˚= -1
b. cosinus (180/180) . π= cosinus ( π)= -1
c.
π= 3,14 cm.
B
-1
180˚
O
A
d. Als je vanuit het midden van de
eenheidscirkel O in een hoek van 180˚
naar de eenheidscirkel beweegt,
snijd je de cirkel in punt B.
Punt B ligt 1cm links van punt O:
cosinus 180˚= -1
Als je vanuit punt A langs de cirkel loopt,
kom je uit bij punt B na een afstand
van π= 1,57cm.
§11.3 Rekenregels bij sinus.
2 goede oplossingen per periode.
Bij sinus:
spiegelen met half π: a=goed en dus ook a’, bijv. 1/4 π en dus ook 3/4 π
of met anderhalf π: b=goed en dus ook b’, bijv. 1,1π en dus ook 1,9π
1
b
1,5π
b’
0
a
0,5π
a’
-1
Bij cosinus:
spiegelen met π: a=goed en dus ook a’, bijv. 1/2 π en dus ook 1 1/2 π
1
0
a
π
a’
-1
NB: Periode niet altijd gelijk aan 2π
Periode formule: 2 goede oplossingen per elke volgende periode.
sin t= sin(t+2π)= sin(t+2kπ) met k= hele getallen
cos t= cos(t+2π)= cos(t+2kπ)
1
0
-1
NB: Periode niet altijd gelijk aan 2π
Voorbeeld 3.
sin(x)= ½
a. Geef 4 goede oplossingen.
b. Zet de 4 oplossingen in een tekening.
c. Zet 2 goede oplossingen in de eenheidscirkel.
Antwoord.
a. sin-1(0,5)= 0,5235: 1/6π, 5/6π, 2 1/6π, 2 5/6π.
b.
1
0
1/6π
5/6π
2 1/6π
2 5/6π
-1
c.
sinus 1/6π= ½ (zie tekening A)
Er is een ander punt dat ook een verticale beweging heeft van ½ (Zie tekening B).
Tekening A:
Tekening B:
5/6 π
B
1/6 π=
½
½
½
A
A
Voorbeeld 4.
cos(x)= ½
a. Geef 4 goede oplossingen.
b. Zet de 4 oplossingen in een tekening.
c. Zet 2 goede oplossingen in de eenheidscirkel.
Antwoord.
a. 1/3π, 1 2/3π, 2 1/3π, 3 2/3π.
b.
1
0
1/3π
1 2/3π
2π
2 1/3π
3 2/3π
-1
c.
cosinus 1/3π= ½ (zie tekening A)
Er is een ander punt dat ook een horizontale beweging heeft van ½ (zie tekening B).
Tekening A:
Tekening B:
B
1/2
1/3π
0
A
0
A
1 2/3π
Voorbeeld 5.
sin(2x)= ½
a. Geef alle goede oplossingen.
b. Zet de oplossingen in een tekening voor Domein [0, 4 π].
Antwoord.
sin(1/6π)= ½ en sin(5/6π)= ½
2x= 1/6π + 2kπ en 2x= 5/6π + 2kπ ->
x= 1/12π + kπ en x= 5/12π + kπ
Merk op: Periode is nu 1π
b.
1/4π
1
0,5
0
1/12π 5/12π
π
2π
3π
4π
-1
3/4π
Voorbeeld 6.
sin(½x)= ½
a. Geef alle goede oplossingen.
b. Zet de oplossingen in een tekening voor Domein [0, 4π].
Antwoord.
½x= 1/6π + 2kπ en ½x= 5/6π + 2kπ ->
x= 1/3 π + 4kπ en x= 1 2/3π + 4kπ
Merk op: Periode is nu 4π
b.
1
π
0,5
2π
0
1/3π
2
4
1 2/3π 6
4π
8
10
-1
3π
kwadratenformule
sin2t + cos2t= 1
1
½√2
0
-1
Bij snijpunten y:
02 + 12= 1
Bij snijpunten functies: ( ½√2 )2 + ( ½√2 )2= 1
Ook geldt sin2(at+b) + cos2(at+b)= 1
Verdubbelingsformules.
sin(2t)= 2. cos t . sin t
cos(2t)= cos2t – sin2t
cos(2t)= 2cos2t – 1
cos(2t)= 1 – 2 . sin2t
12
§11.4 Afgeleide en integralen.
Afgeleiden:
y= sin x ->
y´= cos x
1
y= sin x
0
-1
MAX.
1 stijging
y'= cos x
Δ=0
0
Δ=0
-1
MAX daling
y= cos x ->
y´= -sin x
1
y= cos x
0
-1
1
MAX stijging
y= -sin x
Δ=0
0
Δ=0
-1
MAX daling
Integralen:
y= sin x ->
F= -cos x + c
y= cos x ->
F= sin x + c
§11.5 Sinus en cosinus in een rechthoekige driehoek.
We hebben gezien dat in een eenheidscirkel de cosinus de verandering geeft
langs de x-as en de sinus de verandering langs de y-as
In tekening:
sin x
cos x
Je kan de driehoek uit de tekening halen en dan gelden de volgende regels:
c
b
α
a
cos α= a/c
sin α= b/c
tan α= b/a
NB: In eenheidscirkel r(=c)=1 >
cos α= a
sin α= b
Voorbeeld 7.
Een man staat 30 meter voor een toren.
De hoek van de man met de toren is 60˚.
Hoe hoog is de toren.
Antwoord.
Data in een tekening:
c
☺
cos 60˚= 0,5
30/c= 0,5 -> c= 60
Check:
tan 60˚= 1,73
51,96/30= 1,73
b
60˚
30 meter
sin 60˚= 0,866
b/60= 0,866 -> b= 51,96
§11.6 De eenheidscirkel als relatie.
We hebben gezien dat de waarden voor de sinus en de cosinus kunnen worden
afgeleid uit de eenheidscirkel: x2 + y2= 1.
De eenheidscirkel kan worden geschreven als functie van de cosinus en sinus.
De cosinus is de horizontale beweging en geeft de waarde op de x-as.
De sinus is de verticale beweging en geeft de waarde op de y-as.
In tekening:
Y
1
-1
1/2π
0
1 X
π
B
0
(x,y)= (cos1/2π,sin1/2π)= (0,1)
A
(x,y)= cos 0, sin 0)= (1,0)
1 1/2π
-1
x= cos t
y= sin t
Voor t=0:
x= cos 0= 1
y= sin 0= 0
Punt A is (x,y)= (0,1)
Voor t=1/2 π:
x= cos(1/2 π)= 0
y= sin(1/2 π)= 1
Punt B is (x,y)= (1,0)
In wiskundige vergelijking:
x= cos t
y= sin t
x2= cos2 t
y2= sin2 t
x2= cos2 t
y2= sin2 t +
x2 + y2= 1
NB: cos2 t + sin2 t= 1
x2 + y2= 1 ->
y2= 1 - x2 ->
y= +√(1 - x2) en -√(1 - x2)
NB: Dit is de vergelijking voor de eenheidsfunctie.
Y
1
y= +√(1 - x2)
-1
0
1 X
y= -√(1 - x2)
-1
We zullen straks zien dat je elke cirkel en ellips op een vergelijkbare manier
kan bekijken zoals we nu net gedaan hebben.
§11.7 Vergelijking voor een ellips.
De vergelijking voor een ellips:
x(t)= a + r1 . cos t
y(t)= b + r2 . sin t
(a,b)= midden van de ellips
r1: 2r1 is de lengteas (→) van de ellips
r2: 2r2 is de breedteas (↑) van de ellips
met a, b, r1 en r2 kan je de ellips tekenen
Voorbeeld 8.
x(t)= 2 + 2 . cos t
y(t)= 3 + 3 . sin t
Teken de ellips.
Antwoord.
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
§11.8 Herschrijven van cirkel en ellips tot een vergelijking.
Je kan een cirkel en een ellips herschrijven tot een vergelijking.
Voorbeeld 9.
x(t)= 2 + 2 . cos t
y(t)= 2 + 2 . sin t
a. Maak een tekening.
b. Herschrijf tot vergelijking.
Antwoord.
a.
4
3
2
1
0
1
2
3
4
5
6
b.
(x-2)2= 4 . cos2t
(y-2)2= 4 . sin2t +
(x-2)2 + ( y-2)2= 4
(y-2)2= 4 - (x-2)2 ->
y-2 = -√4 - (x-2)2 en +√4 - ( x-2 )2 ->
y= -√4 - (x-2)2 + 2 en +√4 - (x-2)2 + 2
4
y= +√4 - (x-2)2 + 2
3
2
y= -√4 - (x-2)2 + 2
1
0
1
2
3
4
5
6
§11.8 Richting, snelheid en afstand in cirkel en ellips.
De richting in een cirkel: y´/x´
De afstand tot de oorsprong: √(x2 + y2 )
De maximale afstand tot de oorsprong: (x2 + y2 )’=0
Hoogste of laagste punt: y’= 0
Meest linkse of meest rechtse punt: x’= 0
De snelheid op een cirkel= √(x´2 + y´2 )
Voorbeeld 10.
x(t)= 2 + 2 . cos t
y(t)= 2 + 2 . sin t
Bereken richting, maximale afstand tot de oorsprong en snelheid.
Antwoord.
Richting
x´= -2 . sin t
y´= 2 . cos t
y´/x´= -cos t/ sin t
Afstand.
x2= 4 + 4 . cos2t + 4 . cos t
y2= 4 + 4 . sin2t + 4 . sin t
x2+y2= 4 + 4 . cos2t + 4 . cos t + 4 + 4 . sin2t + 4 . sin t ->
4 + 4 . (cos2t + sin2t ) + 4 . cos t + 4 + 4 . sin t ->
12 + 4 . cos t + 4 . sin t
Maximale afstand.
Maximum bij (x2+y2 )´=( 12 + 4 . cos t + 4 . sin t )’= 4 . sin t – 4 . cos t ->
Maximum bij: 4 . sin t = 4 . cos t -> t= 1/4π
Afstand tot oorsprong= √(x2 + y2 )= √(12 + 4 . cos t + 4 . sin t )=
√(12 + 4 . cos (1/4π ) + 4 . sin (1/4 π )= √23,31= 4,83 (zie tekening).
Hoogste en laagste punt bij y’=0: 2 . cos t=0 -> t= 1/2π en t= 1½π
Meest linkse of meest rechtse punt bij x’=0: -2 . sin t=0 -> t= 0 en t= π (zie tekening).
Snelheid.
x´= -2 . sin t en y´= 2 . cos t
√(x´2 + y´2)= (4 . sin2t + 4 . cos2y )= √4= 2
6
5
t=½π
4
t=¼π
3
4,83
2 t=π
t=0
1
t=1½π
0
1
2
3
4
5
6
§11.9 Oppervlakte in een cirkel en ellips.
Methode 1:
Oppervlakte in een cirkel: π . r2
Oppervlakte in een ellips: π . r1 . r2
Methode 2:
Functie bepalen en oppervlakte berekenen met GR.
Voorbeeld 11.
x(t)= 2 . cos t
y(t)= 3 . sin t
Bepaal het oppervlakte boven de x-as.
Antwoord.
3
2
1
-2
-1
0
1
2
-1
-2
-3
Methode 1:
Oppervlakte ellips= 2.3. π= 6. π
Halve ellips= 3. π= 9,42
Methode 2:
x2= 4 . cos2 t
y2= 9 . sin2 t
2,25 x2
= 9 . cos2 t
y2
= 9 . sin2 t +
2
2
2,25 x + y = 9 ->
y2= 9 – 2,25x2 ->
y= +√ (9 – 2,25 x2 ) en -√ (9 – 2,25 x2 )
Grafisch:
Math 9:fnInt(
functie, x, ondergrens, bovengrens) ->
√(9 – 2.25 x2), x, -2, 2)= 9,42
§11.10 Harmonische cirkelbeweging.
Een mannetje staat op de rotonde in punt A.
Je projecteert het mannetje loodrecht op een as onder de rotonde.
Je meet de afstand van het mannetje tot punt S op de x-as.
Je kan vrij eenvoudig inzien dat de afstand van het mannetje
tot startpunt S zich ontwikkelt als een sinus.
Bij A loopt het mannetje bijna parallel aan de as naar rechts.
De afstand tot S stijgt dan bijna maximaal.
Vlakbij B bereikt het mannetje de maximale afstand tot S.
Het mannetje loopt bijna haaks op de x-as en de afstand tot S stijgt bijna niet meer.
Van B naar C loopt het mannetje weer terug naar de beginwaarde S.
Van C naar A kan je op een vergelijkbare manier omschrijven.
C
D
B
A
☺
-2
S=0
2
2
0
A=S
-2
B
C=S
D
A
De formule om de afstand te berekenen van het mannetje
tot het punt x=0 ziet er zo uit:
2π
x(t)= b + a . sin [
. ( t-d ) ]
T
a
☺
d
t=0
x=0
b
Als je wil weten waar het mannetje is op de x-as kan je logisch beredeneren dat
dit afhangt van de ligging van de rotonde, de startpositie van de man op de rotonde,
de grootte van de rotonde, hoe snel hij loopt en hoe lang hij heeft gelopen.
Dat zijn precies de kengetallen die je terugziet in de formule.
b= startpositie op rotonde voor t=0
Als mannetje begint op startpositie: d=0
d= tijd die het mannetje nodig heeft om bij de startpositie aan te komen,
als hij loopt in de goede richting (tegen klok in).
a=straal van de rotonde (=grootte van de rotonde)
t= hoelang hij loopt
T= omloopperiode (=1x rotonde rond)
Voorbeeld 12.
Het volgende plaatje is gegeven:
☺Q
t=0
☺P
x=0
2 mannetjes P en Q staan op een rotonde.
De tijd die ze nodig hebben om de rotonde rond te lopen is 4 seconden.
Maak voor beide mannetjes een vergelijking om hun afstand tot x=0 te berekenen.
Antwoord.
2π
x(t)= b + a . sin [
. ( t-d) ]
T
voor P:
x(t)= 4 + 2 . sin (0,5π . t)
voor Q:
x(t)= 4 + 2 . sin [0,5π . ( t-1)]
Q loopt kwart rotonde achter= 1 seconde
-11.10.1 De Hoeksnelheid.
Hoeksnelheid ω= 2 π/T
Voorbeeld 13.
Omloopperiode T= 4 seconden.
a. Wat betekent T=4.
b. Wat is de hoeksnelheid.
c. Wat betekent dit.
d. Weet je nu ook de snelheid en de afgelegde afstand.
Antwoord.
a. Het mannetje loopt de rotonde rond in 4 seconden.
b. 2π/4= 0,5π
c. Je loopt in 1 seconde een kwart rotonde.
d. Nee, dat hangt af van de grootte van de rotonde.
§11.11 Vergelijking voor een cirkel.
De vorige formule was om een projectie op de x-as te berekenen.
Met de volgende formule kan je precies de plaats van het mannetje
op de rotonde bepalen:
Als je wil weten waar het mannetje is op de rotonde is,
kan je logisch beredeneren dat dit afhangt van de ligging van de rotonde,
de startpositie van de man op de rotonde,
de grootte van de rotonde, hoe snel hij loopt en hoe lang hij heeft gelopen.
Dat zijn precies de kengetallen die je terugziet in de formule.
2π
x(t)= a + r . cos [
. (t-d) ]
T
2π
y(t)= b + r . sin [
. (t-d) ]
T
(a,b)
r
Startpositie:
(a+r,b)
d
(a,b)= midden van de rotonde
r= straal van de rotonde
met a, b en r kan je de rotonde tekenen
Startpositie van de rotonde bij (a+r,b)
Als mannetje begint op startpositie: d=0
d= tijd die het mannetje nodig heeft om bij de startpositie aan te komen,
als hij loopt in de goede richting (tegen klok in).
t= hoelang hij loopt
T= de omloopperiode
Voorbeeld 14.
Het volgende plaatje is gegeven:
(2,2)
2
Startpositie:
t=0
☺=P
☺=Q
2 mannetjes P en Q staan op een rotonde.
De tijd die ze nodig hebben om de rotonde rond te lopen is 2 π seconden.
Maak voor beide mannetjes een vergelijking om hun plaats
op de rotonde te berekenen.
Antwoord.
2π
x(t)= a + r . cos [
. (t-d ) ]
T
2π
y(t)= b + r . sin [
. (t-d ) ]
T
Voor P:
x(t)= 2 + 2 . cos t
y(t)= 2 + 2 . sin t
Voor Q:
x(t)= 2 + 2 . cos (t - 0,5π)
y(t)= 2 + 2 . sin (t - 0,5π)
§11.12 Transformatie van sinusfuncties.
§11.12.1 Een functie naar rechts schuiven.
Je kan een functie naar rechts schuiven.
Algemene vorm: y= f(x) -> f(x–c1)
Als je c1 naar rechts wil:
y= sin x ->
y= sin (x–c1)
Voorbeeld 15.
y= sin x
Verschuif de functie π naar rechts.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= sin (x- π)
1
Y
0
X
π
-1
§11.12.2 Een functie omhoog schuiven.
Je kan een functie omhoog schuiven.
Algemene vorm: y= f(x) -> f(x) + c2
Als je c2 omhoog wil:
y= sin x ->
y= sin x + c2
Voorbeeld 16.
y= sin x ->
Verschuif de functie 1 naar omhoog.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= sin x + 1
1
Y
0
-1
X
§11.12.3 Een functie met een factor vergroten.
Je kan alle y-waarden met een factor c3 vergroten.
Algemene vorm: y= f(x) -> y= c3 . f(x)
y= sin x ->
y= c3 . (sin x)
= amplitude verandert met factor c3.
Voorbeeld 17.
y= sin x ->
Vergroot alle y-waarden met een factor 2.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= 2 . (sin x)
1
Y
0
X
-1
§11.12.4 De afstand tot de y-as met een factor vergroten.
Je kan voor elke y-waarde de afstand tot de y-as met een factor c4 vergroten.
Algemene vorm: y= f(x) -> y= f (1/c4 . x)
y= sin x ->
y= sin (1/c4 . x)
NB:
Je vergroot de periode met factor c4.
sin (2x)= sin (1:½ . x) -> Periode wordt half zo groot (c4=1/2).
sin (½x)= sin (1:2 . x) -> Periode wordt 2x zo groot (c4=2).
NB: 1:½ = 2
Voorbeeld 18.
y= sin x
Halveer de afstand van de y-waarden tot de y-as met een factor 2.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= sin(2 . x)
1
Y
0
-1
X
§11.12.5 De functie spiegelen in de y-as.
Als c4= -1: alle y-waarden worden gespiegeld in de y-as.
Algemene vorm: y= f(x) -> y= f(-x)
y= sin x ->
y= sin (-x)
Voorbeeld 19.
y= sin x
Spiegel alle y-waarden in de y-as.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= sin(-x)
Y 1
X
0
-1
Voorbeeld 20.
Y
1
X
0
π
2π
Geef de vergelijking voor de bovenstaande functie.
Antwoord.
y= 2 . sin (½ (x – π) ) + 1
3π
4π
5π
§11.13 Een schommeling rond een trend.
Een trendlijn is een stijgende of dalende lijn
die de lange termijnontwikkeling weergeeft.
Een lineaire functie kan je opvatten als trend lijn.
De lineaire functie heeft de bekende vorm:
y= b + ax
Een sinus kan een schommeling rond de trend geven.
Algemene vorm:
y= d . sin (c.x)
d geeft de hoogte van de amplitude.
Met de hoogte van c kan je de periode afstellen:
c= 2π/periode
Voorbeeld 22.
Voor een periode van 8 jaar is de volgende trend voorspeld:
y= 0,5 . x + 1,5
Rond de trend is een golfbeweging van 4 jaar
met een maximale afwijking van de trend van 1.
a. Geef de functie.
b. Teken schetsmatig.
a.
Maximale amplitude is 1 -> d=1
c= 2π/4= 1,571
y= 0,5 . x + 1,5 + sin (1,571x)
b.
6
Y
y=0,5 . x + 1,5
5
y= 0,5 . x + 1,5 + sin(1,571x)
1
-1
4
3
1
-1
2
1
X
0
1
2
3
4
5
6
7
8