Exacte waarden bij sinus en cosinus

Exacte waarden bij sinus en cosinus
In enkele gevallen kun je vergelijkingen met sinus en cosinus exact
oplossen. Welke gevallen zijn dat?
y
y
1
1
f(x) = sin x
0,5
π
–π
–2
–1 O
–0,5
1
2
3
4
5
2π
6
3π x
7
8
9
–π
–1
1
a
b
c
d
e
2
a
b
c
d
g(x) = cos x
0,5
–2
–1 O
–0,5
1
2
3π
4
5
6 2π 7
9 3π
8
x
–1
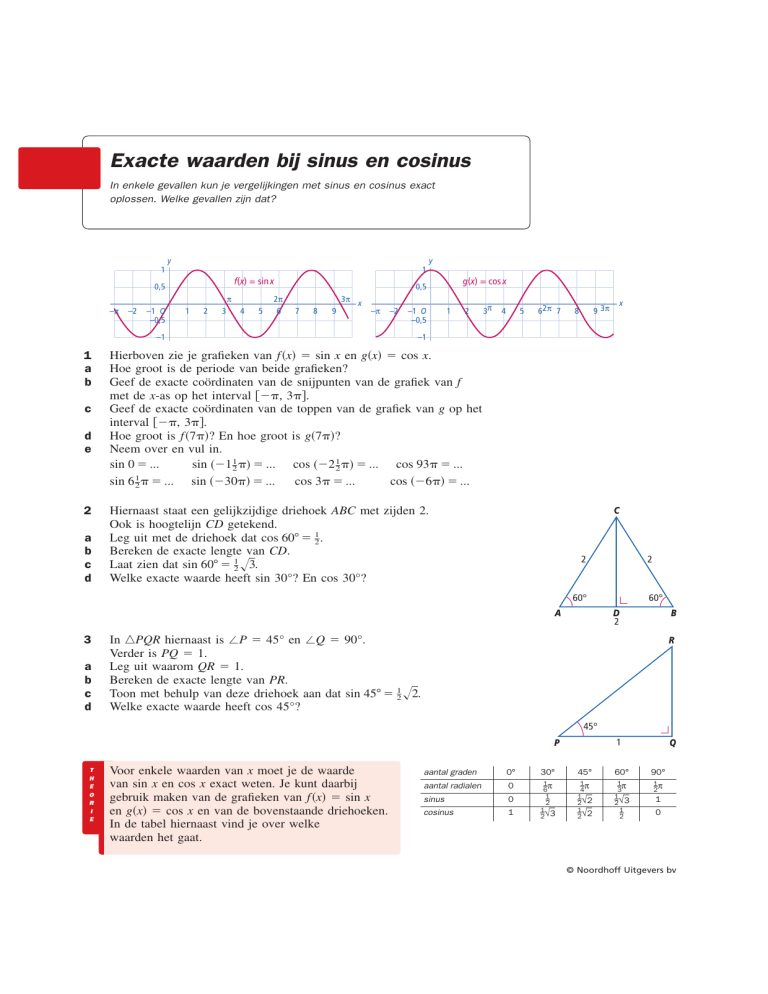
Hierboven zie je grafieken van f 共x兲 ⫽ sin x en g共x兲 ⫽ cos x.
Hoe groot is de periode van beide grafieken?
Geef de exacte coördinaten van de snijpunten van de grafiek van f
met de x-as op het interval 关⫺␲, 3␲兴.
Geef de exacte coördinaten van de toppen van de grafiek van g op het
interval 关⫺␲, 3␲兴.
Hoe groot is f 共7␲兲? En hoe groot is g共7␲兲?
Neem over en vul in.
sin 0 ⫽ ...
sin 共⫺1 21 ␲兲 ⫽ ... cos 共⫺2 21 ␲兲 ⫽ ... cos 93␲ ⫽ ...
1
sin 6 2 ␲ ⫽ ... sin 共⫺30␲兲 ⫽ ...
cos 3␲ ⫽ ...
cos 共⫺6␲兲 ⫽ ...
Hiernaast staat een gelijkzijdige driehoek ABC met zijden 2.
Ook is hoogtelijn CD getekend.
Leg uit met de driehoek dat cos 60⬚ ⫽ 21 .
Bereken de exacte lengte van CD.
Laat zien dat sin 60⬚ ⫽ 21 冪3.
Welke exacte waarde heeft sin 30°? En cos 30°?
C
2
2
60°
A
3
a
b
c
d
60°
D
2
B
In 䉭PQR hiernaast is ⬔P ⫽ 45° en ⬔Q ⫽ 90°.
Verder is PQ ⫽ 1.
Leg uit waarom QR ⫽ 1.
Bereken de exacte lengte van PR.
Toon met behulp van deze driehoek aan dat sin 45⬚ ⫽ 21 冪2.
Welke exacte waarde heeft cos 45°?
R
45°
1
P
T
H
E
O
R
I
E
Voor enkele waarden van x moet je de waarde
van sin x en cos x exact weten. Je kunt daarbij
gebruik maken van de grafieken van f共x兲 ⫽ sin x
en g共x兲 ⫽ cos x en van de bovenstaande driehoeken.
In de tabel hiernaast vind je over welke
waarden het gaat.
Q
aantal graden
0°
30°
45°
60°
90°
aantal radialen
0
1
–π
6
1
–π
3
1
–π
2
sinus
0
1
–
2
–12√3
1
cosinus
1
–12√3
1
–π
4
–12√2
–12√2
1
–
2
0
© Noordhoff Uitgevers bv
4
a
b
c
5
a
b
c
d
A
A
N
P
A
K
Gebruik de grafieken op de vorige bladzijde.
Geef van de volgende vergelijkingen de exacte
oplossingen op het interval 关⫺␲, 3␲兴.
sin x ⫽ 21
d cos x ⫽ 0
sin x ⫽ ⫺ 21
e sin x ⫽ 21 冪2
1
f cos x ⫽ ⫺ 21 冪3
cos x ⫽ 2
Hiernaast staat de grafiek van f共x兲 ⫽ cos 3x op
het interval 关⫺␲, ␲兴.
In deze opdracht ga je de vergelijking cos 3x ⫽ 21 冪3
op het interval 关⫺␲, ␲兴 oplossen.
Voor één oplossing geldt 3x ⫽ 61 ␲. Leg dat uit.
1
Eén oplossing is x ⫽ 61 ␲ ⬊ 3 ⫽ 18
␲.
Welke oplossing volgt dan uit de symmetrie in de
y-as?
Welke periode heeft de grafiek van f?
Gebruik de periode om de overige vier oplossingen
te berekenen.
sin x ⫽ ⫺1
sin x ⫽ 21 冪3
cos x ⫽ ⫺ 21 冪2
g
h
i
y
1
0,5
π
–π
–3
–2
–1
O
1
2
3
4
5
6
7
7
11
1––π
1––π
12
12
–0,5
–1
Hoe los je de vergelijking f(x) = p met f een goniometrische functie en p
een constante, exact op een gegeven interval op?
1 Gebruik de tabel met exacte waarden en zonodig de grafiek om één
oplossing te vinden.
2 Stel de periode van de functie vast.
3 Schets de grafiek van f op het gegeven interval en geef de gevonden
oplossing in de schets aan.
4 Gebruik de periode en de symmetrie van de grafiek om de overige
oplossingen te vinden.
Voorbeeld
1
Los 4 + 3sin 2x = 2–
op het interval [–π, 2π] exact op.
y
2
Oplossing
1 4 + 3sin 2x = 2–1
7
2
6
1
3sin 2x = –1–2
5
sin 2x = – –1
2
4
Met behulp van de tabel en de grafiek:
3
1
1
één oplossing is 2x = – –π
dus x = –––π.
6
12
2
1
2 De periode is 2π : 2 = π.
3 Zie de schets hiernaast.
5
1
of x = – ––π
4 De oplossingen zijn: x = –––π
12
–π
–4
12
7 of x = ––π
11 of x = 1––π
7 of x = 1––π
11
of x = ––π
12
© Noordhoff Uitgevers bv
12
12
12
–3
–2 –1 O
5
1
– ––π
– ––π
12
12
1
–π
4
π
1
2
3
7
11
––π
––π
12
12
2π
x
x
6
a
b
Los de volgende vergelijkingen op het gegeven interval exact op.
2 sin 3x ⫽ 冪3 op 关⫺␲, ␲兴
6 cos 21 x ⫽ 3冪2 op 关0, 3␲兴
7
a
b
c
Gegeven is de functie f共x兲 ⫽ 1 ⫹ sin 共x ⫹ 31 ␲兲.
Teken de grafiek op het interval 关⫺␲, 2␲兴.
Welke periode heeft de grafiek van f?
Bereken met behulp van de periode en de horizontale verschuiving
bij welke waarden van x de symmetrieassen liggen.
Los de vergelijking 1 ⫹ sin 共x ⫹ 31 ␲兲 ⫽ 1 21 op 关⫺␲, 2␲兴 exact op.
d
8
a
b
c
d
e
Hiernaast zie je op het interval 关⫺2␲, 2␲兴 de
grafieken van de functies f共x兲 ⫽ 2x ⭈ sin x en
g共x兲 ⫽ x.
Bereken f 共 61 ␲兲 exact.
Bereken f 共 31 ␲兲 exact.
Om de coördinaten van de snijpunten van beide
grafieken te berekenen, moet je de vergelijking
2x ⭈ sin x ⫽ x oplossen.
Deze vergelijking is gelijkwaardig met
x ⫽ 0 of 2sin x ⫽ 1. Leg dat uit.
Los de vergelijking 2x ⭈ sin x ⫽ x exact op.
Geef de exacte coördinaten van de vijf snijpunten
die hiernaast te zien zijn.
y
5
4
3
f
2
1
–7
–2π
–6 –5
–π
–4 –3 –2
π
–1 O
–1
1
2
3
4
5
6
2π
x
7
–2
g
–3
–4
–5
–6
–7
–8
–9
–10
9
a
b
c
10
a
b
c
d
e
Los de volgende vergelijkingen op het gegeven
interval exact op.
4x ⭈ cos x ⫽ x ⭈ 2冪2 op 关0, 2␲兴
2x 2 ⭈ sin 2x ⫽ x 2冪3 op 关⫺␲, ␲兴
6x ⭈ cos x ⫹ 3x ⫽ 0 op 关9␲, 12␲兴
De grafiek van functie f共x兲 ⫽ 2x ⭈ sin x uit opdracht 8 lijkt
een top te hebben bij x ⫽ 2.
Als de grafiek van f een top heeft bij x ⫽ 2, dan moet f ⬘共2兲 ⫽ 0.
Gebruik de productregel om de afgeleide van f te berekenen.
Bereken f ⬘共2兲 en laat zien dat f ⬘共2兲 ⬎ 0.
Ligt de genoemde top links of rechts van x ⫽ 2?
Ga na dat de exacte waarde van de helling van de grafiek
van f in het punt 共 61 ␲, 61 ␲兲 gelijk is aan 1 ⫹ 61 ␲冪3.
Bereken de exacte waarde van de helling van de grafiek
van f in het punt 共 41 ␲, 41 ␲冪2兲.
© Noordhoff Uitgevers bv