hoofdstuk 2 functies

netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
hoofdstuk 2 functies
kern 1 grafische rekenmachine
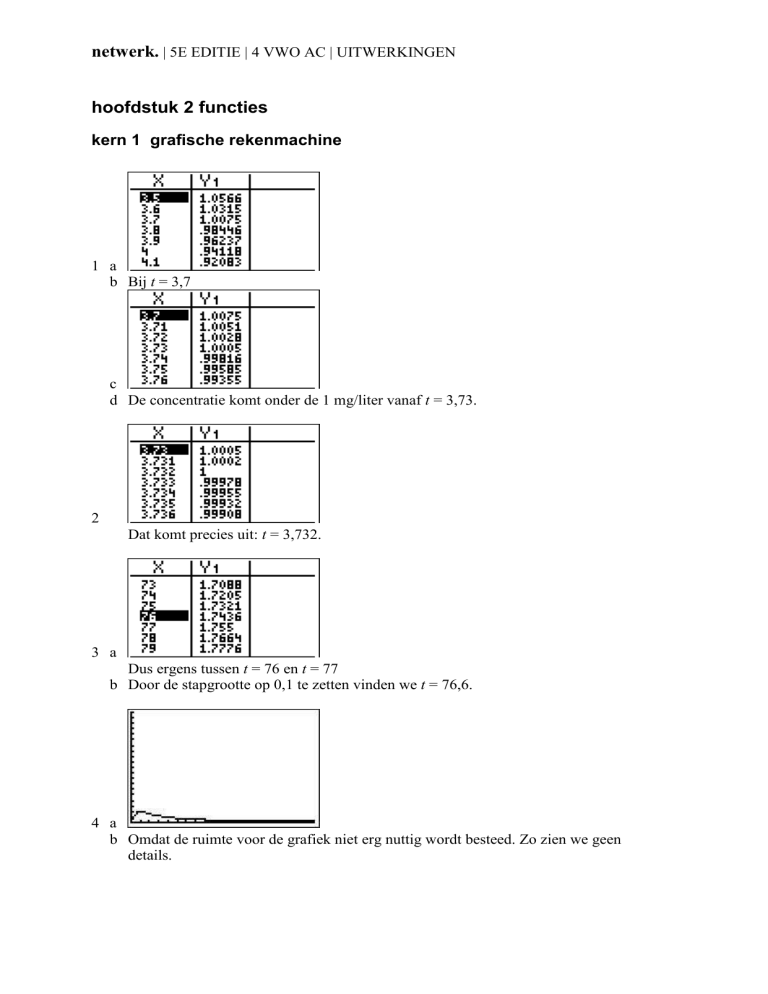
1 a
b Bij t = 3,7
c
d De concentratie komt onder de 1 mg/liter vanaf t = 3,73.
2
Dat komt precies uit: t = 3,732.
3 a
Dus ergens tussen t = 76 en t = 77
b Door de stapgrootte op 0,1 te zetten vinden we t = 76,6.
4 a
b Omdat de ruimte voor de grafiek niet erg nuttig wordt besteed. Zo zien we geen
details.
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
c
d Dit lijkt net een lineaire functie want je ziet een rechte lijn.
e Omdat het niet gebruikelijk is negatieve tijden te beschouwen.
5 a
b De kleinste functiewaarde vinden we voor x  2 namelijk 5, 6 en de grootste
voor x  6 namelijk 7,2.
c
d
e De grafiek gaat door O, en snijdt de x-as verderop nog een keer, dus twee
nulpunten.
(Voor x = 0 is de functiewaarde
0, dus dat lijkt niet alleen een nulpunt,
maar is het ook
echt.)
f De functie heeft 2 extremen.
6 a
[−10, 10] × [−25, 10]
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
b
[−5, 5] × [−2, 5]
c
[−10, 10] × [−50, 50]
d
[−0, 5] × [−0, 1]
7 a 85,5625 cm
b 100 cm
c 126,5625 cm
8 a
[−5, 5]× [−10, 20]
b Nulpunt ligt bij x = −2. De toppen bij (−1, 10) en (0,56; 4,35)
9 a In het midden van de brug is (zie tekening) x = 0. h(0)  7225  75  10 meter.
b Dit kunnen we oplossen door de grafiek te plotten en de nulpunten op te zoeken. We
vinden voor deze nulpunten x = 40 en x = −40. De brug is dus 80 m breed.
kern 2 domein en bereik
10 a Omdat we dan de wortel van −5
moeten nemen en die bestaat niet.
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
b We moeten dus voorkomen dat het getal onder de wortel kleiner dan 0 wordt.
x 2  4 geeft dat 2  x  2 .
11 a 3  x  1
 3,1
b 1,3  x  5
1,3;5
c x  1 en x  2
, 1   2, 
d x0
e x 1
f 0  x  3 en 4  x  6
g
 2,2
h  3, 
i
,0  0, 
12 a Omdat we dan de wortel uit een negatief getal moeten nemen.
b
c
d Nee
13 a
1
2
x20
x  2
x  4
1
2
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
Het domein is dan D f   4, 
b
c Nee, de grafiek van g is 4 naar beneden geschoven in vergelijking met f.
14 a y1:
2x  3  0
2x  3
x  23
Het domein is dan D y1   23 , 
y2:
2 x  3  0
2 x  3
2x  3
(We vermenigvuldigen met −1, dus we moeten het ongelijkheidsteken
omdraaien.)
x  23
Het domein is dan D y2   , 23 
b
15 a
x kan hier alle waarden aannemen, dus D f 
b
2 x 0
.
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
2 x
x2
Het domein is dan Dg   ,2
c
x0
Het domein is dan D y1  0, 
d
Hier kan x wederom alle waarden aannemen, dus Dk 
met ongelijkheidstekens weergeven.
. Dat kunnen we niet
16 a Als we in de grafiek kijken lijkt het of het maximum bij x = 2 moet liggen. Enig
narekenen bevestigt dit vermoeden. De functie heeft dan de waarde 2.
b
17 a
b Voor de wortel moet gelden: x  0 . Daar heeft f de waarde 2. Het bereik is dan
B f   2,  .
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
c Nee, deze is twee naar rechts geschoven.
18 a Uit de grafiek lijkt het minimum bij x  2 te liggen. Dit klopt. De
corresponderende functiewaarde is −4. Het bereik is dan B f   4,  .
b De maximumwaarde voor x is x  2 . Dit correspondeert met een functiewaarde 4.
Aangezien het een dalende functie is, is het bereik Bg   ,4 .
c De minimum waarde voor x is x  0 . Dit correspondeert met een functiewaarde 0.
Aangezien het een stijgende functie is, is het bereik Bh  0,  .
d Hoe klein x ook wordt, de waarde k  0 zal nooit bereikt worden. Het bereik is
dan Bk  0,  .
19 a Aangezien er een minteken voor de hoogte h staat, wordt het kouder naarmate je
hoger komt.
b Dit komt door de samenstelling van de atmosfeer.
c T 1  20  6  14 en T 1  20  6  12  52 . Dus BT  14, 52 . De
temperatuur tussen 1 en 12 km hoogte ligt dus tussen de 14 en −52 graden
Celsius.
d Dan moet we oplossen 20  6h  0 .
20  6h  0
20  6h
h  206  3,333
Dus dat is na 3333 meter.
kern 3 asymptoten
20 a Een oppervlakte O rekenen we uit met lengte × breedte, O  l  b . We weten dat
O 6
hier O = 6. De breedte kunnen we dus berekenen met b  l    .
l
l
lengte l (cm)
1
2
3
6
10
20
30
60
breedte b (cm)
6
3
2
1
0,6
0,3
0,2
0,1
b
6
. (We laten alleen de positieve waarden voor de lengte
l
en breedte zien, aangezien de negatieve waarden geen betekenis hebben.)
c Die wordt steeds kleiner.
De functie is dus b  l  
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
21 a
b
c f: verticale asymptoot x  0 en horizontale asymptoot y  0
g: x  0 en y  3
h: x  3 en y  0
22 a
b De x- en y-as.
c Als de prijs oneindig hoog wordt ( p   ), zal niemand het product meer willen
of kunnen kopen, q  0 .
d Als de prijs naar 0 gaat, zal de verkoop naar oneindig gaan.
23 a Daar hebben we uiteraard geen GR voor nodig, want we kunnen simpelweg
bekijken of als t = 0 de functiewaarde ook 0 is. Dat is niet het geval:
200  0
 20  20 ). Dus nee.
( T (0) 
0 1
200  10
 20  181,82  20  201,82 graden.
b T (10) 
10  1
c Dus, wat is de horizontale asymptoot van deze grafiek? Dat kunnen we met de GR
uitzoeken. Dat geeft 220 graden.
24 a
b
c
d
e
Dan gaat de functiewaarde naar 3.
Dan gebeurt er hetzelfde.
Uit a en b leren we dat de asymptoot bij y  3 ligt.
Nee die bestaat niet
De functie kan alle waarden aannemen, behalve y  3 . Dus het bereik is
B f  ,3  3,  .
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
25 a
20  0  80
 80 , dat wil zeggen 80 graden. Dat
0 1
klopt met wat we in de grafiek zien.
c De buitentemperatuur is de horizontale asymptoot van de grafiek en die ligt bij 20
graden.
b Dat is op het tijdstip t = 0. T  0  
26 a Voor x  3 krijgen we een 0 in de noemer, en dan is er geen y-waarde.
b Alle waarden van x zijn goed, behalve x  3 . Dus het domein is
D f  ,3  3,  .
c −10 en −100
d 10 en 100
e Afhankelijk of je een waarde groter (vraag d) of kleiner (vraag c) dan 3 hebt
genomen, wordt de functiewaarde steeds groter of steeds kleiner.
27 a De noemer mag niet 0 worden, dus 2 x  4  0 . Dit geeft 2 x  4 en x  2 .
b Uit opgave a vermoeden we dat aangezien x  2 , x  2 de verticale asymptoot
van de functie is. Onderzoek met de GR bevestigt dit vermoeden.
28 a De noemer mag niet 0 worden, dus x  2 . Dit geeft het domein
D g  , 2  2,  .
b Voor de waarde x  2 is de teller toevallig ook 0. Voor x-waarden dicht in de
buurt van 2 wordt de y-waarde 4. Er zit een “gaatje” in de grafiek.
29 a De noemer mag niet 0 worden, dus 2 x  5  0 . Dit geeft 2 x  5 en x  2,5 .
b De verticale asymptoot is x  2,5 .
c De horizontale asymptoot is y  2 . (Die kunnen we vinden door hele grote of
juist hele kleine waarden voor x in de functie in te vullen. Of door te bedenken dat
de −5 in de noemer weg gaat vallen voor grote of kleine x, dus dat de functie dan
2 geeft.)
d
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
kern 4 grafieken verschuiven
30 a De onderste grafiek lijkt naar 0 te gaan voor grote x, dat correspondeert dus met
1
y .
x
b Dat is nu niet zo'n moeilijke vraag meer. En het klopt ook, want we zien hier een
horizontale asymptoot die niet bij y = 0 ligt.
31 a h 8  5  82  40  8  8  (5  8  40)  8  0  0
b Dan tellen we er simpelweg 45 bij op: h  5t 2  40t  45
32 a
b
c
d
e
Door f twee naar beneden te verschuiven.
1  2x 1 2x 1
 
  2 . Dan zien we gelijk
We kunnen g herschrijven als g  t  
x
x x
x
de verschuiving.
Door f drie naar boven te verschuiven.
3x  1
1
h t  
 3
x
x
f: HA y  0 en VA x  0
g: HA y  2 en VA x  0
h: HA y  3 en VA x  0
33 a Aannemende dat de linker verticale streep in het plaatje de y-as voorstelt en de
1
rechter streep een asymptoot, hoort de linker grafiek bij y  aangezien deze
x
functie een verticale asymptoot bij x  0 heeft.
1
b y
heeft een asymptoot bij x  2 . Dat klopt dus mooi met het plaatje.
x2
34 a De grafiek is 2 naar links verschoven.
b f ( x)  ( x  2)2 . Controle: f ( 2)  ( 2  2)2  0
c Vier naar links en vier naar beneden.
d g ( x )  x  4  4 . Controle: g ( 4)  4  4  4  4
x
4
x5
x2
b h( x ) 
x7
35 a g ( x ) 
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
x 5
x 5
1 
1
( x  5)  5
x
d f: VA: x  5 (Dan wordt de noemer nul.)
HA: y  1 (x heel groot, dan valt de factor 5 eruit en x/x = 1)
Voor de andere functies kunnen we de asymptoten voor f gebruiken en ze
simpelweg verschuiven. Een links- en rechtsverschuiving beïnvloedt alleen de
verticale asymptoot ( y  …) en een boven- en benedenverschuiving de
horizontale asymptoot ( x  …).
g: VA x  5 en HA y  1  4  3
h: VA x  5  2  7 en HA y  1
k: VA x  5  5  0 en HA y  1  1  2
c k ( x) 
test
36 a We kunnen simpelweg de x-waarden uit de grafieken aflezen. De dichte rondjes
geven aan dat de waarden er nog wel bij horen.
functie I: D1   2,2
functie II: D2  , 1  1, 
functie III: D3  ,0  0,  
b functie 1: 1  y  4 (Het blijft een beetje een gok met het aflezen uit grafieken.
We kunnen bijvoorbeeld niet zeker weten of de waarde y = −1 ook daadwerkelijk
gehaald wordt als we het functievoorschrift niet hebben. Laten we er maar van
uitgaan.)
functie 2: y  0
functie 3: y  0 en y  2
37 a
tijd t (dagen)
0
1
2
3
4
hoogte H (dm)
4
4,3
4,42
4,52
4,6
We moeten oplossen 4  0,3 t  6 . Dit geeft
0,3 t  2
2
t
 6,67
0,3
t  44,44 oftewel na zo’n 45 dagen.
b
We moeten oplossen 4  0,3 t  8 . Dit geeft
0,3 t  4
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
4
 13,33
0,3
t  177,78 oftewel na zo’n 178 dagen.
t
38 a f: Wat onder de wortel staat moet gelijk of groter nul blijven: 2 x  5  0 geeft
2 x  5 dus het domein is x  2,5 . Dit is een stijgende functie. Dus voor de
laagst mogelijke waarde van x (namelijk 2,5) vinden we de laagst mogelijke
functiewaarde: f ( 2,5)  1 en het bereik is dan ook B f   1,  .
g: x  7 . Nu is het echter een dalende functie (vanwege het minteken), dus de
minimale functiewaarde vinden we door de maximale x-waarde in te
vullen: g (7)  0 en het bereik is dan Bg  0,  .
b
39 a De noemer mag niet nul worden, dat geeft de VA x  2 . De HA asymptoot is
y  1 .
b
40 a
b
c
f ( x)  x  3
f ( x)  ( x  2)2  4( x  2)
3( x  5)
3x  15
f ( x) 

( x  5)  7
x2
41 a 1 naar rechts
2 x  1 2 x  2  1 2( x  1)  1 2( x  1)
1
1




 2
b h( x ) 
x 1
x 1
x 1
x 1
x 1
x 1
c 2 omhoog, 1 naar rechts
d Asymptoten van f zijn simpel: VA x  0 en HA y  0 . Dit van de andere kunnen
we vinden door deze asymptoten te verschuiven.
g: VA x  1 en HA y  0 .
h: VA x  1 en HA y  2 .
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
herhaling
42 a
b
c
d
43 a
b H  0 
20  0  5 5
  1 . 1 meter dus.
05
5
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
c
d Uit de tabel zien we dat dat 13,667 – 12,692 = 0,975 meter is.
e Zelfde methode geeft 0,588 meter. De boom gaat dus langzamer groeien. Dit zien
we ook in de grafiek, stijgt steeds minder.
f
Na 14 jaar dus.
g 20 meter
44 a De VA is x  5 (dan wordt de noemer nul) en de HA is y  20 (Dat weten we
uit vraag 43g).
b De enige waarde van x die niet mag, is x  5 . Het domein is dan ook
D f  , 5  5,  .
c Er is een HA bij y  20 . Het bereik is dan ook B f  , 20  20,  of, met
ongelijkheidstekens, y  20 .
45 a
b
f 8  2  8  4  4(4  1)  2 5  4,47
g  8  4  2  8  4  4  8
Dus het verschil is ongeveer 3,53.
c Nee.
d Nee dus.
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
46 a
b [0, 85] bij [0, 20]
c Dus wanneer is h = 0? Dat is simpel te zien, namelijk bij a = 80 (en bij a  0
natuurlijk.)
d Dat is halverwege, bij a = 40. h(40)  0,01  40  (80  40)  0,01 1600  16 .
e Dat is op a = 15,5 en a = 64,5.
f Omdat de bal niet onder de grond kan komen en de maximale hoogte 16 meter is,
is het bereik Bh  0, 16 . Het domein is Dh  0, 80 , wat de minimale en
maximale afstand van de bal is.
47 a
b
c
d
Uit de grafiek zien we VA x  4 en HA y  2 . Dat klopt met de functie.
x  4,57
x  4
D f  , 4  4,  want x  4 is de enige niet toegestane waarde.
B f  ,2  2,  want y  2 is de enige functiewaarde die nooit wordt bereikt.
48 a
b
f 2 ( x)  2 x  3
c g2 ( x )  2 x  4  4
d D f  0,  en B f  0, 
D g   2,  en Bg  0, 
e D f 2  0,  en B f 2  3, 
D g2   2,  en Bg 2   4, 
49 a h( x)  2( x  2)  2 x  4 , dus van de oude grafiek g.
b Ja dus.
c i( x)  2 x  3
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
j( x)  2( x  2)  3  2 x  4  3
Of:
i2 ( x)  2 x  4
j2 ( x)  2 x  4  3
Ja dus.
50 a
b
x  2
4
x6
2
2
f3 ( x) 
44 
( x  1)
x 1
f2 ( x) 
51 a
b Voor beide grafieken zijn alle x waarden toegestaan, dus voor beide geldt D =
Verder kan f de waarde nul wel bereiken, en g niet. Dus D f  0,  en
D g  0,  .
c f(3) = 0, dus x = 3 is het nulpunt. Toevalligerwijs is dit ook waar het minimum
van de functie ligt. Aangezien g de x-as nooit bereikt wordt, heeft hij geen
nulpunt, maar wel een horizontale asymptoot bij y = 0. g heeft geen extremen.
d 0,002( x  3)2  5
( x  3)2  2500
x  3  50
x  3  50
Dus voor f is x  47 of x  53 .
Voor g zoeken we met onze GR en vinden x  35,4 .
doorwerking
52 a Omdat de automobilist in 0,8 seconden een afstand van 0,8v meter aflegt voordat
v2
hij begint met remmen. Dit moeten we er dus bij optellen: s  0,8v  .
12
b 130 km/u = 130 (1000 m/3600 s) = 130/3,6 m/s = 36,11 m/s.
Dus voor het x-bereik nemen we [0, 40] wat correspondeert met een y-bereik van
.
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
[0, 170].
c 30 km/u = 30/3,6 m/s = 8,33 m/s. s 8,33  0,8  8,33 
d 0,8v 
8,332
 12,45 meter.
12
v2
 65 oplossen geeft v = 23,54 m/s, oftewel v = 23,54 × 3,6 = 84,7 km/u.
12
53 a D f  [0,8]
b Dat ligt halverwege het domein dus bij x = 4. f (4)  8  4  42  2 8  4  4 .
c x  7,64 en x  0,54 .
54 a y  f ( x ) 
150
x2
150
 16,67 : lengte is dus 16,67 dm en de breedte en hoogte zijn elk 3 dm.
9
150
f (10) 
 1,5 : lengte is dus 1,5 dm en de breedte en hoogte zijn elk 10 dm.
100
c 100 cm is 10 dm. Dus in ieder geval x  10 . Nu is f(10) = 1,5, en als x kleiner of
gelijk aan 10 moet zijn, is f ( x )  y  1,5 . Dit geeft voor y 1,5  y  10 . Verder,
b
f (3) 
als y = 10, dan x  150 / 10  3,87 . Dit geeft voor x 3,87  y  10 .
 150 
 150 
55 a 12  
  3  12  
  3  30 . De punten (−150, 30) en (150, 30) liggen
 100 
 100 
in ieder geval op de parabool. De palen zijn 30 meter hoog, dus dit klopt!
b De parabool heeft zijn minimum voor x = 0. In dat punt is de waarde van y = 3
meter. Dus aan de tweede eis voldoet de kabel, maar aan de eerste zeker niet.
c We zien gelijk dat het minimum nu 16,5 meter is. Nu is het goed.
d 76,4
2
2
vaardigheden
56 a
 2 
3
  3    2    3  8  9  17
2
3
2
b 10  5  62  5  2  36  5  34  (150  20)  170
c 3   24    2  3  24  24  24 (3  1)  16  4  64
4
d 72  122  49  144  (144  49)  95
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
57 a 7 15  1 12  7 102  1 105  8 107
5
7
b 7 15  1 12  7 15  1  12  6 15  12  6 102  105  5 12
10  10  5 10
c 7 15  1 12  365  23  3  185  545  10 54
d 7 15 :1 12  365 : 23  365  23  2  125  245  4 45
e 3 13  4 12  3 62  4 63  7 65
f 3 13  4 12  103  92  206  276   76
g 3 13  4 12  103  92  906  150
20
h 3 13 : 4 12  103 : 92  103  92  27
58 a
b
c
d
e
f
8,356  106
5,7  10
9  109
6,4 103
2,3 107
3,24667 105
59 a
b
c
d
536 000
0,0000536
83 000 000
0,083
61 a Een uur bevat 3600 seconden, en 3600 s  2,988 108 m/s = 1,07928 1012 m .
b 1,07928 1012 m = 1,07928 1012 km/1000 = 1,07928 109 km .
62 a In mm nauwkeurig betekent hier dat we 1 decimaal moeten geven (1 mm = 0,1
cm). De omtrek is 2  8 cm  50,3 cm .
b  (4 cm)2  50,27 cm2 . Hier moeten we 2 decimalen geven want 1 mm2 = 0,01
cm2.
c 644 cm  2 r
r  102,5 cm (Wederom 1 decimaal, net als in a.)
d 644 cm 2   r 2
644
r2 
cm 2  204,99 cm 2

r  14,32 cm
De omtrek is dan 2  14,32 cm = 90,0 cm
63 a Van de bovenste helft 2 van de 3, dus 23 , en van de onderste 3 van de 7, dus 73 . Als
23
we dat optellen en door twee delen, vinden we 42
.
b
64 a
23
42
    2 cm   6,88 cm 2 .
2
1
1
p 1 1 p
1
p 1
p
p 1 p
1


  




p p  1 p  1 p p p  1 p( p  1) p( p  1) p( p  1) p( p  1)
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
b
2
3
2( x  3)
3( x  1)




x  1 x  3 ( x  1)( x  3) ( x  1)( x  3)
2( x  3)  3( x  1) 2 x  6  3x  3
5x  3


( x  1)( x  3)
( x  1)( x  3) ( x  1)( x  3)
c
2t
t 3
2t (2t )
(t  3)2 (2t )2  (t  3)2 (2t )2  t 2  9  6t 5t 2  9  6t






t  3 2t
(t  3)2t (t  3)2t
(t  3)2t
(t  3)2t
(t  3)2t
a
5
a(a  5)
5(a  5)
a 2  5a  5a  25 a 2  25
d




 2
a  5 a  5 (a  5)(a  5) (a  5)(a  5)
(a  5)(a  5)
a  25
2
2
5 q
5  q (2q)
4q  5  q
e
 2q 


2q
2q
2q
2q
1
6 x
1
5 x



f 1
6 x 6 x 6 x 6 x
y
26
4


  12 . b berekenen we met behulp van
x 5  ( 3) 8
het eerste punt: 6   12 ( 3)  b geeft b  6  23  4 12 . Dit geeft y   12 x  4 12 .
y 2  6  4


  12 . b zien we gelijk uit punt A. Dit geeft
b Het hellingsgetal a 
x 8  0
8
y   12 x  6 .
y 3  ( 2) 5 1
c Het hellingsgetal a 


 2 . b berekenen we met behulp van het
x 5  ( 5) 10
eerste punt: 2  12 ( 5)  b geeft b  2  25  12 . Dit geeft y  12 x  12 .
y
28
6
d Het hellingsgetal a 


  23 . b berekenen we met behulp van
x 8  ( 1) 9
het eerste punt: 8   23 ( 1)  b geeft b  8  23 ( 1)  7 13 . Dit geeft y   23 x  7 13 .
65 a Het hellingsgetal a 
66 a 2 x  5  3
2 x  3  5  8
x  4
b x 2  4  3
x 2  3  4  1
x  1 of x  1
c (2 x)2  11  3
(2 x)2  3  11  8
2 x   8   4  2  2 2
x  2 of x   2
d 6x  6  3
6x  3  6  9
6x  9
x  23
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
9
 3
x
9  3x
9
x
 3
3
16
 11  3
f
x
16
 3  11  8
x
16  8x
x2
e
67 a 2 x  3  x  5
2x  x  2
x2
b 4 x  3  3x  4
4 x  3x  7
x7
c 3 x 2  147
x 2  49
Eerst de bijhorende vergelijking oplossen levert x  7 of x  7 . Voor de
ongelijkheid geeft dit x  7 en x  7 .
d 18  2 x 2  0
18  2x 2
9  x2
x2  9
Eerst de bijhorende vergelijking oplossen levert x  3 of x  3 . Voor de
ongelijkheid geeft dit 3  x  3 .
e 14 x  3 14  16
1
1
4 x  19 4
x  77
f  13 x 2  12
x 2  12 (Bij het vermenigvuldigen met een negatief getal klapt het
ongelijkheidsteken om.)
x 2  36
Eerst de bijhorende vergelijking oplossen levert x  6 of x  6 . Voor de
ongelijkheid geeft dit x  6 en x  6 .
1
3
68 a x 2  30
x   30
b ( x  6)2  30
( x  6)   30
x  6  30
c 8 x 2  96
x 2  12
netwerk.  5E EDITIE  4 VWO AC  UITWERKINGEN
x   12   3  4  2 3
d 3( x  5)2  48
( x  5)2  16
( x  5)  4
x  4  5
x  1 of x  9