Gebroken functie

Gebroken functie
© Wisnet-HBO
update mei 2010
1 Inleiding
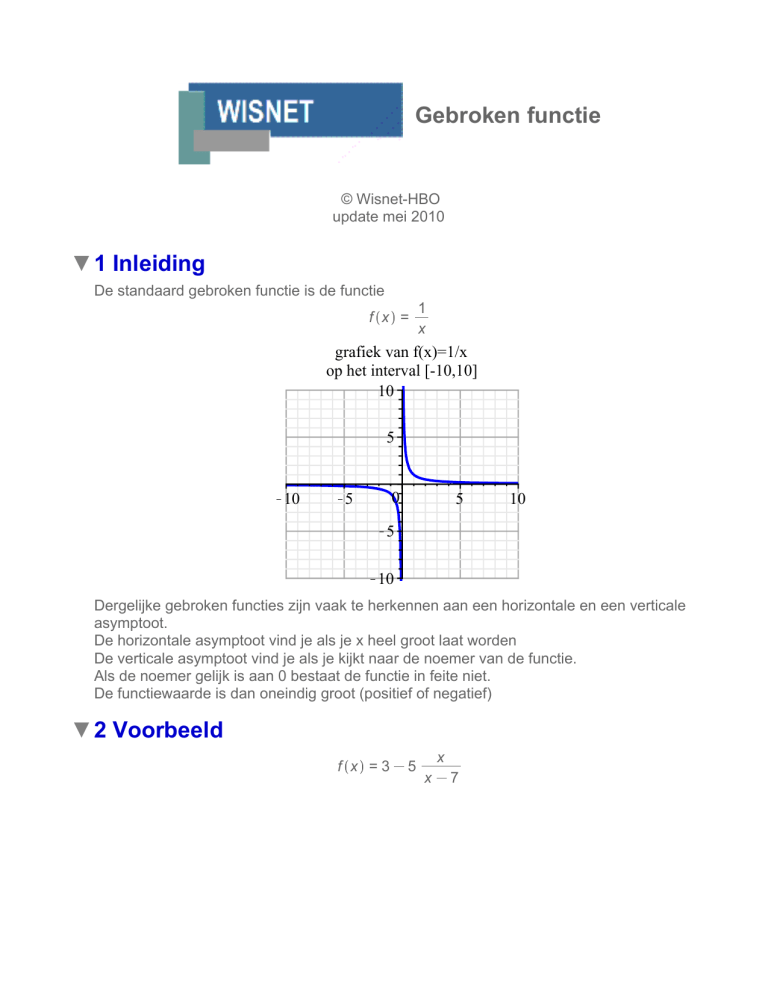
De standaard gebroken functie is de functie
f x =
1
x
grafiek van f(x)=1/x
op het interval [-10,10]
10
5
10
0
5
5
10
5
10
Dergelijke gebroken functies zijn vaak te herkennen aan een horizontale en een verticale
asymptoot.
De horizontale asymptoot vind je als je x heel groot laat worden
De verticale asymptoot vind je als je kijkt naar de noemer van de functie.
Als de noemer gelijk is aan 0 bestaat de functie in feite niet.
De functiewaarde is dan oneindig groot (positief of negatief)
2 Voorbeeld
f x =3
5
x
x
7
20
10
20
10 5 0
5 10 15 20 25 30
10
20
Merk de volgende eigenschappen op:
• Als x = 7 , dan zie je een verticale asyptoot.
Immers de noemer van de breuk is gelijk aan 0
• Als x
, dan zie je een horizontale asymptoot y = 2
x
Immers de vorm
nadert tot 1 als x
.
x 7
• Als x = 0, dan is de functiewaarde gelijk aan 3.
Je ziet dus duidelijk dat de grafiek door het punt (0, 3) gaat.
3 Voorbeeld
f x =
15
x
5x
7
20
10
20
10
0
10
20
10
20
30
Merk de volgende eigenschappen op:
• Als x = 7 , dan zie je een verticale asyptoot.
Immers de noemer van de breuk is gelijk aan 0
• Als x
, dan zie je een horizontale asymptoot y = 5
15 5 x
Immers de vorm
nadert tot -5 als x
.
x 7
• Als x = 0, dan is de functiewaarde gelijk aan
door het punt
0,
15
7
15
. Je ziet dus duidelijk dat de grafiek
7
gaat.
• Als x = 3, dan is de functiewaarde gelijk aan 0. (Immers de teller van de breuk is dan 0.
Je ziet dus duidelijk dat de grafiek door het punt 3 , 0 gaat.
4 Voorbeeld
Gegeven is een gebroken functie
bx 7
dx c
Hierbij is gegeven dat de grafiek een verticale asymptoot heeft:
2
x=
7
7
11
De grafiek gaat verder nog door de punten 0,
en 1,
.
2
9
Bereken dan de waarden b, c en d.
f x =
4.1 oplossing
Gegeven is een gebroken functie
bx 7
dx c
Hierbij is gegeven dat de grafiek een verticale asymptoot heeft:
2
x=
7
7
11
De grafiek gaat verder nog door de punten 0,
en 1,
.
2
9
Bereken dan de waarden b, c en d.
De gegevens zijn te interpreteren tot drie vergelijkingen met drie onbekenden.
Stel eerst de drie vergelijkingen op.
2
• De noemer is gelijk aan 0 als x =
dus de eerste vergelijking wordt:
7
2
d
c = 0.
7
f x =
• Eerste punt 0,
7
7
7
invullen dus x = 0 invullen in de functie:
= .
c
2
2
• Tweede punt 1,
11
9
invullen dus x = 1 invullen in de functie:
b
d
7
11
=
.
c
9
De drie vergelijkingen zijn dus
2
d
7
c =0
7
7
=
2
c
11
7
=
c
9
b
d
De drie vergelijkingen herschrijven zonder breuken:
2d
7 c =0
c =2
9 b
7 = 11 d
c
Verder herleiden
2d
7 c =0
c =2
9b
63 = 11 d
11 c
Dan c = 2 bijvoorbeeld invullen in de eerste vergelijking en d berekenen.
Invullen in de derde vergelijking en b berekenen.
b=4
c=2
d=7
De functie is dus
4x 7
f x =
7x 2
10
5
4
0
2
2
4
5
10
5 Voorbeeld
Gegeven is een gebroken functie
bx 3
dx 6
Hierbij is gegeven dat de grafiek een verticale asymptoot heeft:
x= 2
8
De horizontale asymptoot is y = .
3
Bereken dan de waarden b en d.
f x =
5.1 oplossing
Gegeven is een gebroken functie
bx 3
dx 6
Hierbij is gegeven dat de grafiek een verticale asymptoot heeft:
x= 2
8
De horizontale asymptoot is y = .
3
Bereken dan de waarden b en d.
f x =
De gegevens zijn te interpreteren tot twee vergelijkingen met twee onbekenden.
Stel eerst de twee vergelijkingen op.
• De noemer is gelijk aan 0 als x = 2 dus de eerste vergelijking wordt: d
2
6 = 0.
• Als x
dan krijgt de functie ongeveer de waarde
b
.
d
De drie vergelijkingen zijn dus
2d
6 =0
8
b
=
3
d
De twee vergelijkingen herschrijven zonder breuken:
2d
6 =0
3 b =8 d
Verder herleiden
d =3
3 b = 24
Dan d = 3 invullen in de tweede vergelijking en b berekenen.
b=8
d=3
De functie is dus
f x =
8x
3x
3
6
10
5
10
5
0
5
10
5
10