de formule y = a/x + b

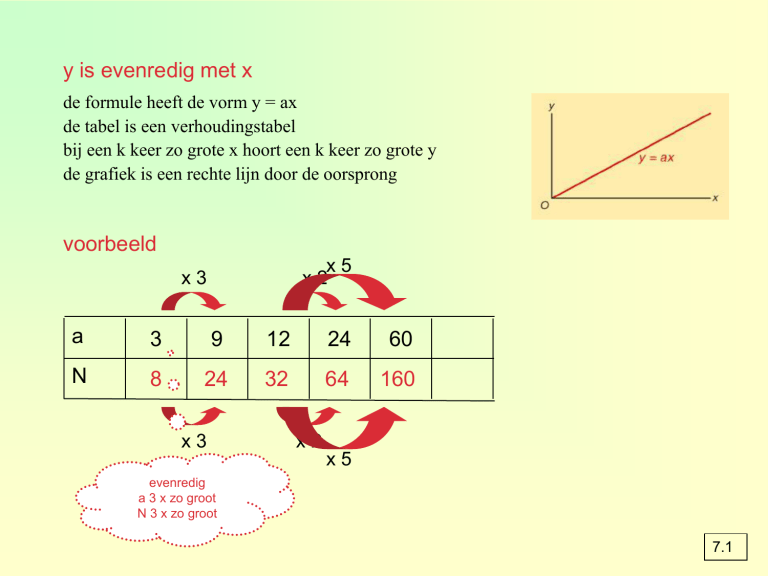
y is evenredig met x
de formule heeft de vorm y = ax
de tabel is een verhoudingstabel
bij een k keer zo grote x hoort een k keer zo grote y
de grafiek is een rechte lijn door de oorsprong
voorbeeld
x5
x2
x3
a
3
9
12
24
60
N
8
24
32
64
160
x3
x2
x5
evenredig
a 3 x zo groot
N 3 x zo groot
7.1
y is omgekeerd evenredig met x
de formule heeft de vorm xy = a , ofwel y = a/x
vermenigvuldig je x met een getal,
dan moet je y door dat getal delen
de grafiek is een hyperbool
voorbeeld
x2
P
3
4
8
9
36
T
24
18
9
8
2
:2
vermenigvuldigd
steeds 72
omgekeerd evenredig
P 2 x zo groot
T 2 x zo klein
7.1
Asymptoten
2
de grafiek van y = komt steeds dichter bij de
x
x-as
de x-as is een asymptoot van de grafiek
een asymptoot is een lijn waar een grafiek op den
duur mee samenvalt
de x-as is de horizontale asymptoot
de y-as is de verticale asymptoot
2
de grafiek van y = + 5 ontstaat uit die van
x
2
y = door deze 5 omhoog te verschuiven
x
2
de grafiek van y = + 5 heeft daarom de lijn y = 5
x
als horizontale asymptoot
de lijn x = 0 is de verticale asymptoot
komt heel dicht bij de x-as
7.2
Algemeen
7.2
Grafieken tekenen
werkschema : de grafiek van een formule tekenen
1 voer de formule in op de GR
2 kies een geschikt venster zo, dat het verloop van de grafiek goed zichtbaar is
3 maak een tabel op de GR en zet de tabel in je schrift
4 gebruik de punten uit de tabel om de grafiek nauwkeurig te tekenen
7.2
Algemeen
de formule y = a/x
• de lijn y = 0 (x-as) is de horizontale asymptoot
• de lijn x = 0 (y-as) is de verticale asymptoot
de formule y = a/x + b
de grafiek ontstaat uit die van y = a/x door de grafiek b
omhoog te verschuiven
• de lijn y = b is de horizontale asymptoot
• de lijn x = 0 (y-as) is de verticale asymptoot
de formule R = a/t + b
• de lijn R = b is de horizontale asymptoot
• de lijn t = 0 is de verticale asymptoot
7.2
Een machtsformule heeft de vorm y = axn
n even
y
n oneven
y
x
O
a >0
de top is (0,0)
O
a< 0
y
x
O
a >0
y
x
O
x
a< 0
het punt van symmetrie is (0,0)
7.3
de grafiek van y = axn met a > 0 is
• toenemend stijgend voor n > 1
• afnemend stijgend voor 0 < n < 1
• afnemend dalend voor n < 0
v.b.
n>1
0<n<1
n<0
7.3
Evenredig en omgekeerd evenredig met een macht van x
als de grootheden P en Q evenredig zijn, bestaat er een getal a zo, dat P = aQ
het getal heet de evenredigheidsconstante
en zo volgt uit
y is evenredig met x0,75
dat er een getal a bestaat zo, dat y = ax0,75
y is evenredig met xn betekent dat er een getal a bestaat met y = axn
voor omgekeerd evenredig geldt een dergelijke eigenschap
y is omgekeerd evenredig met xn betekent dat er een getal a bestaat
met y = a/xn
7.3
Evenredigheid aantonen bij tabellen
werkschema : hoe volgt uit een tabel met onderzoeksresultaten dat y
evenredig is met xn ?
y
bereken bij elk onderzoeksresultaat het quotiënt
xn
laat zien dat deze quotiënten gelijk zijn
in het geval de quotiënten (bij benadering) gelijk zijn, weet je de
evenredigheidsconstante a en dus ook de formule y = axn
7.3