EXTRA BLOK 4 MECHANICA

EXAMENTRAINING
I
BLOK 4 MECHANICA
HET BALLETJE
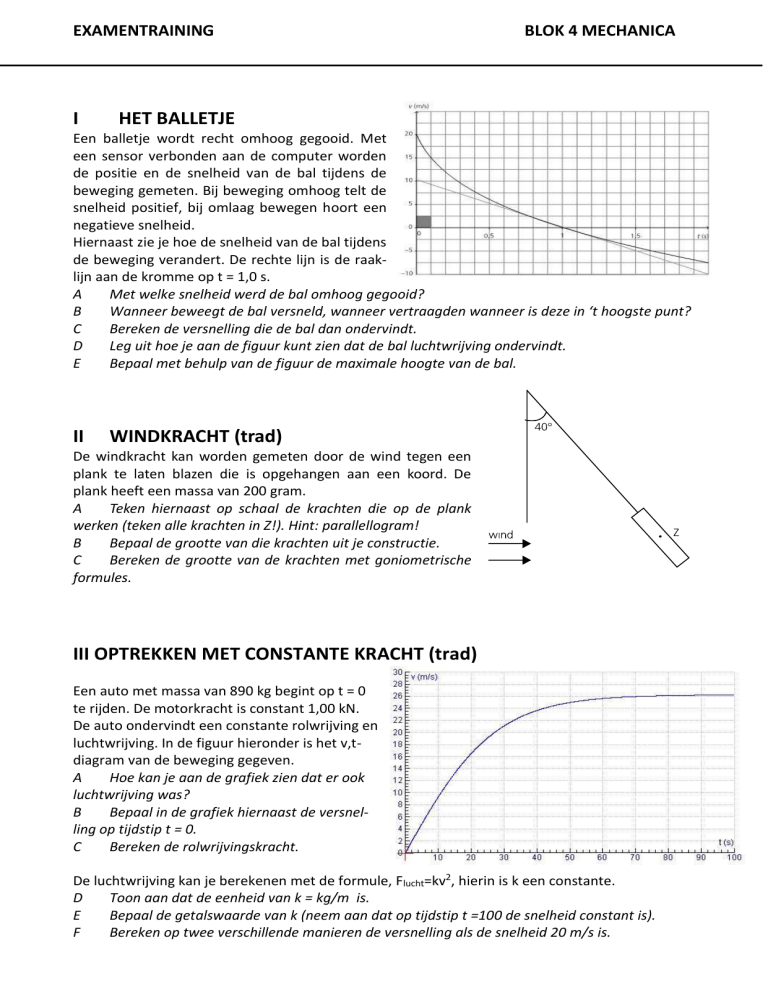
Een balletje wordt recht omhoog gegooid. Met
een sensor verbonden aan de computer worden
de positie en de snelheid van de bal tijdens de
beweging gemeten. Bij beweging omhoog telt de
snelheid positief, bij omlaag bewegen hoort een
negatieve snelheid.
Hiernaast zie je hoe de snelheid van de bal tijdens
de beweging verandert. De rechte lijn is de raaklijn aan de kromme op t = 1,0 s.
A
Met welke snelheid werd de bal omhoog gegooid?
B
Wanneer beweegt de bal versneld, wanneer vertraagden wanneer is deze in ‘t hoogste punt?
C
Bereken de versnelling die de bal dan ondervindt.
D
Leg uit hoe je aan de figuur kunt zien dat de bal luchtwrijving ondervindt.
E
Bepaal met behulp van de figuur de maximale hoogte van de bal.
II
WINDKRACHT (trad)
De windkracht kan worden gemeten door de wind tegen een
plank te laten blazen die is opgehangen aan een koord. De
plank heeft een massa van 200 gram.
A
Teken hiernaast op schaal de krachten die op de plank
werken (teken alle krachten in Z!). Hint: parallellogram!
B
Bepaal de grootte van die krachten uit je constructie.
C
Bereken de grootte van de krachten met goniometrische
formules.
III OPTREKKEN MET CONSTANTE KRACHT (trad)
Een auto met massa van 890 kg begint op t = 0
te rijden. De motorkracht is constant 1,00 kN.
De auto ondervindt een constante rolwrijving en
luchtwrijving. In de figuur hieronder is het v,tdiagram van de beweging gegeven.
A
Hoe kan je aan de grafiek zien dat er ook
luchtwrijving was?
B
Bepaal in de grafiek hiernaast de versnelling op tijdstip t = 0.
C
Bereken de rolwrijvingskracht.
De luchtwrijving kan je berekenen met de formule, Flucht=kv2, hierin is k een constante.
D
Toon aan dat de eenheid van k = kg/m is.
E
Bepaal de getalswaarde van k (neem aan dat op tijdstip t =100 de snelheid constant is).
F
Bereken op twee verschillende manieren de versnelling als de snelheid 20 m/s is.
BLOK 4
A
MECHANICA
2
DE TESTRIT (trad)
Met een auto is op een horizontale weg ‘n
testrit gemaakt. In de grafiek hiernaast zie
je de gegevens van deze rit. Volgens specificaties uit de folder kan de auto in 10 s van
0 tot 80 km/h versnellen.
A
Laat met een berekening zien of daar
aan voldaan is.
In de grafiek zitten 3 dalende stukjes omdat de chauffeur dan net even schakelt. Na het schakelen
versnelt de auto weer. De auto heeft een massa van 1,2x 103 kg. Er is geen rolwrijving.
B
Bereken de versnelling van de auto in zijn 2 en 3, dus rond de 10 en rond de 20 m/s.
C
Bepaal met behulp van de grafiek de motorkracht in de periode van t = 0 tot 2,0 s.
D
Bereken uit je antwoorden bij B en bij C de luchtwrijving bij 10 en bij 20 m/s.
E
Geldt hier de regel dat bij dubbele snelheid de luchtwrijving inderdaad 4x zo groot wordt?
B
SLEPENDE KWESTIES (trad)
Een massa M van 100 gram wordt met een touw met constante snelheid
voortbewogen. Er is een forse luchtwrijving omdat Roos met haar Föhn
tegen de bewegingsrichting in blaast. De massa rust niet op de bodem. De
hoek tussen touw en de verticaal is hiernaast op te meten.
A
Teken hiernaast op schaal de krachten die er op M werken.
B
Bereken de grootte van luchtwrijving die Roos’ föhn oplevert en
bereken ook de grootte van de andere krachten die er op M werken.
Even later wordt de massa met weer door de lucht voortgetrokken, nu is
de hellingshoek veel groter (weer meten!). De massa beweegt versneld,
omdat er geen wrijving meer is (Roos föhn is kapot gegaan). Ook hier is
geen normaalkracht van de bodem op de massa van 100 gram
C
Teken hiernaast de krachten die er nu op de massa werken.
D
Bereken hun grootte.
E
Bereken de versnelling van deze massa.
C
DE JOJO (HAVO 1985)
In de figuur hiernaast zie je een jojo. Deze jojo bestaat uit 2 cirkel
vormige helften, verbonden door een as. Hieraan is een dun touw
bevestigd van 93 cm lengte. We wikkelen het touwtje - op 3,0 cm na
– geheel om de as. Aan het einde van het touwtje zit een lusje waar
een vinger door kan worden gestoken. De jojo wordt nu losgelaten.
Het touwt wikkelt zich af tot de jojo bij het laagste punt komt,
waarna deze weer omhoog klimt in het touw. Na ‘t bereiken van dit
hoogste punt gaat bij weer dalen. Dit op & neer bewegen herhaalt
enkele keren. Om de draairichting te kunnen volgen, brengen we op
de zijkant van de jojo een pijl aan. Als we de jojo los laten, draait hij
in de richting van de pijl.
A
Beredeneer in welke richting de jojo draait als hij vanuit het laagste punt van het touw voor
de eerste keer omhoog klimt.
3
BLOK 4 MECHANICA
Tijdens het omlaag gaan zijn er tegelijkertijd 2 bewegingen te onderscheiden:
(1) de draaiende beweging om de as (rotatie)
(2) een verplaatsing langs een rechte, verticale lijn (translatie).
We meten de tijd die de jojo gemiddeld nodig heeft om, ná te zijn losgelaten, een afstand af te
leggen van respectievelijk 10 , 20 , 40 , 60 en 80 cm (zie tabel).
Afstand (cm)
tijd (sec)
10
0,48
20
0,68
40
0,97
60
1.18
80
1,37
B Bepaal met behulp van deze tabel of de translatie eenparig versneld is .
De translatiesnelheid (m/s) waarmee de jojo - na het loslaten – omlaag beweegt, is als functie van
de tijd weergegeven in de figuur hierboven. Een negatieve snelheid betekent dat de snelheid
omlaag gericht is.
C
Bepaal met deze figuur hoe lang het duurt totdat de jojo voor de eerste keer zijn laagste punt
bereikt.
D
Bepaal met de figuur de versnelling van de jojo in het laagste punt.
E
Bereken daaruit de kracht die het touwtje dan op de draagvinger uitoefent.
D
TREIN IN HET WEB (HAVO 2015-2)
In de film Spiderman 2 stopt de held Spiderman een op hol
geslagen trein met draden gesponnen uit spinrag. Engelse
natuurkunde studenten van de Universiteit van Leicester
hebben berekend of het spinrag van een spin hiervoor
sterk genoeg is. In deze opgave gaan we deze berekening
in stappen na.
De studenten veronderstelden dat een trein zonder spinnendraden eenparig vertraagd tot
stilstand komt. De trein in de film heeft een beginsnelheid van 25 m/s en wordt in 50 s tot
stilstand gebracht. De massa van de trein met inzittenden is 2,0·105 kg.
A
Bereken de remafstand van de trein.
B
Bereken de resulterende kracht die nodig is om de trein af te remmen.
BLOK 4
MECHANICA
4
In de film gebruikt Spiderman draden van spinrag
die hij links en rechts van de trein aan de gebouwen
vast schiet. De eerste draden die Spiderman aan de
gebouwen bevestigd heeft, maken een hoek α met
de trein. Zie figuur, deze is niet op schaal. Tijdens
het afremmen verandert hoek α en worden de
draden langer. De resulterende kracht F op de trein
wordt hierdoor groter.
C
Leg uit waarom de resulterende kracht F bij
het remmen groter wordt als:
* hoek α verandert,
* de draden (elastisch) langer worden.
De snelheid van de trein zal niet eenparig afnemen omdat de resulterende kracht groter wordt. In
de figuur hierboven staan drie (v,t)-grafieken, A, B en C.
D
Leg uit welke grafiek het snelheidsverloop van de trein tijdens het afremmen het beste
weergeeft.
Als de draden maximaal zijn uitgerekt, is de spankracht in de linkerdraad 1,8.105 N. De (relatieve)
rek van het spinrag van Spiderman is dan 40.Uit de film blijkt dat elk van de twee draden van het
spinrag van Spiderman bestaat uit acht losse draden. De diameter van een van deze acht draden is
5,0 mm. De diameter is tijdens het remmen constant. Het sterkste spinrag dat in de natuur wordt
gevonden, heeft een elasticiteitsmodulus van 12 GPa bij een (relatieve) rek van 40.
E
Leg met behulp van een berekening van de spanning uit of het spinrag dat in de natuur
wordt gevonden minder sterk is dan, even sterk is als, of sterker is dan het spinrag van Spiderman.
E
EEN SPRONG BIJ VOLLEYBAL (VWO 2015-1)
Bij volleybal springt een speler vaak uit stand recht omhoog. De verticale snelheid van het
zwaartepunt van een volleyballer tijdens de afzet en de daaropvolgende beweging los van de
grond is weergegeven in de grafiek hier onder. Tijdens de sprong zijn de ‘afzetkracht’ en de
zwaartekracht van belang. De afzetkracht is de kracht van de grond op de volleyballer tijdens de
afzet. We verwaarlozen in deze opgave de luchtweerstand.
5
BLOK 4 MECHANICA
De volleyballer heeft een massa van 75 kg.
A
Bepaal met behulp van de v,t-grafiek de maximale
afzetkracht op de volleyballer.
B
Bepaal met behulp van de v,t-grafiek het hoogteverschil
van het zwaartepunt van de volleyballer tussen het begin van
de afzet en het hoogste punt.
Bij de studie bewegingswetenschappen wordt zo’n verticale sprong bestudeerd. Daarbij wordt een
computermodel gebruikt van een andere sprong dan de eerdere sprong. Een sprong bestaat uit
een afzet en een beweging los van de grond. Drie momenten van een sprong staan in de figuur
hieronder weergegeven. De figuur is niet op schaal
* In positie A is de springer maximaal door zijn knieën gezakt. Dit is het begin van de sprong.
* In positie B komt de springer los van de grond.
* In positie C bevindt de springer zich in het hoogste punt.
Het afzetten wordt vergeleken met het ontspannen van een
gespannenveer. Daarbij geldt voor de grootte van de afzetkracht:
Fafzet = Cu = C( yB - y).
Hierin is: C de veerconstante, u de uitwijking vanaf de evenwichtsstand, y de hoogte van het zwaartepunt boven de grond en yB de
hoogte van het zwaartepunt op het moment dat de springer los
komt van de grond.
Hiernaast staat het computermodel als serie
vergelijkingen. In elk model zijn drie regels opengelaten.
Het model moet aan de volgende eisen voldoen:
 De afzetkracht wordt voor alle waarden van y
correct beschreven.
 Op het hoogste punt (positie C in figuur 3)
stopt het model.
Figuur 4a en figuur 4b staan ook op de uitwerkbijlage.
C
Vul het model zo aan dat aan de eisen wordt
voldaan.
Een wetenschapper wil het model uitbreiden
om ook de energieën van een springer tijdens
zijn sprong te beschrijven. Hierbij wordt de
beschikbare energie tijdens de afzet, Eafzet,
vergeleken met de energie in een gespannen
veer.
D
Welke formule voor de afzetenergie Eafzet
moet de wetenschapper hiervoor aan het model
toevoegen? Gebruik hiervoor de grootheden uit
het model.
In het diagram hiernaast zijn de resultaten van
het uitgebreide model van de afzetenergie
tegen de tijd weergegeven.
E
Bepaal met behulp van deze figuur op de
op welk tijdstip het vermogen van de springer
maximaal is.
BLOK 4
MECHANICA
6
Hiernaast zijn in een diagram de zwaarte-energie en de
afzetenergie van de springer weergegeven.
F
Voer de volgende opdrachten uit:

Bepaal in dit diagram de grootte van de kinetische
energie op t = 0,18 s.

Teken in dit diagram het verloop van de kinetische
energie tegen de tijd.
F
SPRINT (VWO 2013-1 PILOT)
Kimberley en Jenneke maken met behulp van een video-opname een(s,t)-diagram van een sprint
van Carl Lewis over 100 meter, zie rechtsboven. Over het deel van de race vanaf t = 4,0 s trekken
Kimberley en Jenneke de volgende conclusies:
 Vanaf t = 4,0 s is de snelheid van Lewis constant.
 Deze snelheid is gelijk aan 11,7 m/s.
A
Laat met behulp van het s,t-diagram zien dat beide conclusies juist zijn.
Kimberley en Jenneke onderzoeken nu het begin van de race. Ze hebben elk een hypothese over
de eerste 4 seconde.
Kimberley Hypothese 1 “Lewis leverde in de eerste 4 s een constante kracht.”
Jenneke Hypothese 2 “Lewis leverde in de eerste 4 s een constant vermogen.”
In het (v,t)-diagram hiernaast staat gegeven hoe de snelheid zou
verlopen als hypothese 1 van Kimberley klopt, uitgaande van de
snelheid op t = 4,0 s. De massa van Carl Lewis bedraagt 80 kg.
B
Bepaal de grootte van de kracht die Kimberley in haar model
heeft gebruikt.
Neem aan dat de wrijvingskrachten verwaarloosd mogen worden.
C
Laat zien dat het v,t-diagram hiernaast en het s,t-diagram
hier boven niet met elkaar in overeenstemming zijn.
7
BLOK 4 MECHANICA
Hypothese 1 van Kimberley blijkt dus niet te kloppen. Jenneke werkt nu
hypothese 2 uit. Zij maakt een model waarin het geleverde constante
vermogen alleen gebruikt wordt voor toename van de kinetische
energie. Het (v,t)-diagram dat uit dit model volgt, is hiernaast
weergegeven. De snelheid voldoet aan de formule:
v(t) = k √t
(1)
Hierin is k een constante.
D
Leid de formule af gebruikmakend van formules uit BINAS.
Jenneke wil onderzoeken of hypothese 2 het verloop van de afgelegde afstand in de eerste 4 sec
juist beschrijft. Daarvoor maakt ze in Excel een trendlijn door het begin van de (s,t)-grafiek van het
eerste s,t-diagram hierboven (naast de foto van Carl Lewis). Ze krijgt dan een lijn door de meetpunten die voldoet aan de formule:
s (t) = 3,9. t1,5
(2)
Haar leraar legt uit dat de snelheidsfunctie de afgeleide is van de plaats functie en schrijft op hoe
die afgeleide bepaald moet worden.
E
Voer de volgende opdrachten uit om te controleren of hypothese 2 klopt:
*
Bereken de waarde van k zodat formule (1) klopt met de snelheid op t = 4,0 s.
*
Toon aan dat deze waarde van k overeenkomt met formule (2).
*
Toon aan dat de exponent in formule (2) klopt.
*
Bepaal de grootte van het constante vermogen van Carl Lewis in de eerste 4 seconde.
G TREKKERTREK (VWO 2013-2 PILOT)
Bij trekkertrek (ook wel tractor pulling genoemd) moet een
tractor een sleepwagen voorttrekken die opzettelijk een grote
wrijvingskracht ondervindt: de voorkant van de wagen heeft
geen wielen, maar sleept over de grond. Tijdens het rijden
schuift een zwaar ballastblok op de sleepwagen naar voren. Zo
neemt de wrijvingskracht toe, waardoor de tractor met
sleepwagen afgeremd wordt en tot stilstand komt.
Het doel van trekkertrek is om een zo groot mogelijke
afstand af te leggen. Als deze afstand 100 m of meer is, is er
sprake van een ‘full pull’. Hiernaast het (v,t)-diagram van een
deelnemer.
A
Ga met het v,t-diagram na of deze poging een ‘full pull’
opleverde.
BLOK 4
MECHANICA
8
De tractor en de sleepwagen zijn hierboven
schematisch getekend. Daarbij zijn de massa’s van de
tractor, de sleepwagen en het ballastblok vermeld. De
massa is uitgedrukt in ton. In de grafiek hieronder
verloop van de wrijvingskracht op de sleepwagen
weergegeven als de wagen de volledige afstand van
100 m zou afleggen (‘full pull’). De bestuurder moet
erop letten dat de achterwielen van de tractor niet
gaan ‘spinnen’. Daarbij draaien de wielen snel rond en
vliegt veel zand weg. Dat gebeurt als de motor té veel
kracht op de wielen uitoefent.
Een vuistregel voor de optimale trekkracht die
de tractor zou moeten leveren is: ‘De trekkracht is
gelijk aan het eigen gewicht (in Newton) van de
tractor.’
B
Ga na of de trekkracht van de tractor tijdens de eerste paar seconden aan de vuistregel
voldoet. Bepaal hiertoe de trekkracht bij de start.
Jelle en Tjerk discussiëren over het spinnen. Jelle zegt dat bij spinnen de wielen geen grip hebben
op de grond, waardoor de bodem minder kracht op de wielen uitoefent. Tjerk zegt, dat (daardoor)
bij spinnen de derde Wet van Newton niet geldt.
C
Leg voor beide uitspraken uit of ze juist zijn.
De wedstrijden worden ingedeeld in gewichtsklassen.
In het reglement van een trekkertrekvereniging staat
nevenstaande tabel. Een tractor die lichter is dan de
gewichtsgrens, mag door ballast zwaarder gemaakt
worden tot het maximale gewicht.
D
Geef één voordeel en één nadeel van het
zwaarder maken van de tractor.
E
Geef aan of uit de tabel blijkt dat er een recht
evenredig verband bestaat tussen het maximale
gewicht en het maximale vermogen van de trekkers.
Tjerk zegt dat de oppervlakte onder de F,s-grafiek altijd gelijk is aan de arbeid die de tractor
verricht als hij een ‘full pull’ haalt.
F
Leg uit of Tjerk gelijk heeft.