Richtingscoëfficiënt

Richtingscoëfficiënt, differentiequotiënt, raaklijnen en de
afgeleide functie
Richtingscoëfficiënt
Binnen de Analyse speelt de richtingscoëfficiënt een belangrijke rol. Dat begint al bij lijnen.
Bij de vergelijking van lijn l : y  ax  b is het getal a de richtingscoëfficiënt van de lijn.
Dit getal zegt iets over hoe steil de lijn loopt: 1 stapje naar rechts betekent a stapjes
omhoog.
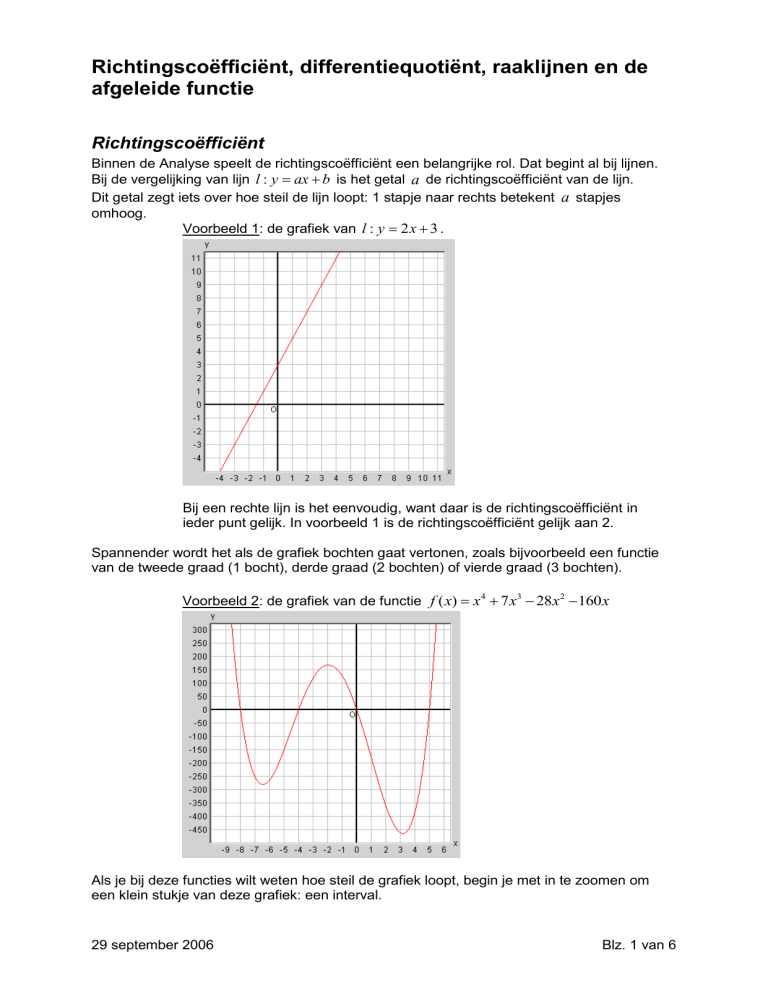
Voorbeeld 1: de grafiek van l : y  2 x  3 .
Bij een rechte lijn is het eenvoudig, want daar is de richtingscoëfficiënt in
ieder punt gelijk. In voorbeeld 1 is de richtingscoëfficiënt gelijk aan 2.
Spannender wordt het als de grafiek bochten gaat vertonen, zoals bijvoorbeeld een functie
van de tweede graad (1 bocht), derde graad (2 bochten) of vierde graad (3 bochten).
Voorbeeld 2: de grafiek van de functie f ( x)  x 4  7 x3  28x 2  160 x
Als je bij deze functies wilt weten hoe steil de grafiek loopt, begin je met in te zoomen om
een klein stukje van deze grafiek: een interval.
29 september 2006
Blz. 1 van 6
Richtingscoëfficiënt, differentiequotiënt, raaklijnen en de
afgeleide functie
Differentiequotiënt
Het differentiequotiënt is de gemiddelde stijging op een bepaald interval.
Een interval noteren we altijd als het stukje op de x -as waar we het over hebben.
Het interval [2,4] betekent dus het stukje grafiek dat begint bij x = 2 en eindigt bij x = 4.
Als we het meest linkse punt A noemen en het meest rechtse punt B, dan berekenen we
de gemiddelde stijging met:
verschil in y -waarde
y -waarde punt B  y -waarde punt A

verschil in x-waarde
x-waarde punt B  x-waarde punt A
of, in een formule:
y  yA
y
 B
x
xB  x A
Hoe doe je dit in een opgave?
1. In de opgave zijn twee punten gegeven met hun coördinaten.
Dit zijn de punten A en B in bovenstaande formule, waarbij A het meest linkse punt is.
2. Soms is alleen een interval gegeven, zoals [2, 4]. Noem dan het meest linkse punt A.
Je weet nu de x -waarde van A. Reken de y -waarde uit door de x -waarde in te
vullen in het functievoorschrift.
Doe hetzelfde met het meest rechtse punt, punt B.
Zie eventueel het document “functies plotten op de TI-83” hoe je met behulp van de
GR een y -waarde uit kunt rekenen.
3. Vul nu de x -waarden en y -waarden van A en B in in
yB  y A
y
en reken zo
uit.
x
xB  x A
Hoe herken je in de opgave dat je een differentiequotiënt moet uitrekenen?
a. Gemiddelde stijging/daling op een (tijds)interval, bijvoorbeeld:
“Bereken hoeveel het aantal … is toegenomen op de 9e dag”.
Als t = 0 het begin is van de 1e dag, dan begint 9e dag bij t = 8 en is afgelopen bij t = 9.
b. Gemiddelde snelheid gedurende een tijdsinterval.
c. De richtingscoëfficiënt van de lijn die door twee punten (A en B) van een grafiek loopt.
29 september 2006
Blz. 2 van 6
Richtingscoëfficiënt, differentiequotiënt, raaklijnen en de
afgeleide functie
Voorbeeld 3
Gegeven is de functie f ( x)  x 4  7 x3  28x 2  160 x .
a. Bereken de gemiddelde verandering op het interval [2,4].
b. Bereken de vergelijking van de lijn door de punten xA  2 en xB  4 .
Uitwerking a.
Stap 1 en 2:
Het meest linkse punt A heeft een x -waarde van 2. Invoeren van de functie in
de GR en raadplegen van de tabel levert een y -waarde van 360 .
Het meeste rechtse punt B heeft een x -waarde van 4. In de tabel staat hierbij
een y -waarde van 384 .
Stap 3:
Invullen in
yB  y A
384  (360) 24

 12 . Let op de mintekens!
levert
42
2
xB  x A
Uitwerking b.
We weten nu dat de lijn door A en B een richtingscoëfficiënt heeft van 12 .
Ieder stapje naar rechts ga je immers 12 omlaag.
Stel dat de lijn door A en B de volgende vergelijking heeft: l : y  ax  b . Dan
kunnen we bij a de richtingscoëfficiënt invullen en krijgen we y  12 x  b .
We weten ook dat deze lijn door punt A gaat, dus coördinaat
( x, y )  (2,  360) ligt op deze lijn. Als we dit ook invullen krijgen we:
360  12  2  b . Nu kunnen we eenvoudig het getal b uitrekenen: het getal
waar deze lijn de y -as snijdt. Immers 384  24  b , dus 336  b .
Nu is het plaatje compleet. We weten de getallen a en b dus :
l : y  12 x  336 is de vergelijking van de lijn door punten A en B.
In dit plaatje is de lijn door de punt A en B ingetekend.
29 september 2006
Blz. 3 van 6
Richtingscoëfficiënt, differentiequotiënt, raaklijnen en de
afgeleide functie
Raakpunten en raaklijnen
Soms zijn we niet geïnteresseerd in de gemiddelde snelheid op een bepaald tijdsinterval,
maar willen we de snelheid op een bepaald moment weten. We maken nu het tijdsinterval
zo klein mogelijk, zodat de grafiek ons niet meer kan ontsnappen, bijvoorbeeld
 xA  0.001 , xA  0.001 . We krijgen zo een goede benadering van de richtingscoëfficiënt
in het punt A. Om ons veel rekenwerk te besparen, heeft de TI-83 hiervoor een standaard
functie: Calc, optie 6: dy/dx.
Voorbeeld 4
Gegeven is weer de functie f ( x)  x 4  7 x3  28x 2  160 x .
Bepaal nu de richtingscoëfficiënt in punt A.
Uitwerking
Ga naar de grafiek en kies Calc, optie 6: dy/dx. Typ in: 2 en druk op ENTER.
De GR geeft als antwoord: dy/dx = 156 . We mogen aannemen dat dit zeer dicht in de
buurt ligt van de werkelijke richtingscoëfficiënt in punt A.
We kunnen nu ook een raaklijn gaan tekenen die de grafiek in het punt A raakt. Deze lijn
heeft dezelfde richtingscoëfficiënt als de grafiek bij punt A en gaat bovendien door punt A.
Ook van deze raaklijn kunnen we de vergelijking opstellen. Dit werkt op dezelfde manier als
bij voorbeeld 3b. We kunnen onze berekening gelukkig weer controleren met de GR met
behulp van DRAW, optie Tangent. De toets DRAW zit boven de PGRM-toets.
Voorbeeld 5
a. Bereken algebraïsch de vergelijking van de raaklijn in punt A.
b. Teken de raaklijn op de GR.
Uitwerking a.
Bij opgave 4 hebben we gevonden dat de richtingscoëfficiënt in punt A is gelijk aan
156 . Als we dit invullen in de algemene vergelijking van een lijn l : y  ax  b krijgen
we y  156 x  b . Deze raaklijn gaat door het punt A, dus ( x, y )  (2,  360) ligt op
deze lijn. Invullen levert: 360  156  2  b , b = 48 .
De vergelijking van de raaklijn wordt dan y  156 x  48
29 september 2006
Blz. 4 van 6
Richtingscoëfficiënt, differentiequotiënt, raaklijnen en de
afgeleide functie
Uitwerking b.
Om te controleren of onze berekening klopt, kunnen we twee dingen doen:
1. De vergelijking van de raaklijn invullen bij Y2 en plotten. Als het goed is, raakt
deze lijn de grafiek inderdaad alleen bij punt A.
2. De raaklijn in punt A laten tekenen door de GR met behulp van DRAW, optie
Tangent. Voer de x -waarde in (in dit geval 2) en druk op ENTER. De GR tekent nu
de raaklijn en geeft onderin beeld een schatting van de vergelijking van deze raaklijn.
Afgeleide functie
Als je in een auto zit en je kijkt een tijdje naar de kilometerteller, krijg je een aardig beeld van
hoe hard iemand rijdt. Zo heb ik zelf een keer een lift gehad van Utrecht naar Amersfoort
over de oude weg waar je 80 mocht rijden, die bestond uit twee te brede rijstroken. Op die
weg was in het midden voldoende ruimte voor waaghalzen om in te halen. Ik zat naast een
Griek, helemaal in het wit gekleed, die kennelijk zijn rijbewijs wilde bewijzen. Hij zette zijn
teller op 150 km/uur en daagde iedere tegenligger uit om net iets eerder in te voegen dan hij
dat deed. Ik heb heel wat schietgebedjes gedaan in die auto…
Als je nu links een grafiek maakt van de afgelegde kilometers tegen de tijd, dan zie je dat die
aardig steil loopt. Dat klopt ook, want de snelheid was in die 15 minuten behoorlijk hoog.
Als we vervolgens rechts een grafiek tekenen van de snelheid, dan zien we bovendien dat er
venijnige dippen in zitten, namelijk de momenten dat mijn Griekse chauffeur even bot op de
rem moest voor een tegenligger om daarna weer vrolijk vol gas te geven.
Verticaal: afgelegde afstand in km.
Horizontale as: tijd in min.
Verticale: snelheid in km/uur
Horizontale as: tijd in min.
De grafiek van de snelheid in km/uur is de grafiek die precies aangeeft hoe hard er
op ieder moment tijdens dat kwartier werd gereden. Je zou kunnen zeggen: bij ieder punt in
de linker grafiek is de afgeleide (dy/dx) bepaald en hiervan is rechts een grafiek getekend.
De rechter grafiek noemen we dan ook de grafiek van de afgeleide. Je ziet dat die grafiek
van de afgeleide ons soms meer informatie geeft dan de grafiek van de functie zelf!
Als we het functievoorschrift kennen van de functie zelf, dan kunnen we volgens een aantal
regels die op jullie formulekaart staan de afgeleide functie bepalen. Dat is mooi, want daar
kunnen we een aantal leuke dingen mee doen.
29 september 2006
Blz. 5 van 6
Richtingscoëfficiënt, differentiequotiënt, raaklijnen en de
afgeleide functie
Om te beginnen kunnen we die afgeleide functie invoeren bij bijvoorbeeld Y2 en plotten op
de GR. Wat dan opvalt is dat, als de grafiek van originele functie even horizontaal loopt, de
grafiek van de afgeleide functie even nul is. Kijk maar in de tekeningetjes hierboven:
op de momenten dat ik in- en uitstapte, liep de linkergrafiek even horizontaal, terwijl de
rechtergrafiek door nul gaat. Hier kunnen we handig gebruik van maken als we algebraïsch
een minimum of maximum willen berekenen van een grafiek.
Voorbeeld 6
Gegeven is de functie f ( x)  x 2  6 x  4 . Bereken algebraïsch het minimum.
Uitwerking
We hebben onze GR niet voor niets, dus eerst maar eens de grafiek van deze functie
bekijken en met de GR inschatten waar het minimum ongeveer moet liggen.
Bij mij levert dit x  3, 0000009 op en y  5 . Maar ja, wat is het nu precies?
De regels toepassen levert als afgeleide functie f '( x)  2 x  6 . Deze afgeleide is nul
als 2 x  6  0 , dus als x  3 . De y -waarde in dit punt is inderdaad 32  6  3  4  5 .
In dit geval kunnen we de grafiek van de afgeleide berekenen en vervolgens plotten.
We zien inderdaad dat de grafiek van y  2 x  6 bij x  3 door de x -as gaat.
Soms echter zijn de functies zo ingewikkeld, dat we daar niet één, twee, drie een afgeleide
functie van kunnen berekenen. In die gevallen kunnen we de opgave toch oplossen met
behulp van een grafische benadering met de GR. Daarbij maken we gebruik van de functie
nDerive in het menu Math, Math, optie 8.
Voorbeeld 7
Gegeven is de functie f ( x ) 
15 ^ (ln x)
.
x 2  15
Bepaal punt(en) waarbij deze functie een richtingscoëfficiënt heeft van 1 .
Uitwerking
Voer het functievoorschrift in bij Y1.
Voer bij Y2 in: nDerive(Y1,X,X).
De functie Y1 kun je selecteren via VARS, Y-VARS, Function.
Plot de grafieken in het standaard window.
Je ziet nu dat grafiek 2 als het ware een trechter naar beneden vormt en 2x langs de
y -waarde 1 komt.
Plot bij Y3 een horizontale lijn bij y = 1 . Bepaal met Calc, Intersect de snijpunten
van Y2 en Y3. Let op: kies de juiste grafieken bij First Curve en Second Curve.
Je vindt nu de x -waarden waarvoor geldt dat de richtingscoëfficiënt gelijk is aan 1 .
Door deze x -waarden in te vullen in het originele functievoorschrift, kun je de
bijbehorende y -waarden uitrekenen. Of: ga met de pijltjestoets omhoog naar de
grafiek van Y1 en lees de y -waarde af bij iedere gevonden x -waarde.
Ik kom uit op: (1,97; -0,58) en (5,78; 6,28).
Veel plezier met de fantastische mogelijkheden van de GR!
29 september 2006
Blz. 6 van 6