Bijlage Krachten
2.5
Eurek(h)a!1
p. 169e
Meerdere krachten op een voorwerp
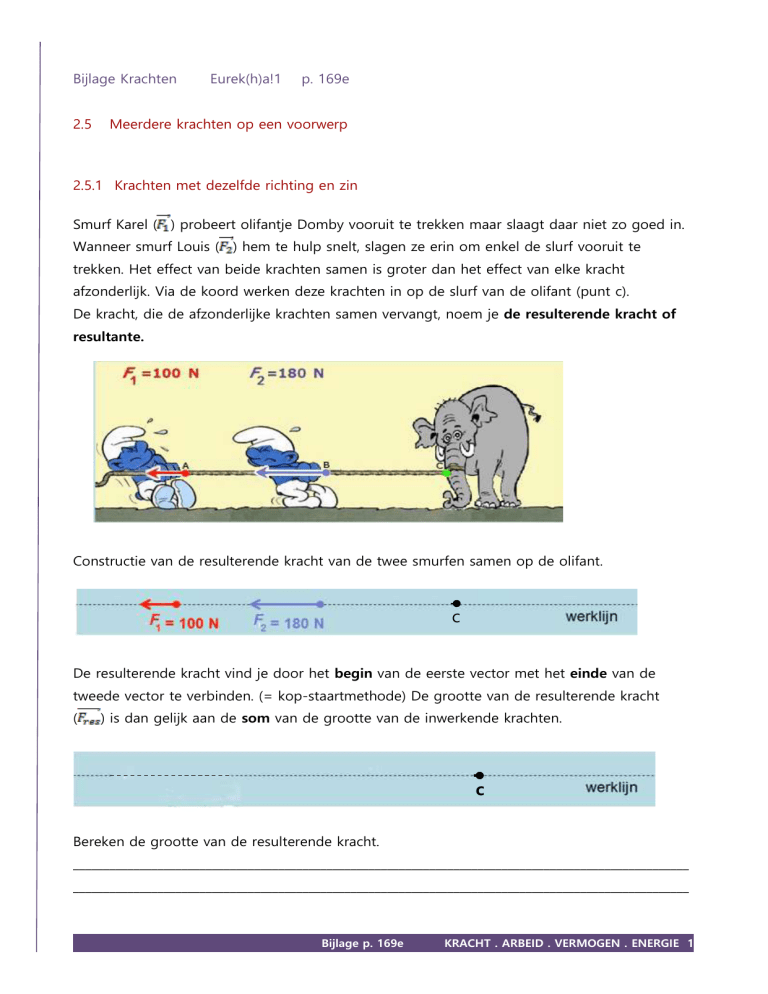
2.5.1 Krachten met dezelfde richting en zin
Smurf Karel ( ) probeert olifantje Domby vooruit te trekken maar slaagt daar niet zo goed in.
Wanneer smurf Louis ( ) hem te hulp snelt, slagen ze erin om enkel de slurf vooruit te
trekken. Het effect van beide krachten samen is groter dan het effect van elke kracht
afzonderlijk. Via de koord werken deze krachten in op de slurf van de olifant (punt c).
De kracht, die de afzonderlijke krachten samen vervangt, noem je de resulterende kracht of
resultante.
c
Constructie van de resulterende kracht van de twee smurfen samen op de olifant.
c
De resulterende kracht vind je door het begin van de eerste vector met het einde van de
tweede vector te verbinden. (= kop-staartmethode) De grootte van de resulterende kracht
(
) is dan gelijk aan de som van de grootte van de inwerkende krachten.
c
Bereken de grootte van de resulterende kracht.
______________________________________________________________________________________________________
______________________________________________________________________________________________________
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 1
2.5.2 Krachten met dezelfde richting en tegengestelde zin
Smurf Louis ( ) verwijt smurf Karel ( ) dat hij niet hard genoeg aan het touw trekt. Ze doen
aan touwtje trek. Beiden oefenen een kracht uit in dezelfde richting maar in tegengestelde
zin. De resulterende kracht is nu kleiner.
Constructie van de resulterende kracht in het punt c.
c
De resulterende kracht vind je weer door het begin van de eerste vector met het einde van de
tweede vector te verbinden. De grootte van de resulterende kracht (
) is gelijk aan het
verschil van de grootte van de inwerkende krachten.
c
Bereken de grootte van de resulterende kracht.
______________________________________________________________________________________________________
______________________________________________________________________________________________________
2
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
Samengevat
De resulterende kracht (
) vervangt alle krachten die op een voorwerp inwerken en heeft
hetzelfde effect als alle krachten samen.
Krachten met dezelfde richting en dezelfde zin versterken elkaar. De resulterende kracht
heeft dezelfde richting en zin als de inwerkende krachten. De grootte van de resulterende
kracht is gelijk aan de som van de grootte van de inwerkende krachten.
Krachten met dezelfde richting maar met een tegengestelde zin werken elkaar tegen. De
richting van de resulterende kracht is dezelfde als de inwerkende krachten, de zin valt samen
met die van de grootste inwerkende kracht. De grootte van de resulterende kracht is gelijk
aan het verschil van de grootte van de inwerkende krachten.
Opmerking
Wanneer twee even grote krachten, met dezelfde werklijn en in tegengestelde zin, op
eenzelfde vast lichaam inwerken, dan is de resulterende kracht gelijk aan nul.
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 3
2.6
Oefeningen
1 Twee honden vechten om een been. Op onderstaande
figuur zie je in bovenaanzicht de richting en de plaats
waarop ze kracht uitoefenen op het bot.
Teken op iedere figuur de resulterende kracht in het
massapunt.
2 De kraan tilt een voorwerp omhoog met een kracht (
van 2 500 N. De zwaartekracht (
)
, uitgeoefend door het
aardoppervlak op het voorwerp, is reeds getekend.
Teken
en de resulterende kracht (
) op het voorwerp.
(schaal: 1 cm = 1 000N)
Hoe groot is de resulterende kracht? __________________________________________________________
Welk gevolg heeft de resulterende kracht voor het voorwerp?
___________________________________________________________________________________________________
4
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
+3
BEWEGING EN KRACHTEN
+3.1 Rust en beweging
Overal om je heen is beweging merkbaar: een auto die voorbij rijdt, een kind op de fiets, een
bal die naar beneden valt, eb en vloed, de zon die schijnbaar om de aarde draait ....
Bomen en huizen lijken in rust, een koppeltje dat rustig op een bankje zit te praten lijkt in rust.
Maar is dat ook zo?
Bekijk jezelf thuis, rustig in de zetel liggend voor de televisie. Ten opzichte van de televisie en
je woonkamer ben je in rust en toch beweeg je met een snelheid van meer dan 1 000 km/h
rond de as van de aarde.
De passagiers zijn ten opzichte van het vliegtuig in ________________
Hun snelheid bedraagt __________________
De passagiers en het vliegtuig zijn
ten opzichte van jou op het
aardoppervlak in _____________________
Hun snelheid bedraagt ______________
Samengevat
Rust en beweging, maar ook snelheid zijn relatief. We moeten een 'referentiestelsel'
afspreken ten opzichte waarvan we de verplaatsing bekijken.
Een bewegend voorwerp verplaatst zich volgens een bepaalde baan. Een vlinder volgt een
willekeurige baan tussen de bloeiende bloemen in de tuin. Een formatie stuntvliegers laat
kromlijnige condensatiestrepen achter in de lucht. Wanneer je de lift neemt, volg je een
rechtlijnige baan. In een draaimolen op de kermis beschrijf je een cirkelvormige baan.
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 5
Samengevat
Een beweging kan gebeuren langs een rechtlijnige of een kromlijnige baan.
Bij een kromlijnige baan kan je een onderscheid maken tussen een willekeurige en
cirkelvormige baan.
+3.2 Snelheid
Janne fietst naar school. Ze vertrekt om 7 h 50 min.
Om 8 h 20 min. arriveert Janne aan school.
Ze heeft daarbij een afstand afgelegd van 7,5 km.
Tijdens een beweging loopt de tijd. Er is dus steeds een
verandering van het tijdstip. Een tijdstip wordt weergegeven
met de letter t.
Hoe lang heeft Janne er over gedaan om naar school te fietsen? _______________________________
We spreken van een tijdsduur t.
t = te - tb (eindtijdstip - begintijdstip)
De gemiddelde snelheid (v ) waarmee Janne naar school fietste kan je berekenen door de
afgelegde weg (s) te delen door de tijdsduur.
Formule:
Eenheid:
Bereken nu de snelheid waarmee Janne naar school fietste.
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
Bereken ook eens hoeveel m/s dit is.
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
6
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
dus:
________
m/s
km/h
________
Samengevat
De snelheid van een voorwerp is de verhouding van de afgelegde weg tot de tijdsduur van
de beweging.
+3.2.1
Snelheid in een grafiek
Een voorwerp beweegt zoals weergegeven in volgende grafiek.
s (m)
t (s)
t (s)
0
(m
Hoe groot is de gemiddelde snelheid van het voorwerp gedurende de eerste 4 s?
)
Bereken______________________________________________________________________________________________
______________________________________________________________________________________________________
Hoe groot is de snelheid gedurende de 6 daarop volgende s?
Bereken______________________________________________________________________________________________
______________________________________________________________________________________________________
Hoe kun je in de grafiek zien dat een voorwerp sneller beweegt?
______________________________________________________________________________________________________
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 7
Samengevat
De helling van de rechte is een maat voor de snelheid van het voorwerp. Hoe sneller het
voorwerp beweegt, hoe steiler de helling.
+3.2.2 Oefeningen
1 Anneke zit op de achterbank van de wagen en maakt de
opmerking: 'Papa, je mag hier niet sneller rijden dan 30 m/s.'
Heeft Anneke gelijk?
Gegeven:
Gevraagd:
Oplossing:
Antwoord:
2 Een wielrenner haalt bij een afdaling een snelheid van 72 km/h. Hoeveel m/s is dat?
___________________________________________________________________________________________________
___________________________________________________________________________________________________
3 Een auto is 100 m van je verwijderd en rijdt met een snelheid van 55 km/h. Is het verstandig
om nog de weg over te steken? Bereken hoeveel tijd je nog hebt.
Gegeven:
Gevraagd:
Oplossing:
Antwoord:
8
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
4a Je trouwe viervoeter Fifi is op pad langs een rechte baan. Hij loopt met een constante
snelheid van 3,6 m/s gedurende 25,0 s. Welke afstand heeft hij afgelegd?
Gegeven:
Gevraagd:
Oplossing:
Antwoord:
4b Hij slaat een zijpad in en loopt met dezelfde snelheid nog eens 360 m rechtdoor. Hoeveel
tijd heeft hij hiervoor nodig?
Gegeven:
Gevraagd:
Oplossing:
Antwoord:
4c Hij neemt opnieuw een zijpaadje en loopt gedurende nog eens 50,0 s tot hij bij een klein
heuveltje komt. Hier begint hij ijverig te graven. Wat is zijn snelheid tijdens dit laatste
stukje weg?
Gegeven:
Gevraagd:
Oplossing:
Antwoord:
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 9
+3.3 Eenparige rechtlijnige beweging
Experiment
Probleemstelling
Welke beweging maakt het wagentje?
Wat verwacht je?
Het wagentje beweegt volgens
□ een rechte baan met een veranderlijke snelheid;
□ een rechte baan met een constante snelheid;
□ een kromlijnige baan met een veranderlijke snelheid;
□ een kromlijnige baan met een constante snelheid.
Materiaal
speed buggy
chronometer / smartphone
rolmeter
krijt
Werkwijze
Zet op de vloer in je lokaal of gang om de meter een krijtlijn.
Start het wagentje ongeveer 1 m voor de eerste streep.
Start de chronometer wanneer het wagentje over de eerste streep rijdt.
Meet de tijd telkens als het wagentje over een volgende streep rijdt. Werk eventueel
met tussentijden die je op je smartphone kunt aflezen.
Noteer de resultaten in de tabel en voer de berekeningen uit.
Metingen
s (m)
t (s)
s (m)
t (s)
v = s/t (m/s)
0,0
0,0
-
-
-
1,0
2,0
3,0
4,0
5,0
10
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
Wat valt je op als je s en t in de tabel bekijkt?
______________________________________________________________________________________________________
Wat betekent dit?
______________________________________________________________________________________________________
Maak de s(t)- en v(t)-grafiek.
s(t)- grafiek
v(t)-grafiek
De s(t)- grafiek geeft het verband weer tussen de afstand (s) en de tijd (t). Het is ______________
______________________________________________________________________________________________________
De verhouding
is een____________________ namelijk____________________________________________
De v(t)-grafiek is een rechte______________________________________ met de tijdas.
De beweging is dus een eenparige rechtlijnige beweging of ERB.
Besluit
Een eenparige rechtlijnige beweging of ERB is een beweging van een voorwerp langs een
rechte baan met een constante snelheid.
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 11
+3.3.1 Oefeningen
1 Geef van de bewegende voorwerpen in de tabel met 'ja' of 'nee' aan of ze een rechte baan
volgen, een constante snelheid hebben of een ERB uitoefenen.
bewegend voorwerp
rechte baan
constante snelheid
ERB
een knikker die over een tafel rolt
een zwemmer die baantjes trekt
een schansspringer
een kind op een roltrap
een vliegtuig in volle vlucht
een luchtballon die opstijgt
een trein aan topsnelheid
2 Bestudeer het s(t)-diagram van een
s (km)
bestelwagen die pakjes aflevert aan
huis.
Tussen 9 h en 9 h 30 voert de
bestelwagen een eenparige beweging
uit. Welke afstand heeft de chauffeur
van de wagen afgelegd tijdens deze
9h
9 h 30
10 h
t (h)
beweging? ______________________________
Welke is zijn tijdsduur? _________________
Welke snelheid heeft de wagen tussen 9 h en 9 h 30? ________________________________________
Wat gebeurt er tussen 9 h 30 en 9 h 35? ______________________________________________________
Welke is de gemiddelde snelheid van de bestelwagen tussen 9 h 35 en 10 h?
___________________________________________________________________________________________________
___________________________________________________________________________________________________
___________________________________________________________________________________________________
12
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
3 Hiernaast is het (v,t)-diagram getekend van
een auto die eenparig beweegt met een
snelheid van 30 m/s.
Teken in hetzelfde assenstelsel het (v,t)diagram van een motorfiets die met een
half zo grote snelheid eenparig beweegt
tussen de tijdstippen 20 s en 40 s.
4 Hiernaast zie je het (v,t)- diagram van de
beweging van een racewagen op het circuit
van Zolder.
Vul in en omcirkel.
De eerste 5 s neemt de snelheid TOE / AF
van _________ km/h tot ___________ km/h.
Dat is een VERSNELDE / VERTRAAGDE
beweging. De volgende ______________ s
moet de wagen VERSNELLEN / VERTRAGEN
en neemt de snelheid TOE / AF van
______________km/h tot ______________km/h.
Dat is een VERSNELDE / VERTRAAGDE beweging.
Daarna volgt een VERSNELDE / VERTRAAGDE beweging. De snelheid neemt dan
TOE / AF
van________________ km/h tot _______________ km/h in een tijdsduur van _________ s.
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 13
5 Jasper en Dries fietsen naar school. Leid uit de grafieken af wie van hen de grootste
snelheid heeft? Motiveer je antwoord.
Jasper
Dries
___________________________________________________________________________________________________
___________________________________________________________________________________________________
___________________________________________________________________________________________________
+3.4 Snelheid als vector
Je bent op dropping met de jeugdbeweging. De leiders
laten jou en je vrienden achter midden in een heuvelachtig
bos. Je wordt ten laatste om 12 uur 's nachts terug verwacht
in het clublokaal. Een niet zo simpele opgave. Wat wil je
allemaal weten vooraleer je aan je verplaatsing begint?
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
Sommige grootheden worden niet alleen gekenmerkt door hun grootte maar ook door hun
richting en zin. Zulke grootheden noemen we ________________________________grootheden.
Verplaatsing en snelheid zijn zo'n vectoriële grootheden.
Net zoals een kracht wordt de snelheidsvector voorgesteld door een pijl, getekend in het
zwaartepunt van het voorwerp.
Symbool van de snelheidsvector:
14
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
snelheidsvector op een rechtlijnige baan
snelheidsvector op een kromlijnige baan
Op de foto vind je alle elementen terug van de snelheid die de reddingsboot bezit.
Vul in en kies uit: 40 km/h - horizontaal - naar rechts - zwaartepunt.
Het aangrijpingspunt is het_______________
_____________________________________________
De richting is______________________________
en wordt voorgesteld door de richting van de
pijl.
20 km/h
De zin is____________________________________en
wordt aangeduid door de pijlpunt.
De grootte is ___________________________en wordt voorgesteld door de lengte van de pijl en de
schaal.
Samengevat
Snelheid is een vectoriële grootheid en wordt gekenmerkt door:
-
een aangrijpingspunt (het zwaartepunt van het voorwerp);
-
een richting (de raaklijn aan de gevolgde baan);
-
een zin (de bewegingszin);
-
een grootte v (
).
+3.5 Snelheid als vector: voorbeelden
1 Teken op onderstaande foto's de snelheidsvectoren in het aangrijpingspunt (rode punt).
Hebben de snelheidsvectoren dezelfde grootte, richting, zin en aangrijpingspunt?
aangrijpingspunt: HETZELFDE / VERSCHILLEND
•
richting: DEZELFDE / VERSCHILLEND _______________________
•
zin: DEZELFDE / VERSCHILLEND ____________________________
grootte: EVEN GROOT / VERSCHILLEND
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 15
aangrijpingspunt: HETZELFDE / VERSCHILLEND
•
•
richting: DEZELFDE / VERSCHILLEND _____________________
• •
zin: DEZELFDE / VERSCHILLEND __________________________
grootte: EVEN GROOT / VERSCHILLEND
De auto haalt het stappende meisje in met
een snelheid die vier maal groter is.
aangrijpingspunt: HETZELFDE / VERSCHILLEND
richting: overal DEZELFDE / VERSCHILLEND _____________
_____________________________________________________________
zin: DEZELFDE / VERSCHILLEND ___________________________
_____________________________________________________________
grootte: overal EVEN GROOT / VERSCHILLEND
aangrijpingspunt: HETZELFDE / VERSCHILLEND
richting: DEZELFDE / VERSCHILLEND
zin: DEZELFDE / VERSCHILLEND
•
•
grootte: DEZELFDE / VERSCHILLEND
Beide auto's rijden even snel.
aangrijpingspunt: HETZELFDE / VERSCHILLEND
richting: DEZELFDE / VERSCHILLEND
zin: DEZELFDE / VERSCHILLEND
grootte: EVEN GROOT / VERSCHILLEND
•
•
16
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
2 Maak een eenvoudige schets en teken de snelheidsvectoren.
a Kleine Jan steekt een zebrapad over net nadat een auto voorbijgereden is.
2b Seppe en Katrien zitten op de draaimolen in een pretpark.
Seppe zit meer aan de buitenkant dan Katrien.
+3.6 Verandering van bewegingstoestand
Experiment
Probleemstelling
Wat gebeurt er met de bewegingstoestand van de hand als
de boeken onverwacht worden weggenomen?
Wat verwacht je?
□ Er gebeurt niets met de hand.
□ De hand beweegt omhoog.
□ De hand beweegt omlaag.
Materiaal
blinddoek
stapeltje boeken of ander zwaar voorwerp
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 17
Werkwijze
Blinddoek een van je klasgenootjes.
Laat hem of haar een stapeltje boeken of een zwaar voorwerp op één hand en met
gestrekte arm in evenwicht houden.
Neem op een onverwacht ogenblik plots de doos langs boven weg.
Waarneming
Wat gebeurt er met de hand van je klasgenoot? __________________________________________________
______________________________________________________________________________________________________
Kun je verklaren hoe dat komt?_____________________________________________________________________
______________________________________________________________________________________________________
Het zware voorwerp ligt stil op je hand. We zeggen dat het voorwerp in_____________________ is
ten opzichte van je hand. De snelheid van het voorwerp is op dat ogenblik ____________________
Neem je het zware voorwerp weg, dan beweegt de hand met een bepaalde snelheid verticaal
naar boven.
Besluit
Met de bewegingstoestand van een voorwerp bedoelen we de toestand van rust of
beweging van dat voorwerp.
De bewegingstoestand wordt bepaald door de snelheid van het voorwerp op dat ogenblik.
+ 3.6.1 Enkele voorbeelden
Je smartphone die op je bureau ligt, wordt aangetrokken door de aarde. Je bureau
verhindert dat hij op de grond valt en moet dus een even grote maar tegengestelde
kracht uitoefenen op je smartphone. Je smartphone is in rust. De snelheidsvector blijft
gelijk in richting, zin en grootte.
De hond in de auto beweegt met een constante
snelheid op een rechte baan. (= ERB). Zijn
bewegingstoestand verandert niet. De hond en auto
zijn dus in rust.
18
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
Op de foto zie je het ISS (International Space Station) in
een baan om de aarde. Het ISS beweegt met een
bepaalde snelheid en volgens een bepaalde richting en
zin door de ruimte. Door de motoren te ontsteken kan
het Space Center sneller of trager gaan bewegen of van
richting veranderen. De motorkracht kan dus de
bewegingstoestand van het ISS veranderen.
Je staat aan de bushalte te wachten. De bus komt aangereden, remt af en stopt. Door
de remkracht verandert de snelheid van grootte. De richting en zin van de snelheid
veranderen niet.
De gondels van een reuzenrad maken een
cirkelvormige beweging. De snelheid van de gondels
verandert voortdurend van richting en zin maar de
grootte van de snelheid verandert niet. Een beweging
op een cirkelvormige baan waarbij de grootte van de
snelheid constant blijft, maar de richting en de zin
voortdurend verandert, is een eenparig cirkelvormige beweging (ECB).
Samengevat
De bewegingstoestand en dus de snelheid van een voorwerp verandert niet als de
snelheidsvector gelijk blijft in richting, zin en grootte. (v = 0)
De bewegingstoestand van een voorwerp verandert als één of meerdere kenmerken van de
snelheidsvector veranderen. (v ≠ 0)
Alle bewegingen waarbij de snelheidsvector
niet constant is, zijn veranderlijke bewegingen.
De bewegingstoestand van een voorwerp verandert onder invloed van een kracht.
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 19
+3.6.2 Oefeningen
1 Op de tekening is de snelheidsvector van de wagen getekend op verschillende tijdstippen.
Hoe zie je dat de bewegingstoestand van de wagen verandert?
___________________________________________________________________________________________________
2 Omcirkel het juiste antwoord.
a. Je glijdt op een slee een steile helling af.
rust / ERB / ECB / veranderlijke beweging
b. Een formule-1 wagen neemt met een constante snelheid een bocht van 180° op het
circuit van Zolder.
rust / ERB / ECB / veranderlijke beweging
c. Je fietst over een rechte weg naar school, de wind op kop. Toch slaag je erin je
snelheid constant te houden.
rust / ERB / ECB / veranderlijke beweging
d. De paardenmolen op de kermis komt langzaam tot stilstand.
rust / ERB / ECB / veranderlijke beweging
e. Je motorfiets valt zonder benzine. Je bolt langzaam uit op een vlakke rechte weg.
rust / ERB / ECB / veranderlijke beweging
20
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
3 Kruis in de tabel voor elk interval uit het s(t)- en v(t)-diagram de juiste beweging aan.
s (m)
F
E
B
Rust
ERB
VB
Rust
ERB
VB
AB
BC
CD
DE
EF
C
D
A
t (s)
v (m/s)
A
AB
BC
CD
DE
B
E
C
D
t (s)
4 Welke beweging volgen de vliegtuigjes op deze kermisattractie? ______________________________
Hoe kan je dat zien op de tekening?
__________________________________________________________
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 21
5 Het balletje in de roulette draait met een constante snelheid op een
cirkelvormige baan. Beantwoord volgende vragen.
a. Is dit balletje in rust?_________
b. Voert het een eenparig rechtlijnige beweging uit? ____________
c. Is de grootte van de snelheid van het balletje constant? _______________
d. Is de richting en zin van de snelheid van het balletje constant? ____________
e. Is
f.
constant? ______________
Verandert de bewegingstoestand van het balletje? ______________
g. Werkt er een kracht op het balletje? __________
+3.7
Resulterende kracht en beweging
Eerder zagen we dat de bewegingstoestand van een voorwerp verandert als er een kracht op
uitgeoefend wordt. Als meerdere krachten op een voorwerp werken, zie je het effect van de
resulterende kracht.
Verder onderzoeken we de invloed van een kracht op de snelheidsvector.
+3.7.1 De snelheid van het voorwerp verandert niet
A Het voorwerp ligt stil
Deze leguaan is in RUST / BEWEGING
Zijn snelheid is gelijk aan ________________________
Een kwartier later ligt de leguaan nog altijd rustig te
slapen. Zijn snelheid is dus nog steeds gelijk aan
__________________ Hoe schrijf je dit in symbolen ?
_____________________________________________________
Op de leguaan werken twee krachten namelijk
- de zwaartekracht ( ) en
- de kracht van de tak op de leguaan ( ) .
Wat kan je zeggen over de grootte, de richting en de zin van beide krachten?
22
de grootte: EVEN GROOT / VERSCHILLEND
de richting: DEZELFDE / VERSCHILLEND
de zin: DEZELFDE / VERSCHILLEND
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
Hoe groot is de resulterende kracht (
)? ________________________________________________________
Geef dit met een zwarte kleur weer op de tekening.
Teken de snelheid naast de foto met groen.
B Het voorwerp beweegt met een constante snelheid in dezelfde richting en zin
De fietser rijdt met een constante snelheid over een rechte baan.
Als je fietst, veroorzaak je een voorwaarts gerichte aandrijfkracht (
).
Door de wrijving tussen de banden en de baan, de wrijving met de lucht en de wrijving tussen
de bewegende onderdelen van de fiets ontstaat een achterwaarts gerichte wrijvingskracht
(
). De wrijvingskracht werkt de aandrijfkracht tegen.
Wat kan je zeggen over de grootte, de richting en de zin van beide krachten?
de grootte: EVEN GROOT / VERSCHILLEND
de richting: DEZELFDE / VERSCHILLEND
de zin: DEZELFDE / TEGENGESTELD
Hoe groot is de resulterende kracht (
)? ________________________________________________________
Geef dit met een blauwe kleur weer op de tekening.
Hoe groot is de snelheidsverandering ?____________________________________________________________
Teken de snelheid
en de snelheid
met groen op de figuur.
Samengevat
Een voorwerp ondergaat geen snelheidsverandering wanneer het:
in rust blijft,
met een constante snelheid in dezelfde richting en zin blijft bewegen.
De resulterende kracht op het voorwerp is dan nul.
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 23
Als
v = 0 dan is Fres = 0
+3.7.2 Verandering van snelheid bij een rechtlijnige beweging
A De grootte van de snelheid neemt toe
Duw je wat harder op de trappers van je fiets, dan wordt de aandrijfkracht ____________________
dan de wrijvingskracht.
De resulterende kracht op je fiets is nu niet meer gelijk aan ________________________
De resulterende kracht is ____________________________________ gericht.
Wat is het gevolg hiervan? ________________________________________________________________________
Teken de snelheid
en de snelheid
met groen op de figuur.
B De grootte van de snelheid neemt af
Duw je minder hard op de trappers of rem je dan wordt de aandrijfkracht ______________________
dan de wrijvingskracht.
De resulterende kracht is dan niet meer gelijk aan ________________________
De resulterende kracht is ______________________________________gericht.
Wat is het gevolg hiervan?__________________________________________________________________________
24
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
Teken de snelheid
en de snelheid
met groen op de figuur.
Samengevat
De snelheidsvector van een voorwerp verandert, als de resulterende kracht op dat voorwerp
niet gelijk is aan 0.
Als v ≠ 0 dan is Fres ≠ 0
Hoe groter de resulterende kracht op een voorwerp, hoe groter zijn snelheidsverandering.
+3.7.3 Verandering van snelheid bij een cirkelvormige beweging
Steek een dun touwtje van ongeveer 50 cm door een
dun buisje. Bevestig aan beide uiteinden een massa m1
en een massa m2 met m2 > m1.
Maak een draaiende beweging met het buisje zodanig dat m1
op een constante afstand van het buisje blijft ronddraaien.
De grootte van de snelheid van m1 wordt GROTER / KLEINER /
BLIJFT GELIJK.
Massa m1 beschrijft dus een eenparig cirkelvormige beweging
(ECB).
Teken in de figuur hiernaast de snelheidsvector voor een beweging
A
in wijzerzin in punt A en in punt B als je weet dat haar grootte
niet verandert.
Beschrijf de richting en de zin van de snelheidsvector.
B
richting:______________________________________________________________________________________________
zin:___________________________________________________________________________________________________
De kracht die de eenparig cirkelvormige beweging doet ontstaan, wordt de
middelpuntzoekende of centripetale kracht (
) genoemd. Ze is altijd naar het middelpunt
van de cirkel gericht. Teken ze in A en B.
Wat is de richting en de zin van middelpuntzoekende kracht?
richting:______________________________________________________________________________________________
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 25
zin:___________________________________________________________________________________________________
Stel dat het touwtje plots breekt. Welke beweging zou de massa m1 dan maken?
______________________________________________________________________________________________________
______________________________________________________________________________________________________
Hoe wordt de middelpuntzoekende kracht opgewekt in volgende voorbeelden?
• Bij het hamerslingeren beweegt de kogel rond aan een touw.
_____________________________________________________________________________________________________
• We ‘centrifugeren’ onze natte was in een wasmachine.
____________________________________________________________________________________________________
• De maan beweegt in een nagenoeg cirkelvormige baan omheen de aarde.
_____________________________________________________________________________________________________
Samengevat
Wanneer een voorwerp een cirkelvormige beweging beschrijft, dan verandert zijn snelheid
voortdurend van richting.
De kracht die de eenparig cirkelvormige beweging doet ontstaan, wordt de
middelpuntzoekende (
) genoemd.
De zin van de middelpuntzoekende kracht is altijd naar het middelpunt van de cirkel gericht.
De richting staat loodrecht op de richting van de snelheidsvector .
26
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
+3.7.4
Oefeningen
1 Bij een voorwerp dat valt over enkele kilometers blijft de zwaartekracht nagenoeg constant.
De wrijvingskracht die de lucht verticaal omhoog uitoefent, neemt echter toe met de snelheid.
In figuur a, bij het begin van de sprong, is de snelheid nog klein en de wrijvingskracht van de
lucht eveneens. De snelheid zal verder vergroten.
Teken de resulterende kracht (
) met zwart bij iedere situatie op de tekening en benoem de
vector.
In figuur b is de snelheid TOEGENOMEN / AFGENOMEN. De wrijvingskracht is ook
TOEGENOMEN / AFGENOMEN.
In figuur c is de valsnelheid constant geworden. De wrijvingskracht is dan GROTER / KLEINER /
EVEN GROOT dan de zwaartekracht.
In figuur d wordt het valscherm geopend en neemt de snelheid plots TOE / AF
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 27
De wrijvingskracht neemt dan plots TOE / AF. De zin van de resultante is naar BENEDEN /
BOVEN gericht en heeft dus een TEGENGESTELDE / DEZELFDE zin dan de beweging.
In figuur e daalt het valscherm verder en blijft de snelheid opnieuw _____________________________
2 In onderstaande figuren verandert de bewegingstoestand van het systeem niet.
Teken de krachten die op het systeem werken. Hoe groot is de resulterende kracht op ieder
systeem?__________________________________________________________________________________________
Touw
Bloempot op tafel
3 In onderstaande figuren verandert de bewegingstoestand van het systeem.
Teken de resulterende kracht op het systeem. Schrijf onder iedere figuur welk effect de
resulterende kracht op het systeem heeft.
vrije val
lancering raket
tractor remt af
zijdelingse windstoot
4 Een fietser rijdt op een rechte baan met een constante snelheid. Hoe groot is de
resulterende kracht op de fietser? ______________________________________________________________
Toch moet de fietser een kracht uitoefenen op de pedalen. Leg uit waarom.
28
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
___________________________________________________________________________________________________
5 Thalia draait rondjes op een draaimolen in de speeltuin. Is er een verandering van de
snelheidsvector? Leg uit.
________________________________________________________________________________________________
________________________________________________________________________________________________
Plots wordt Thalia gestoken door een wesp. Ze schrikt en laat zich los.
Volgens welke richting zal Thalia van de draaimolen
geslingerd worden?
1 - 2 - 3 - 4
6 Siebe schiet met een geweer een balletje verticaal omhoog.
Welke krachten werken op het balletje tijdens de
verplaatsing naar boven? De weerstandskracht van de lucht op het
balletje wordt verwaarloosd.
A
B
heengaande beweging
C
D
teruggaande beweging
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 29
a. Teken in het zwaartepunt, aangegeven op de as in 4 verschillende posities, de inwerkende
kracht(en) op figuur A en C, bij elke stand van het balletje.
b. Teken op figuur B en D de snelheidsvectoren in de verschillende zwaartepunten. In de
hoogste positie is v = _______________________
c. Vergelijk de richting en de zin van de kracht met die van de snelheid voor de heengaande
beweging.
richting_______________________________________________________________________________________
zin____________________________________________________________________________________________
Welk effect heeft deze kracht op de snelheid?
___________________________________________________________________________________________________
d. Vergelijk de richting en de zin van de kracht met die van de snelheid voor de teruggaande
beweging.
richting_______________________________________________________________________________________
zin____________________________________________________________________________________________
Welk effect heeft deze kracht op de snelheid?
___________________________________________________________________________________________________
e. Vergelijk de snelheid van het balletje in iedere positie bij de heengaande en teruggaande
beweging. Wat kan je hieruit besluiten?
___________________________________________________________________________________________________
___________________________________________________________________________________________________
7 Het nemen van een bocht (een cirkelvormige beweging) tegen een constante snelheid is een
verandering van bewegingstoestand. Leg uit waarom.
____________________________________________________________________________________________________
Beschrijf de kracht die verantwoordelijk is voor deze cirkelvormige beweging.
____________________________________________________________________________________________________
____________________________________________________________________________________________________
Ondergaat Lambik op de tweede figuur een verandering van bewegingstoestand? __________
30
KRACHT . ARBEID . VERMOGEN . ENERGIE
Bijlage p. 169e
Leg uit wat hier gebeurt.
__________________________________________________________________________________________________
__________________________________________________________________________________________________
Bijlage p. 169e
KRACHT . ARBEID . VERMOGEN . ENERGIE 31