Oefening 11 (p29)

1ste Kandidatuur ARTS of TANDARTS
Academiejaar 2002-2003
BIOFYSICA: WERKZITTING 08 en 09 (Oplossingen)
ELEKTRISCHE KRINGEN
Oefening 11 (p29)
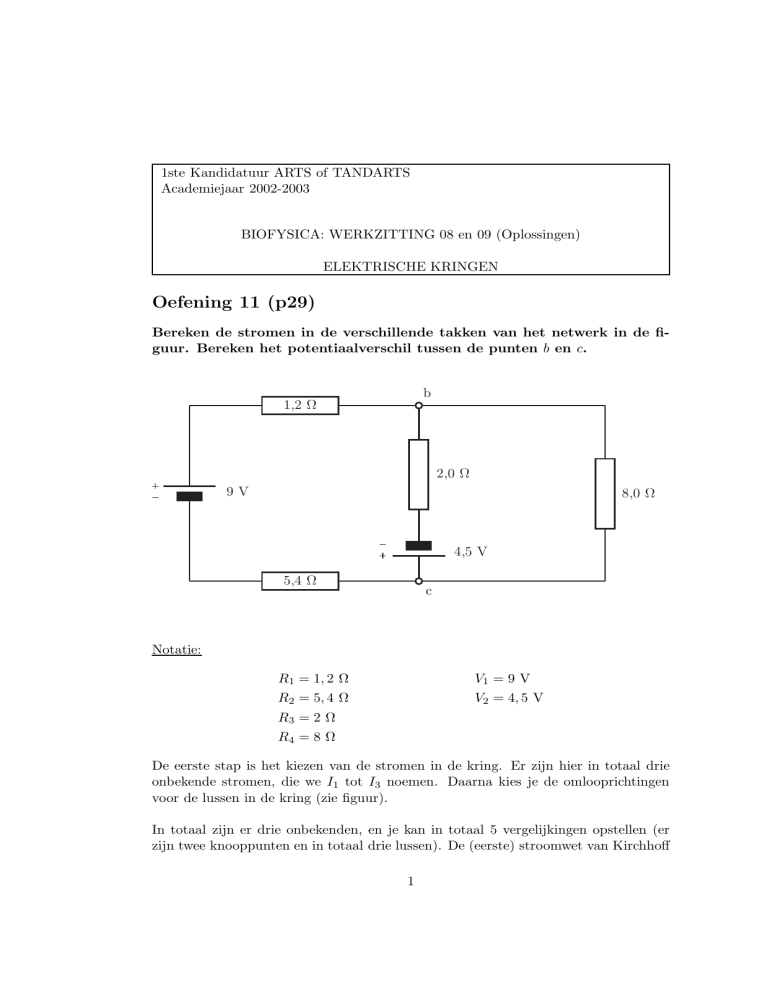
Bereken de stromen in de verschillende takken van het netwerk in de figuur. Bereken het potentiaalverschil tussen de punten b en c.
b
1,2 Ω
2,0 Ω
9V
8,0 Ω
4,5 V
5,4 Ω
c
Notatie:
R1 = 1, 2 Ω
V1 = 9 V
R2 = 5, 4 Ω
V2 = 4, 5 V
R3 = 2 Ω
R4 = 8 Ω
De eerste stap is het kiezen van de stromen in de kring. Er zijn hier in totaal drie
onbekende stromen, die we I1 tot I3 noemen. Daarna kies je de omlooprichtingen
voor de lussen in de kring (zie figuur).
In totaal zijn er drie onbekenden, en je kan in totaal 5 vergelijkingen opstellen (er
zijn twee knooppunten en in totaal drie lussen). De (eerste) stroomwet van Kirchhoff
1
I1
I2
b
1,2 Ω
I3
2,0 Ω
9V
1
2
8,0 Ω
4,5 V
5,4 Ω
c
uitschrijven in de knooppunten b en c levert de volgende twee vergelijkingen:
(knooppunt b)
I1 − I3 − I2 = 0
I3 + I2 − I1 = 0
(knooppunt c)
Aangezien je de tweede vergelijking uit de eerste kan bekomen door alle tekens te
veranderen, zijn deze vergelijkingen niet onafhankelijk. Je kan er slechts één gebruiken
om de oplossing te bekomen. Aangezien je drie onbekenden hebt (en je dus drie
vergelijkingen nodig hebt) moet je nog twee andere vergelijkingen neerschrijven. Deze
vind je met de (tweede) spanningswet van Kirchhoff:

(lus 1)

 V1 − R1 I1 − R3 I3 + V2 − R2 I1 = 0
=0
(lus 2)
− V2 + R3 I3 − R4 I2


=0
(de buitenste kring)
V1 − R1 I1 − R4 I2 − R2 I1
Ook deze drie vergelijkingen zijn niet onafhankelijk. Door de eerste twee op te tellen
bekom je de derde vergelijking. We zullen hier de eerste twee vergelijkingen nemen,
en deze combineren met de vergelijking die we overhielden bij de stroomwet van
Kirchhoff. Het stelsel dat moet opgelost worden om de onbekende stromen I1 , I2 en
I3 te bepalen is dus:

=0
(1)

 I1 − I3 − I2
(2)
V1 − (R1 + R2 )I1 − R3 I3 + V2 = 0


=0
(3)
− V2 + R3 I3 − R4 I2
Uit vergelijking (1) vind je dat I1 = I2 + I3 . Vul dit resultaat in vergelijking (2) in:

= I1

 I3 + I2
V1 + V2 − (R1 + R2 )(I2 + I3 ) − R3 I3 = 0


=0
− V2 + R3 I3 − R4 I2
2
Je kan nu de twee laatste vergelijkingen herschrijven naar I2 :

I1 = I3 + I2





V1 + V2 − (R1 + R2 + R3 )I3
I2 =
R1 + R2




 I2 = −V2 + R3 I3
R4
Door nu de twee laatste vergelijkingen aan elkaar gelijk te stellen krijg je een gesloten
vergelijking voor I3 . Deze kan je dan oplossen:
−V2 + R3 I3
V1 + V2 − (R1 + R2 + R3 )I3
=
R1 + R2
R4
⇔
I3 ≈ 1, 679 A
Met dit gegeven kan je nu I1 en I2 berekenen:
I1 ≈ 1, 536 A
I2 ≈ −0, 142 A
I3 ≈ 1, 679 A
Het spanningsverschil tussen punten b en c kan je berekenen uit de stroom die door
de weerstand R4 gaat. De weerstand R4 staat immers parallel over de punten b en c,
dus de spanning tussen beide punten is gegeven door:
Vbc = −I2 R4 ≈ 1, 14 V
Oefening 12 (p30)
Het netwerk in de figuur is in de stationaire toestand. Zoek de stroom
door de weerstand en bereken het potentiaalverschil over de condensator.
Bereken ook de lading op de condensator.
Als de kring in de stationaire toestand is, wil dit zeggen dat de condensator volledig
opgeladen is: er vloeit geen stroom meer naar de condensator. In deze toestand
speelt de condensator de rol van een onderbreking in de kring in die tak. Je kan met
andere woorden de condensatortak gewoon weglaten uit de beschrijving.
In dat geval krijg je een serieschakeling van drie weerstanden. De totale weerstand
van de kring kan je berekenen met de optelregel voor serieweerstanden:
Ri
Rtot =
i
Je vindt door alles op te tellen dat Rtot = 12 Ω. De stroom door deze serieschakeling
kan je met de wet van Ohm berekenen voor de totale weerstand:
I=
U
R
⇔
I=
10
5
= A
16
8
Het potentiaalverschil over de condensator is gelijk aan de spanning over de rechtse
weerstand van 4 Ω, aangezien deze parallel met de condensator geschakeld is (voor
3
b
4Ω
20 pF
10 V
8Ω
4,0 Ω
c
parallel geschakelde componenten weet je dat de spanning over elk van deze componenten gelijk is). De spanning over deze weerstand kan je opnieuw berekenen met de
wet van Ohm, deze keer toegepast op de weerstand van 4 Ω:
⇔
U = IR
UC =
5
V
2
Nudat de spanning over de condensator gekend is, kan je de lading eenvoudig berekenen uit de capaciteit, met de formule U = Cq :
q = UC
q = 50 pC = 50 · 10−12 C
⇔
4
Oefening 20 (p31)
In het netwerk in de figuur is R1 = 200 kΩ, R2 = 100 kΩ, C = 15 nF en
U = 100 mV. Bereken de stroom door de takken (1,4) en (1,2,3,4) vanaf
het moment dat de schakelaar gesloten wordt. Bereken ook het potentiaalverschil tussen 1 en 4 als functie van de tijd.
2
i2
1
i
C
R2
R1
i1
3
U
4
De eerste stap is weer het kiezen van de knooppunten (in dit geval zijn dit de punten
1 en 4 op de figuur) en het kiezen van de lussen en hun omloopszin. Het uitschrijven
van de eerste wet van Kirchhoff levert voor elk van de knooppunten:
(knooppunt 1)
i(t) − i1 (t) − i2 (t) = 0
i1 (t) + i2 (t) − i(t) = 0
(knooppunt 4)
Hier is weer de tweede vergelijking op het minteken na gelijk aan de eerste. Je kan
de tweede vergelijking dus niet gebruiken om de onbekende stromen te bepalen.
Vooraleer je de tweede wet van Kirchhoff kan toepassen, moet je eerst nagaan welke
plaat van de condensator positief opgeladen wordt. De plaat van de condensator die
verbonden is met de positieve pool van de batterij laadt positief op, de andere plaat
laadt negatief op. Als je de condensator van de + naar de - kant doorloopt moet je
deze positief meetellen, in het andere geval negatief. Hiermee kan je de tweede wet
van Kirchhoff uitschrijven:

=0
(lus 1)

 UC (t) − i2 (t)R2
=0
(lus 2)
U − i(t)R1 − UC (t)


(de buitenste kring)
U − i(t)R1 − i2 (t)R2 = 0
Ook hier is er een vergelijking die je niet kan gebruiken: de som van de eerste twee
vergelijkingen geeft terug de derde. We zullen hier enkel de eerste twee gebruiken.
5
2
i2
i
1
C
R2
1
R1
2
i1
3
U
4
In totaal hebben we dan de vergelijkingen:

=0

 i(t) − i1 (t) − i2 (t)
=0
UC (t) − i2 (t)R2


U − i(t)R1 − UC (t) = 0
(1)
(2)
(3)
Noteer de lading op de condensator als q(t). Noteer de spanning over de condensator
UC (t) = q(t)
C , dan geeft vergelijking (2):
i2 (t) =
q(t)
R2 C
Vergelijking (3) kan je herschrijven door i(t) = i1 (t) + i2 (t) te substitueren en UC (t)
in te vullen:
q(t)
=0
U − i1 (t) + i2 (t) R1 −
C
Vul nu de daarnet bekomen uitdrukking voor i2 (t) in:
q(t)
q(t)
R1 −
=0
U − i1 (t) +
R2 C
C
De verandering van de lading op de condensator dq(t)
dt is gegeven door de stroom
i1 (t), aangezien dit net de stroom is die naar de condensator vloeit. Deze substitutie
doorvoeren geeft:
q(t)
q(t)
dq(t)
+
R1 −
=0
U−
dt
R2 C
C
Het herschrijven van deze differentiaalvergelijking levert:
R1 + R2
U
dq(t)
+ q(t)
=
dt
R1 R2 C
R1
6
Dit is een eerste orde lineaire differentiaalvergelijking van de vorm dX
dt −αX(t) = αXd .
In het formularium vind je de oplossing van deze vergelijking als X(t) = C0 e−αt +Xd .
Toegepast op deze differentiaalvergelijking krijg je als oplossing:
q(t) = C0 e−αt +
1 U
α R1
α=
R1 + R2
R1 R2 C
De constante C0 kan je bepalen uit de beginvoorwaarde: op tijdsstip t = 0 is de lading
op de condensator gelijk aan nul (we nemen aan dat de condensator niet opgeladen
is als we de spanningsbron aanschakelen):
q(t = 0) = 0
⇔
C0 = −
1 U
α R1
De volledige oplossing is dan:
q(t) =
1 U 1 − e−αt
α R1
α=
R1 + R2
R1 R2 C
Het is nu een koud kunstje om de uitdrukking voor de stromen i1 (t) en i2 (t) te
bekomen:

dq(t)
U −αt


⇔
i1 (t) =
e
 i1 (t) =
dt
R1

q(t)
1 U 
 i2 (t) =
⇔
i2 (t) =
1 − e−αt
R2 C
α R1
Door de waarde van α in te vullen vind je als eindresultaat:

U − RR1 R+RC2 t


(t)
=
e 1 2
i
1

R1
R +R
R2 U

− R1 R C2 t

 i2 (t) =
1−e 1 2
R1 + R2
7
Oefening 24 (p32)
In een kring zijn een condensator met capaciteit
stand van 1,5 kΩ in serie geschakeld met een bron
300 sin(2πf t), f = 50 Hz. Hoe verloopt de stroom als
Bereken ook het gemiddeld vermogen geleverd door
9 µF, en een weermet spanning v(t) =
functie van de tijd ?
de bron.
Noteer de spanning als v(t) = V sin(ωt). Als de spanning harmonisch varieert, dan
kan je verwachten dat de stroom door de kring met dezelfde frequentie harmonisch
varieert, maar eventueel een fasefactor φ voor- of achterloopt:
v(t) = V sin(ωt)
i(t) = I sin(ωt + φ)
Om de stroom i(t) volledig te bepalen moet je de amplitude I en de fasefactor φ
berekenen.
Aangezien je hier met een serieschakeling van een wisselspanningsbron, weerstand en
condensator te maken heb, kan je meteen de tweede wet van Kirchhoff neerschrijven:
v(t) = vR (t) + vC (t)
Voor een serieschakeling onder wisselspanning moet je weten dat de spanning over de
weerstand in fase loopt met de wisselstroom, en dat de spanning over de condensator
90◦ in fase achterloopt:

i(t) = I sin(ωt + φ)




(in fase)
vR (t) = VR sin(ωt + φ)

π


 vC (t) = VC sin ωt + φ −
(90◦ achter in fase)
2
De tweede wet van Kirchhoff geeft dan de volgende gelijkheid tussen de verschillende
spanningen:
π
V sin(ωt) = VR sin(ωt + φ) + VC sin ωt + φ −
2
Je kan deze gelijkheid ofwel onmiddelijk oplossen, ofwel oplossen met de methode
van fasoren.
Om de methode van fasoren te gebruiken, kan je best de volgende werkwijze toepassen:
1. Teken in het fasorenvlak een stroomvector i(t). De grootte van deze vector is
net de amplitude I van de wisselstroom. Deze vector maakt een hoek ωt+φ met
de x-as (dit is net het argument van de sinus die de wisselstroom i(t) beschrijft).
2. Teken de fasor vR (t). Dit is een vector met grootte VR , de amplitude van
de wisselspanning over de weerstand, die volgens de stroomvector i(t) ligt. Dit
laatste is zo omdat de spanning over de weerstand in fase is met de wisselstroom.
8
3. Teken de fasor vC (t). Deze vector heeft als grootte VC , en loopt 90◦ achter op
de stroomvector.
4. De totale spanningsfasor v(t) kan je bekomen door de vectorsom vC (t) + vR (t)
te maken1 . Deze vectorsom kan je het eenvoudigst uitwerken met de parallellogram constructie
Deze stappen zijn samengevat in de volgende figuur:
y
ωt
i(t)
vR(t)
x
φ
v(t)
vC (t)
Uit de figuur kan je allerlei verbanden afleiden tussen alle grootheden en op die manier
de amplitude I bepalen:
 2
2
2
(stelling van Pythagoras)
 V = VR + VC
V
 tan(φ) = C
(definitie tangens)
VR
Nu kan je de formules voor de reactantie gebruiken om de amplitudes VC en VR te
bepalen:

 VR = IR
V = IX
⇔
 VC = I
ωC
1
In werkelijkheid zijn dit geen vectoriele grootheden! Je gebruikt hier het truukje met de fasoren
om de berekening te vereenvoudigen, en daar voeg je de fictieve vectorinterpretatie toe.
9
Dit invullen geeft:


2
2

 V = I R2 +


 tan(φ) =
1
(ωC)2
1
ωRC
Oplossen naar de twee onbekenden I en φ levert als resultaat:


I=



V
≈ 0, 195 A
1
R2 + (ωC)
2


1

 φ = Bgtan
≈ 13, 5◦
ωRC
Het (gemiddeld) vermogen in een wisselspanningskring is steeds gegeven door:
Pg = Vg Ig cos(φ)
Gebruik makend van het feit dat voor een harmonisch varierende wisselstroom en
wisselspanning de gemiddelde spanning en stroom gegeven zijn door Ig = √I2 en
Vg =
V
√
2
respectievelijk:
VI
cos(φ)
2
De fasefactor φ is net het faseverschil tussen de stroom i(t) en spanning v(t) dat we
net berekend hebben. Invullen en uitwerken levert:
Pg =
Pg ≈ 28, 4 W
10
Oefening 26 (p32)
Judy wil de FM-ontvanger afstemmen op een frequentie van 99,7 MHz.
Hiervoor wordt een RLC-seriekring gebruikt met R = 12 Ω en L = 14 µH.
Wat is de capaciteit van de condensator ?
Het afstemmen van een FM-ontvanger komt neer op het in resonantie brengen van de
RLC-kring, waarbij de resonantiefrequentie net de gewenste radiofrequentie is. Bij
resonantie zal immers de stroom door de kring het grootst zijn:
I=
V
R2 + ωL −
1
ωC
ωR = √
2
1
LC
Bij ω = ωR krijg je als uitdrukking voor de stroom:
I=
V
R
en dit is de grootst mogelijke waarde (voor eender welke andere ω zal de ω-term onder
de vierkantswortel niet meer wegvallen, en aangezien deze wegens het kwadraat altijd
positief is, deel je dus voor eender welke andere ω door iets dat groter is dan R. Het
eindresultaat zal dan altijd kleiner zijn). Bij een radio-ontvanger is een grote stroom
door de kring bijvoorbeeld handig om de luidsprekers aan te sturen.
De gewenste frequentie f is in dit geval f = 99, 7·106 Hz. De hiermee overeenkomende
(resonantie) hoekfrequentie ωR = 2πf rad/s. De capaciteit die hiervoor nodig is kan
je dan berekenen uit de formule voor de resonantiefrequentie van een RLC-kring:
ωR = √
1
LC
1
LC
1
⇔ C= 2 2
4π f L
⇔ 2πf = √
⇔ C ≈ 1, 82pF
11
Appendix: Analyseschema voor elektrische kringen
1. Nummer de knooppunten in de kring.
2. Kies in elke tak van de kring een stroomzin.
3. Kies in elke lus een omloopzin.
4. Schrijf de twee wetten van Kirchhoff uit: voor elk knooppunt schrijf je de eerste
wet van Kirchhoff uit:
Ii = 0
i
Hierbij reken de stromen die toekomen in een knooppunt positief, en de stromen
die vertrekken in een knooppunt negatief. Daarna schrijf je de tweede wet van
Kirchhoff uit voor elke lus:
Vi = 0
i
Hierbij reken je:
• De spanning over een weerstand negatief als de omloopzin gelijk is aan
de stroomzin in die tak (de spanning over een weerstand daalt volgens de
stroomrichting).
• De spanning van een batterij telt positief mee als je van de - naar de +
pool gaat (de spanning over een batterij verhoogt van - naar +).
• Een condensator reken je op dezelfde manier als een batterij mee. De
plaat van de condensator die met de + pool van de batterij verbonden
is zal positief opgeladen worden, de kant die met de - pool verbonden is
negatief.
5. Los het stelsel dat je zo bekomt op naar de onbekenden (de stromen in de
kring).
Tim Jacobs - 24 december 2002
12