Vergelijkingen oplossen

Vergelijkingen oplossen
Eerstegraads vergelijkingen
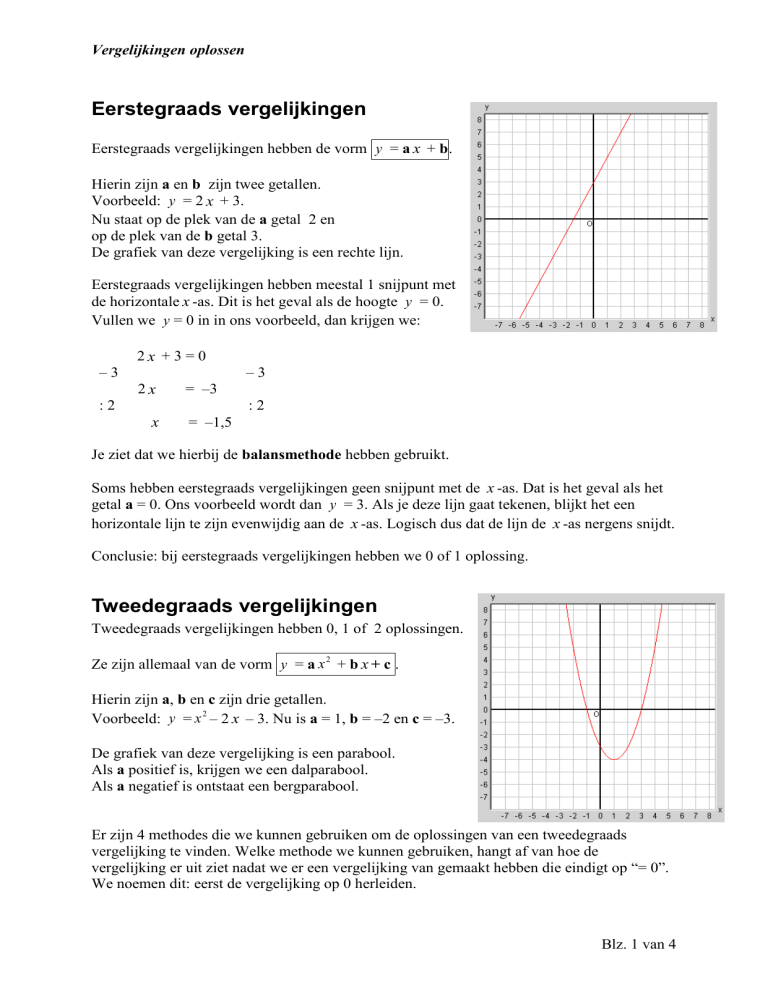
Eerstegraads vergelijkingen hebben de vorm y = a x + b.
Hierin zijn a en b zijn twee getallen.
Voorbeeld: y = 2 x + 3.
Nu staat op de plek van de a getal 2 en
op de plek van de b getal 3.
De grafiek van deze vergelijking is een rechte lijn.
Eerstegraads vergelijkingen hebben meestal 1 snijpunt met
de horizontale x -as. Dit is het geval als de hoogte y = 0.
Vullen we y = 0 in in ons voorbeeld, dan krijgen we:
2x +3=0
–3
–3
2x
= –3
:2
:2
x
= –1,5
Je ziet dat we hierbij de balansmethode hebben gebruikt.
Soms hebben eerstegraads vergelijkingen geen snijpunt met de x -as. Dat is het geval als het
getal a = 0. Ons voorbeeld wordt dan y = 3. Als je deze lijn gaat tekenen, blijkt het een
horizontale lijn te zijn evenwijdig aan de x -as. Logisch dus dat de lijn de x -as nergens snijdt.
Conclusie: bij eerstegraads vergelijkingen hebben we 0 of 1 oplossing.
Tweedegraads vergelijkingen
Tweedegraads vergelijkingen hebben 0, 1 of 2 oplossingen.
Ze zijn allemaal van de vorm y = a x 2 + b x + c .
Hierin zijn a, b en c zijn drie getallen.
Voorbeeld: y = x 2 – 2 x – 3. Nu is a = 1, b = –2 en c = –3.
De grafiek van deze vergelijking is een parabool.
Als a positief is, krijgen we een dalparabool.
Als a negatief is ontstaat een bergparabool.
Er zijn 4 methodes die we kunnen gebruiken om de oplossingen van een tweedegraads
vergelijking te vinden. Welke methode we kunnen gebruiken, hangt af van hoe de
vergelijking er uit ziet nadat we er een vergelijking van gemaakt hebben die eindigt op “= 0”.
We noemen dit: eerst de vergelijking op 0 herleiden.
Blz. 1 van 4
Vergelijkingen oplossen
De vergelijking op nul herleiden
Stel je hebt de vergelijking x 2 + 4 = 2 x + 7.
Deze vergelijking bestaat uit 2 termen links van het “=”-teken en 2 termen
rechts van het “=”-teken. Bij het op nul herleiden gaan we eerst alle termen naar links halen.
Daarbij gebruiken we weer de balansmethode.
x2 + 4 = 2 x + 7
–2 x
–2 x
x – 2x+ 4 = 7
2
–7
–7
x – 2x+ 4 – 7 = 0
x2 – 2 x – 3 = 0
2
Methode 1: worteltrekken
De vergelijking bevat geen term met x .
Voorbeeld: x 2 – 9 = 0.
In zo’n geval kunnen we de balansmethode toepassen en gaan worteltrekken.
x2 – 9 = 0
+9
+9
x
2
=9
x = 3 of x = –3
Let op: bij worteltrekken zijn er altijd twee uitkomsten mogelijk. Ga maar na.
We zoeken een getal wat met zichzelf vermenigvuldigd 9 oplevert.
Dat geldt natuurlijk voor 3, want 3  3 = 9.
Maar er geldt ook (–3)  (–3) = 9. Dus–3 is ook een oplossing.
Methode 2: ontbinden in factoren
De vergelijking bevat een term met x 2 en term met een x en geen getal c voor het “=”-teken.
Voorbeeld: 4 x 2 + 12 x = 0.
In zo’n geval gaan we de gemeenschappelijke factor buiten haakjes halen.
In dit geval kunnen we beide termen delen door factor 4 x . Die zetten we voor de haakjes.
Tussen de haakjes blijft staan wat er overblijft van beide termen:
4 x 2 + 12 x = 0
4 x  ( x + 3) = 0
Tip: controleer jezelf door de haakjes weer weg te werken. 4 x x = 4 x 2 en 4 x  3 = 12 x .
Nu gaan we de factoren in 2 hokjes plaatsen en geven die hokjes de letters A en B:
A 
B
=0
4 x  ( x + 3) = 0
Wat blijkt nu? Dit is alleen waar als wat in hokje A staat 0 is OF als wat in hokje B staat 0 is.
Dit levert: 4 x = 0 of ( x + 3) = 0
dus:
x = 0 of x = –3.
Blz. 2 van 4
Vergelijkingen oplossen
Methode 3: de som-product methode
Als de vergelijking 3 termen bevat links van het “=“-teken, hebben we een vergelijking van
de vorm a x 2 + b x + c = 0.
Als a gelijk is aan 1, kunnen we de som methode toepassen. Anders is het handiger om de
abc-formule toe te passen (zie methode 4).
Voorbeeld: x 2 – 7 x + 10 = 0. Voor de x 2 staat geen getal, dus kunnen we de som-product
methode toepassen. Die werkt als volgt.
We zoeken twee getallen, waarvan de som = – 7 en het product = 10.
Nu is het een kwestie van uitproberen. Daarvoor maak je een tabel die er zo uit ziet:
Eerste getal
–3
–2
Tweede getal
–4
–5
Som
–7
–7
Product
12
10
OK?
Nee
Ja
Nu kunnen twee factoren maken, waarin we de gevonden getallen verwerken:
( x – 2)  ( x – 5) = 0.
Tip. Controleer dit weer door de haakjes weg te werken (papagaaiebek):
x  x + x  (–5) + (–2)  x + (–2)  (–5) = x 2 – 7 x + 10.
Nu we de twee factoren gevonden hebben, kunnen we ze weer in twee doosjes A en B doen.
A 
B
=0
( x – 2)  ( x – 5) = 0
Dit is alleen waar als wat in hokje A staat 0 is OF als wat in hokje B staat 0 is.
Dus ( x – 2) = 0 of ( x – 5) = 0
of x = 5.
x =2
Blz. 3 van 4
Vergelijkingen oplossen
Methode 4: de abc-formule
Als de vergelijking de vorm heeft van a x 2 + b x + c = 0 waarbij er wel een getal voor de x 2
staat, kun je het beste de abc-formule toepassen.
Voorbeeld:
2 x 2 + 5 x – 3 = 0.
Hierin is a = 2, b = 5 en c = –3.
Om te kijken of er 0, 1 of 2 oplossingen zijn, beginnen we met de Discriminant uit te rekenen.
De Discriminant D berekenen we met de formule D = b2 – 4ac .
In ons voorbeeld: D = 52 – 4  2  (–3) = 25 + 24 = 49.
Als D > 0 dan heeft de vergelijking 2 verschillende oplossingen.
Als D = 0 dan heeft de vergelijking 1 oplossing.
Als D < 0 dan heeft de vergelijking geen oplossingen en kunnen we stoppen.
In ons voorbeeld is D = 49, dus groter dan 0. We weten nu dat er 2 verschillende oplossingen
zijn. De oplossingen zelf kunnen we berekenen met abc-formule. Die ziet er als volgt uit:
x
b  D
b  D
of x 
.
2a
2a
5  49
5  49
of x 
22
22
5  7
5  7
Dus: x 
of x 
, dus x = –3 of x = 0,5.
4
4
Daar gaan we: x 
Samenvatting
Eerstegraads vergelijkingen los je altijd op met de balansmethode.
Bij tweedegraads vergelijkingen heb je keuze uit 4 verschillende methodes. Welke methode je
het beste kunt gebruiken, hangt af van hoe de vergelijking a x 2 + b x + c = 0 er uit ziet:
1. Als b = 0 (geen term met x ), gebruik je de balansmethode en worteltrekken.
2. Als c = 0 (geen getal voor het “=”-teken), ga je de gemeenschappelijke factor buiten
haakjes halen en gebruik je A  B = 0 als A = 0 of B = 0.
3. Als a = 1 (geen getal voor de x 2 ) ga je ontbinden in factoren met behulp van de
som-product methode. Daarna gebruik je A  B = 0 als A = 0 of B = 0.
4. In alle andere gevallen gebruik je de abc-formule. Hierbij bereken je eerst de
discriminant om te bepalen hoeveel oplossingen de vergelijking heeft.
Blz. 4 van 4