Jonge kinderen leren rekenen

Jonge kinderen leren rekenen
Domein: hele getallen
TAL-project
• Tussendoelen
• Tussendoelen
• Annex
• Afbeeldingen
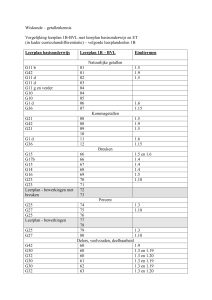
• Leerlijnen
• Leerlijnen
Het doel van het TAL-project is het beschrijven
van de tussendoelen voor het rekenonderwijs op
de basisschool. Het project geeft zicht op het
te volgen onderwijsleertraject.
Opbouw presentatie
• Voorschoolse periode: ontluikende gecijferdheid
• Groep 1 en 2 : groeiend getalbegrip
• Groep 3: rekenen tot 20
• Groep 4: rekenen tot 100
Leerlijnen en tussendoelen
Leerlijnen geven aan waar we naar toe werken.
De tussendoelen zijn markeringspunten, waarop we ons gemakkelijk
kunnen oriënteren.
Leerlijnen zijn belangrijk omdat:
• Ze overzicht en houvast geven bij de realisatie van het rekenonderwijs
• Ze belangrijke bakens uitzetten.
• Ze verschillen tussen individuele kinderen zichtbaar maken.
• Ze een inspiratiebron bij didactisch handelen kunnen vormen
• Ze ons de mogelijkheid geven ons onderwijs te verbeteren.
Ontluikende gecijferdheid
Ontluikende gecijferdheid is het proces, waarbij de kinderen op eigen
kracht geleidelijk meer besef krijgen van de verschillende betekenissen en
gebruikswijzen van de getallen en de samenhang daartussen.
De ‘3’ van ‘nummer 3 in de rij staan’ heeft iets te maken met ‘3 dropjes
krijgen’ of ‘3 jaar worden’.
Bij ontluikende gecijferdheid zijn de volgende elementen m.b.t. het begrip
van getallen te onderscheiden:
-
Het onderkennen van ‘tweeheid’, ‘drieheid’ en ‘veelheid’ als eigenschap
van een verzameling objecten.
-
Telrij kunnen opzeggen
-
Naspelen van resultatief tellen
-
Symboliseren op de vingers
Ontluikende gecijferdheid
Omstreeks het tweede levensjaar herkennen kinderen al twee of 3
voorwerpen binnen een verzameling. 2 televisies; drie boeken.
Het resultatief tellen om de hoeveelheid te bepalen zegt het kind op dat
moment nog niets.
Vaak lijkt het tellen verband te houden met het zien van een ruimtelijke
structuur.
Het opzeggen van een telrij ontwikkelt zich in eerste instantie los van het
tellen van hoeveelheden. Een telrij kan foutloos opgezegd worden, maar bij
een-voor-een tellen gaat het toch fout.
Langzamerhand dringt het tot hen door dat het laatstgenoemde telwoord
ook de hoeveelheid aanduidt.
In deze fase krijgen kinderen ook de behoefte om hoeveelheden symbolisch
uit te beelden (ik ben 3 jaar en het kind steekt drie vingers op).
Groep 1 - 2: groeiend getalbegrip
Getallen kunnen verschillende functies hebben:
• Aantal
• Telgetal
• Meetgetal
• Naamgetal
• rekengetal
De verscheidenheid van tal-gedaanten kan tot grote verwarring leiden.
Aanvankelijk staan de verschillende getalaspecten nog betrekkelijk los van
elkaar. Geleidelijk verwerven ze elementair getalbegrip. Ze herkennen
verschillende functies van getallen in de dagelijkse werkelijkheid en leren
deze te onderscheiden en verbinden.
Ze doorzien steeds beter de overeenkomsten en verschillen tussen
nummeren, (af-)tellen en aantal bepalen.
Groep 1-2: groeiend getalbegrip
Kinderen leren kleine hoeveelheden te herkennen en tellen.
Ze kunnen een redelijk schatting maken
Ze kunnen getallen ordenen en vergelijken op meer, minder en evenveel.
Wat later kunnen ze eenvoudige erbij- en erafoperaties uitvoeren zonder de
voorwerpen erbij.
In deze ontwikkeling van elementair getalbegrip speelt tellen een cruciale rol.
Met name het handig en flexibel kunnen tellen van hoeveelheden in allerlei
situaties vormt voor een belangrijk deel de grondslag voor het aanvankelijk
rekenen.
Groep 1-2: leren tellen
Tellen:
• Akoestisch tellen
• Resultatief tellen
Tellen en rekenen zijn aanvankelijk in zoverre één, dat de eerste
rekenproblemen vooral tellend worden opgelost.
Het gaat dan in eerste instantie ook om het leren tellen. Tot 10 is
voldoende.
Zang-, tel- en bewegingsspelletjes zijn goed bruikbaar. Er is ritmische
ondersteuning en het aanbod is gevarieerd.
Probeer het tellen altijd in betekenisvolle situaties aan te bieden.
Bijvoorbeeld aftellen voor een spel.
Groep 1-2: leren tellen-en-rekenen
Het elementaire getalsbegrip ontwikkeld zich langs 3 niveaus:
• Context gebonden tellen-en-rekenen
• Objectgebonden tellen-en-rekenen
• Het pure tellen-en-rekenen
Om de overgang van het objectgebonden tellen-en-rekenen naar het pure
tellen-en-rekenen gemakkelijker te maken zijn bedekkingsopgaven erg
belangrijk.
Verder worden de stippenkaarten, die in de winkelhoek als prijsaanduiding
worden gebruikt uit die situatie gehaald en als op zich staand model
gehanteerd. De kinderen kunnen de koppeling met het winkeltje nog
maken. De context ‘winkel’ fungeert dan als model.
Groep 3(4): rekenen tot 20
Het rekenen tot 20 wordt in twee getalgebieden verdeeld:
• Rekenen tot 10
• Rekenen tot 20
In groep 3 zijn de volgende niveaus te onderscheiden:
• Tellend rekenen, waar nodig ondersteunt door telmateriaal
• Structurerend rekenen m.b.v. passende modellen
• Formeel rekenen met getallen als mentale objecten zonder
structuurmateriaal.
Groep 3(4): rekenen tot 20
In groep 3 kan niet meer volstaan worden met het pure tellen zoals dat in
groep 1 en 2 plaats heeft gevonden.
In groep 3 moet structuur in de getallenlijn tot 20 worden aangebracht.
De kralensnoer en de getallenlijn zijn goede hulpmiddelen, maar niet
voldoende om het doel (komen tot spontaan structureren en vervolgens
handig rekenen en memoriseren) te bereiken.
Het bereiken van voornoemd doel kan op 2 manieren:
• Ordenen volgens vijven
• Dubbelen
Groep 3(4): rekenen tot 20
Zeker in het begin is het belangrijk om getallen tot 20 in context aan te
bieden.
Geef getallen een gezicht. Op deze manier verwerven kinderen
referentiepunten, die ze bij het oplossen van contextopgaven moeten
gebruiken.
Kennis van betekenissen van getallen in contexten is een element van
basale gecijferdheid, dat vanaf het begin in het realistisch rekenonderwijs
betrokken moet worden.
Groep 3(4): rekenen tot 20
Naast de inhoud van de getallen (7 jaar enz.) dient ook de structuur van de
getallen aan bod te komen. Structurering maakt het immers mogelijk om
het tellend rekenen te overwinnen.
Bij de getallen tot 20 worden onderstaande structuurmodellen gebruikt:
• Lijnmodel
• Groepjesmodel (gewerkt met 1-5-10)
• Combinatiemodel (rekenrek; eierdoosjes;
getallentrein, 20-veld met 2 rijen van 10
Groep 3(4): rekenen tot 20
Van structurerend rekenen naar formeel rekenen.
Bij structurerend rekenen is de ll. nog handelend bezig op het rekenrek.
De volgende stap is dat het kind het eerste getal nog op de bovenste rij van
het rekenrek zet en het getal op de tweede rij er in gedachten bij zet.
Als derde stap kijkt het kind alleen nog maar naar het rekenrek.
Tenslotte is het rekenrek helemaal uit zicht.
Door die onthechting van het structuurmateriaal wordt de vrijheid en
flexibiliteit van de rekenhandelingen vergroot.
In alle fasen van manipulerend, kijken en denkend opereren speelt het
verwoorden van de rekenhandelingen een essentiële rol. Door te vertellen
wat je ziet, doet, denkt reflecteer je op je mentale handelen. Verwoorden
zorgt voor niveauverhoging.
Groep 3(4): rekenen tot 20
Het verwoorden van rekenhandelingen kan gekoppeld worden aan het
noteren van die operaties in rekentaal.
Een voorbeeld hiervan is de pijlentaal, die ontwikkeld is als schematisering
van de busopgaven.
Opgaven als 6+7 kunnen op verschillende manieren uitgerekend worden.
Maar het splitsen bij de tien moet zeker onder de aandacht van de kinderen
gebracht worden, omdat deze methode bij het rekenen tot de 100 veel
perspectief biedt.
Groep 3(4): rekenen tot 20
Een belangrijke didactische taak van de lkr. is het verzorgen van
oefenprogramma’s.
Er zijn twee verschillende vormen van oefenen te onderscheiden:
• Gericht oefenen
• Productief oefenen
Twee rekenstrategieën voor optellen en aftrekken hebben speciale
aandacht:
• De sprong via tien (13-5
13-3=10
10-2=8
• De tiensprong 13-10 direct als 13-10 18-12 18-10=8 8-2=6
Groep 4: rekenen tot 100
De niveaus van rekenen in groep 4 komen overeen met die in groep 3, maar
dat binnen het domein ‘tot 100’.
Nieuw in groep 4 zijn de beschrijvingen van de basisoperaties
vermenigvuldigen en delen.
Groep 4: rekenen tot 100
Leren tellen
Sommige kinderen leren de getallenrij tot 100 spelenderwijs.
Anderen moeten het gericht aangeboden krijgen.
Het beste is om eerst de grote telrij van de tienen inprenten en dan pas de
grote getallenrij tot 100 systematisch oefenen.
Het opzeggen en het noteren moet bij voorkeur aan elkaar gekoppeld zijn.
Zeggen ‘een en twintig’ en schrijven 21.
Bij het leren tellen tot 100 zijn nog twee belangrijke obstakels:
• Overschrijding van het tiental
• terugtellen
Groep 4: rekenen tot 100
Kinderen die sommen als 48+29=.. tellend proberen op te lossen, merken al
snel dat het onbegonnen werk is.
48..49..50..51.. Je telt en je moet bijhouden hoeveel je er al bijgedaan
hebt. Ze gaan dan ook al snel naar verkortingen zoeken.
Bij structurerend rekenen maken de kinderen bij deze opgave gebruik van
de sprong over de tien of de tiensprong. Ze maken gebruik van een lege
getallenrij of een ander materiaal.
Bij formeel rekenen hebben de kinderen de hulpmiddelen niet meer nodig.
Ze rekenen de opgave in hun hoofd uit. Soms noteren ze nog de tussenstapjes.
Groep 4: rekenen tot 100
Vermenigvuldigen en delen zijn even elementair als optellen en aftrekken.
In het begin noteren de kinderen de handelingen als herhaald optellen of
aftrekken. Maar in de loop van groep 4 worden die vervangen door x en :
In de mechanische rekendidactiek begon op dat moment het inslijpen van
de tafels.
Eerst die van 2, 10 en 5. Daarna de rest.
Op deze manier zien kinderen vaak niet dat 3x7 ook uitgerekend kan worden
als 7x3.
Dat belemmerd de toepasbaarheid en het verkrijgen van inzicht in de
bewerking.
Groep 4: rekenen tot 100
In de realistische rekendidactiek worden vermenigvuldigen en delen niet
strikt aan het leren van tafels gebonden. Eerst vindt er een langdurige
periode van begripsvorming plaats.
Wanneer we beginnen met vermenigvuldigen is het belangrijk dat het begrip
‘keer’ met ‘herhaald erbij’ wordt verbonden.
Modellen verbonden aan contextopgaven zijn erg belangrijk voor het leren
vermenigvuldigen.
Er wordt van tellend vermenigvuldigen gesproken wanneer de ll. De som
oplost door middel van herhaald optellen.
Bij structurerend vermenigvuldigen wordt niet meer herhaald opgeteld,
maar wel gebruik gemaakt van modellen. Rechthoekpatronen zijn erg
bruikbaar.
Bij formeel vermenigvuldigen worden geen modellen meer gebruikt, maar maakt men
gebruik van verwisseleigenschappen 4x7/7x4, dubbellen, een maal meer/minder.. )
Groep 4: rekenen tot 100
Modellen voor structurerend vermenigvuldigen
Groep 4: rekenen tot 100
Informeel delen
Dele kan gezien worden als herhaald aftrekken. Na uitgebreide verkenning
van vermenigvuldigen is het delen in verkorte vorm omgekeerd
vermenigvuldigen.
Er zijn twee soorten van delen:
• Opdelen (48 sterren in rechthoek met 8 sterren per rij. Hoeveel rijen zijn er?)
• Verdelen (48 sterren in rechthoek in 8 gelijke rijen. Hoeveel sterren per rij?)
Door de symmetrie van het rechthoekpatroon zien we deze problemen als
identiek. Het onderscheid tussen verdelen en opdelen valt hier eigenlijk weg.
Kinderen worden met dit onderscheid niet lastig gevallen.
Groep 4: rekenen tot 100
Oefenvormen x en :
-
Bingo
-
Tafeldictee
-
Geheimschriften
-
Inkleuren vlakken met sommen
-
Tabelopgaven
-
Op honderdveld veelvouden van 2, 3 enz. doorstrepen
Overzicht niveaus groep 1 t/m 4
groep
1-2
Context-gebonden tellen en rekenen
Tellen in betekenisvolle situaties: Tellen bij een gezelschapsspel; winkeltje met prijzen
als stippen weergegeven; hoeveel kinderen in het groepje enz
1-2
Object-gebonden tellen en rekenen
Hoeveel blokjes liggen er onder het doek? Je haalt er een weg. Hoeveel blokjes liggen er
nu. Hier staan 7 brandende kaarsjes. Ik blaas er 3 uit. Hoeveel kaarsjes branden nog.
1-2
Pure tellen en rekenen
7 eraf 3 kan uitgerekend worden met tellen op vinger. Vingers/ streepjes zijn
representaties van het getal. Koppeling tussen telbare representatie en
cijfersymbool (bijv. 1 kant kaartje stippen en andere kant het bijbehorende cijfer)
3
Tellend rekenen tot 20
Bussituatie: er zitten 8 mensen in de bus. Er stappen er 5 uit. Hoeveel mensen zitten er
nog in de bus. In eerste instantie worden deze opgaven op de vinger uitgerekend.
3
Structurerend rekenen tot 20
Met behulp van structureermateriaal, waarin de 5 besloten ligt, wordt het vingerrekenen
omgevormd tot structurerend rekenen. Hierbij wordt dubbelen en vijven met de vingers
nagebootst. Rekenrek is een structuurmodel.
3
Formeel rekenen tot 20
Kinderen kunnen op een flexibele wijze met getallen opereren zonder steun van
structuurmodellen. Ze beschikken over heel wat gememoriseerde rekenfeiten en kunnen
daarmee andere opgaven handig uitrekenen. Ze zien in busopgaven als 8 eruit 5 direct de
bijbehorende splitsing.
4
Tellend rekenen tot 100
48+29= kinderen tellen door 48..49..50..51
4
Structurerend rekenen tot 100
Splitsen en aanvullen tot tiental/ tiensprong op bijv. lege getallenlijn
4
Formeel rekenen tot 100
Kinderen gaan de opgaven verkorten en hebben geen lege getallenlijn meer nodig. Ze
kunnen nog wel een tussenstap van een bewerking even noteren
leerstofdomein hele getallen