UItwerkingen Meetkunde MULO-A 1950 Rooms Katholiek

Uitwerkingen Meetkunde MULO-A 1950 Rooms Katholiek
Opgave 1
DCP  BCP (diagonaal in ruit halveert hoek) 

1) DPC  BPC ( SC is symmetrie-as)
  CDP  CPB (zhh)

CD  BC (ruit)

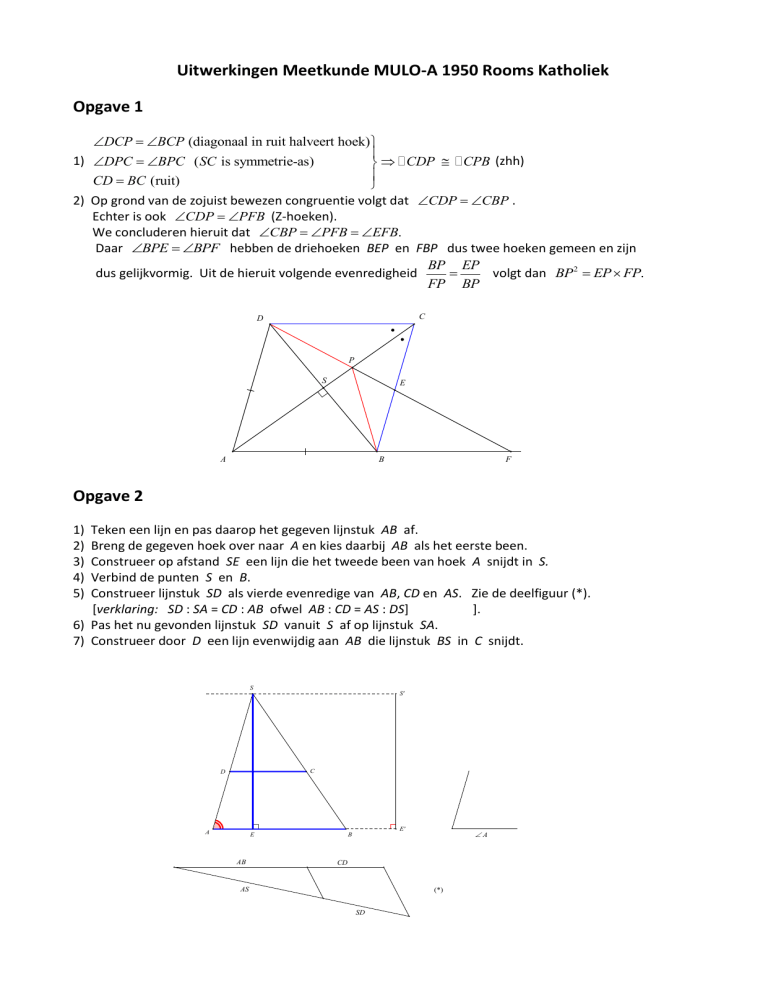
2) Op grond van de zojuist bewezen congruentie volgt dat CDP  CBP .
Echter is ook CDP  PFB (Z-hoeken).
We concluderen hieruit dat CBP  PFB  EFB.
Daar BPE  BPF hebben de driehoeken BEP en FBP dus twee hoeken gemeen en zijn
BP EP
dus gelijkvormig. Uit de hieruit volgende evenredigheid
volgt dan BP2  EP  FP.

FP BP
C
D
P
S
E
A
B
F
Opgave 2
1)
2)
3)
4)
5)
Teken een lijn en pas daarop het gegeven lijnstuk AB af.
Breng de gegeven hoek over naar A en kies daarbij AB als het eerste been.
Construeer op afstand SE een lijn die het tweede been van hoek A snijdt in S.
Verbind de punten S en B.
Construeer lijnstuk SD als vierde evenredige van AB, CD en AS. Zie de deelfiguur (*).
[verklaring: SD : SA = CD : AB ofwel AB : CD = AS : DS]
].
6) Pas het nu gevonden lijnstuk SD vanuit S af op lijnstuk SA.
7) Construeer door D een lijn evenwijdig aan AB die lijnstuk BS in C snijdt.
S
S'
C
D
E'
A
E
AB
A
B
CD
AS
(*)
SD
Opgave 3
1) Volgens de machtstelling geldt CD2  CA  CB en dus 102  5  (5  2r ) waaruit volgt r  7,5.
2) De zijden van driehoek CDM zijn nu bekend, namelijk CM = 12,5 en CD = 10 en MD = 7,5.
Driehoek CBE is gelijkvormig met driehoek CMD daar ze een rechte hoek en C gemeen hebben.
20 8
 keer zo groot als CM.
Zijde CB van driehoek CBE is gelijk aan 20 en is dus
12,5 5
8
8
1
8
8
Vanwege de gelijkvormigheid is dus BE   MD   7  12 en CE   CD   10  16.
5
5
2
5
5
Het gevolg is dat DE  CE  CD  16  10  6.
We gebruiken nogmaals de machtstelling: ED2  EF  EB ofwel 62  EF 12 zodat EF  3 .
De stelling van Pythagoras voor driehoek DEF geeft dan ten slotte DF 2  DE 2  EF 2  62  32  45
waaruit volgt DF  45  3 5.
E
F
D
10
C
5
r
A
r
M
r
B