Uitwerkingen Meetkunde Mulo-B 1950

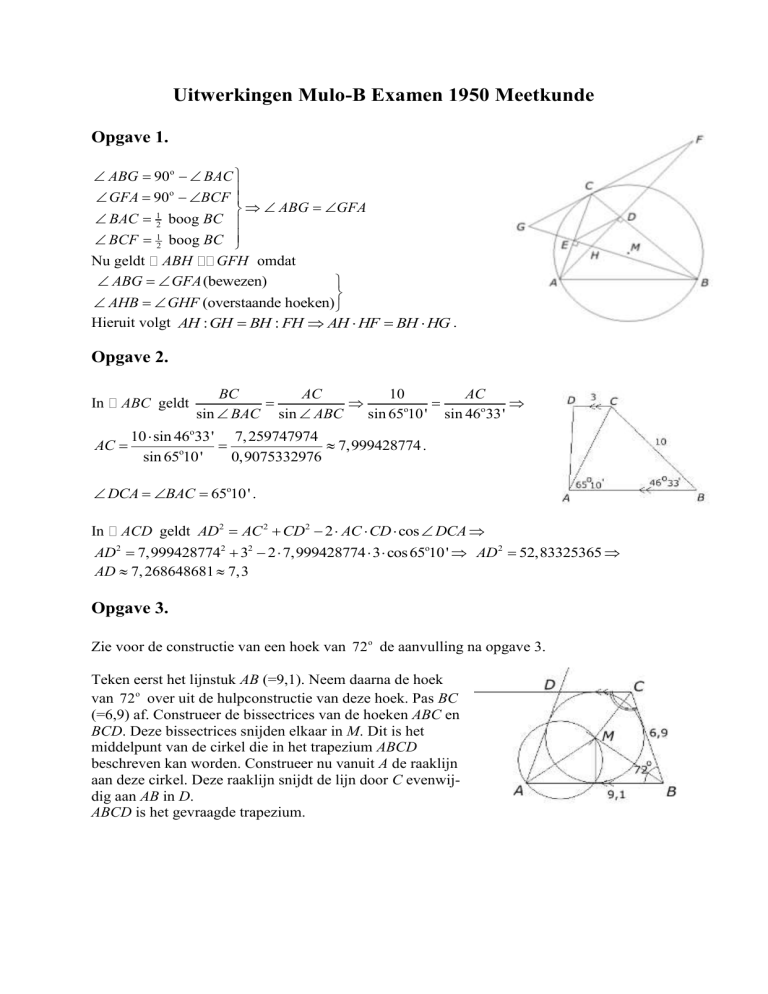
Uitwerkingen Mulo-B Examen 1950 Meetkunde
Opgave 1.
 ABG  90o   BAC 

 GFA  90o  BCF 
   ABG  GFA
 BAC  12 boog BC 
 BCF  12 boog BC 
GFH omdat
Nu geldt ABH
 ABG   GFA (bewezen)


 AHB   GHF (overstaande hoeken) 
Hieruit volgt AH : GH  BH : FH  AH  HF  BH  HG .
Opgave 2.
In
ABC geldt
AC 
BC
AC
10
AC




o
sin  BAC sin  ABC
sin 65 10 ' sin 46o33'
10  sin 46o33' 7, 259747974

 7,999428774 .
sin 65o10'
0,9075332976
 DCA  BAC  65o10' .
In
ACD geldt AD2  AC 2  CD2  2  AC  CD  cos  DCA 
AD2  7,9994287742  32  2  7,999428774  3  cos 65o10'  AD2  52,83325365 
AD  7, 268648681  7,3
Opgave 3.
Zie voor de constructie van een hoek van 72 o de aanvulling na opgave 3.
Teken eerst het lijnstuk AB (=9,1). Neem daarna de hoek
van 72 o over uit de hulpconstructie van deze hoek. Pas BC
(=6,9) af. Construeer de bissectrices van de hoeken ABC en
BCD. Deze bissectrices snijden elkaar in M. Dit is het
middelpunt van de cirkel die in het trapezium ABCD
beschreven kan worden. Construeer nu vanuit A de raaklijn
aan deze cirkel. Deze raaklijn snijdt de lijn door C evenwijdig aan AB in D.
ABCD is het gevraagde trapezium.
Verdeling van een lijnstuk in uiterste en middelste reden en constructie hoek van
72o .
figuur 1
Voor deze constructie gaan we uit van ABC met  ABC  90o en AB  2  BC .
Construeer een cirkel met middelpunt C en straal BC. Deze snijdt zijde AC in D.
Construeer nu een cirkel met middelpunt A en straal AD. Deze snijdt zijde AB in E.
We hebben nu een gulden snede aangebracht op lijnstuk AB, d.w.z. het grootste deel AE is
middelevenredig tussen het kleinste lijnstuk AE en het gehele lijnstuk AB. Zie figuur 1.
Gaan we uit van BC  1  ( AB  2  AC  5) . Als nu ook geldt CD  1 dan geldt verder
AE  AD  5  1 dus BE  2  ( 5  1)  3  5
Er geldt dus BE : AE  AE : AB of (3  5) : ( 5  1)  ( 5  1) : 2 .
Ook zeggen we, da het lijnstuk AB in uiterste en middelste reden is verdeeld. Eigenlijk een
vreemde uitdrukking, want er zijn twee reden ( BE : AB en AE : AB ), die men eventueel
beide uiterste reden zou kunnen noemen, maar een middelste reden is er niet want er zijn maar
twee reden.
Voorheen sprak men over een lijnstuk in gedurige reden verdelen. Een gedurige reden is een
evenredigheid, waarbij beide middelste termen gelijk zijn.
Door nu het kleinste gedeelte van AB, nl. BE te gebruiken als basis van een
gelijkbenige driehoek met als benen het grootste stuk van AB, nl AE, krijgen
we een driehoek met  B   E  72o en  A  36o . Zie figuur 2.
figuur 2
figuur 3
In figuur zien we nogmaals de constructie van
de verdeling in uiterste en middelste reden.
Daar is de constructie van een driehoek van één hoek
van 36o en twee hoeken van 72 o aan toegevoegd.
In ABB ' geldt, dat AE  AB '  5  1 en
B ' E  BE  3  5  EF 
3 5
 1 12  12 5 .
2
EF 1 12  12 5


AF
5 1
Duidelijk is nu dat  AEB '  AB ' E  72o .
In
AEF geldt sin  EAF 
1
4
5  14   EAF  18o   EAB '  36o .