Mathematica Referentiekaart

Mathematica Referentiekaart1
André Heck
c 1999, Amstel Instituut
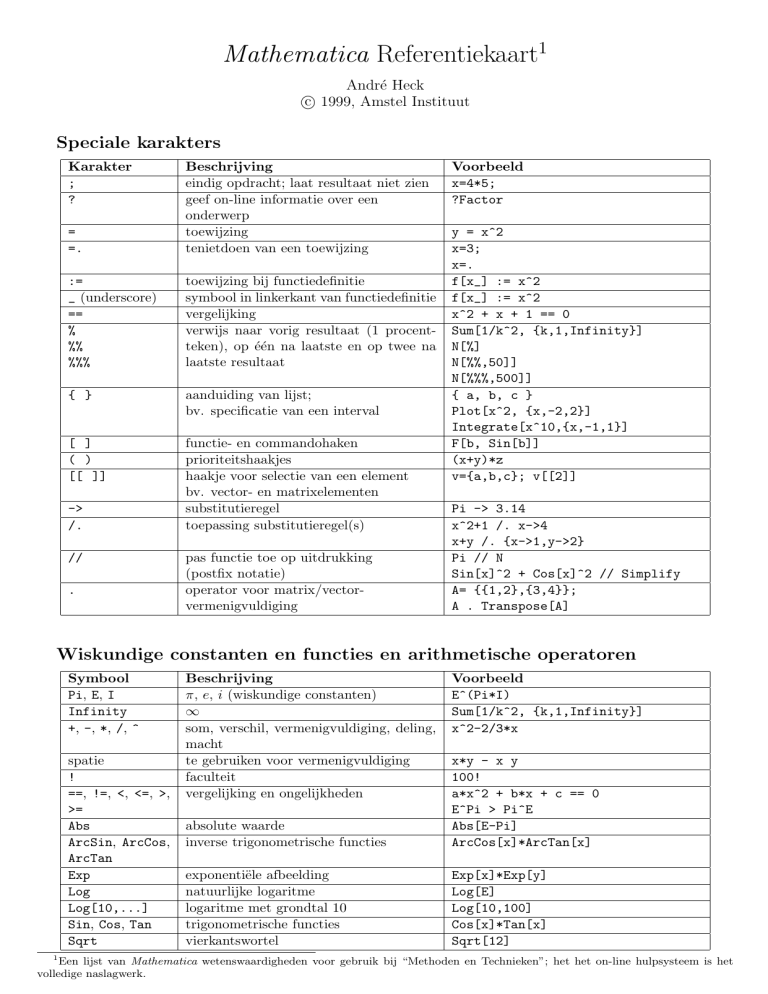
Speciale karakters
Karakter
;
?
=
=.
Beschrijving
eindig opdracht; laat resultaat niet zien
geef on-line informatie over een
onderwerp
toewijzing
tenietdoen van een toewijzing
:=
_ (underscore)
==
%
%%
%%%
toewijzing bij functiedefinitie
symbool in linkerkant van functiedefinitie
vergelijking
verwijs naar vorig resultaat (1 procentteken), op één na laatste en op twee na
laatste resultaat
{ }
aanduiding van lijst;
bv. specificatie van een interval
[ ]
( )
[[ ]]
functie- en commandohaken
prioriteitshaakjes
haakje voor selectie van een element
bv. vector- en matrixelementen
substitutieregel
toepassing substitutieregel(s)
->
/.
//
.
pas functie toe op uitdrukking
(postfix notatie)
operator voor matrix/vectorvermenigvuldiging
Voorbeeld
x=4*5;
?Factor
y = x^2
x=3;
x=.
f[x_] := x^2
f[x_] := x^2
x^2 + x + 1 == 0
Sum[1/k^2, {k,1,Infinity}]
N[%]
N[%%,50]]
N[%%%,500]]
{ a, b, c }
Plot[x^2, {x,-2,2}]
Integrate[x^10,{x,-1,1}]
F[b, Sin[b]]
(x+y)*z
v={a,b,c}; v[[2]]
Pi -> 3.14
x^2+1 /. x->4
x+y /. {x->1,y->2}
Pi // N
Sin[x]^2 + Cos[x]^2 // Simplify
A= {{1,2},{3,4}};
A . Transpose[A]
Wiskundige constanten en functies en arithmetische operatoren
Symbool
Pi, E, I
Infinity
+, -, *, /, ^
spatie
!
==, !=, <, <=, >,
>=
Abs
ArcSin, ArcCos,
ArcTan
Exp
Log
Log[10,...]
Sin, Cos, Tan
Sqrt
Beschrijving
π, e, i (wiskundige constanten)
∞
som, verschil, vermenigvuldiging, deling,
macht
te gebruiken voor vermenigvuldiging
faculteit
vergelijking en ongelijkheden
Voorbeeld
E^(Pi*I)
Sum[1/k^2, {k,1,Infinity}]
x^2-2/3*x
absolute waarde
inverse trigonometrische functies
x*y - x y
100!
a*x^2 + b*x + c == 0
E^Pi > Pi^E
Abs[E-Pi]
ArcCos[x]*ArcTan[x]
exponentiële afbeelding
natuurlijke logaritme
logaritme met grondtal 10
trigonometrische functies
vierkantswortel
Exp[x]*Exp[y]
Log[E]
Log[10,100]
Cos[x]*Tan[x]
Sqrt[12]
1
Een lijst van Mathematica wetenswaardigheden voor gebruik bij “Methoden en Technieken”; het het on-line hulpsysteem is het
volledige naslagwerk.
Nuttige opdrachten
Opdracht
Chop
N
Remove
Round
Table
<<
>>
Beschrijving
vervang kleine getallen door nul
reken m.b.v. kommagetallen
verwijder toewijzingen
bv. begin met schone lei
rond af op gehele getallen
maak een lijst
laad een Mathematica pakket of
lees een bestand
schrijf resultaat naar bestand
Voorbeeld
Chop[1.2 10^(-17)]
{N[Pi], N[Pi,50]}
Remove["Global‘*"]
Round[1.7]
Table[i^2, {i,1,10}]
<<Statistics‘
Table[i^2,{i,1,10}] >> kwadraten
Manipulatie van uitdrukkingen
Opdracht
First
Flatten
Last
Length
Part
Beschrijving
eerste onderdeel van uitdrukking
bv. linkerkant van (on)gelijkheid
haal (overtollige) accolades weg
laatste onderdeel van uitdrukking
bv. rechterkant van (on)gelijkheid
aantal termen in een uitdrukking
selecteer term(en) van een uitdrukking
Voorbeeld
First[Tan[x] == x^2]
First[{a,b,c}]
Flatten[{{1,2},{3,4}}]
Last[Tan[x] == x^2]
Last[{a,b,c}]
Length[1+x+x^2]
Part[{1,x,x^2}, 2]
Vereenvoudiging
Opdracht
Expand
Factor
PowerExpand
Simplify
TrigExpand
TrigReduce
Together
Beschrijving
werk een uitdrukking uit
ontbind in factoren
werk een uitdrukking met machten uit
vereenvoudig een uitdrukking
werk een trigonometrische uitdrukking
uit
vereenvoudig
een
trigonometrische
uitdrukking
breng onder een noemer
Voorbeeld
Expand[(x+1)^2]
Factor[x^2-2x+1]
PowerExpand[Sqrt[x^2y]]
Simplify[Cos[x]^2+Sin[x]^2]
TrigExpand[Sin[2x]]
TrigReduce[Cos[x]^2-Sin[x]^2]
Together[x + 1/x]
Lineaire Algebra
Opdracht
Beschrijving
de matrix in onderstaande voorbeelden is
.
Det
Eigensystem
Eigenvalues
Eigenvectors
IdentityMatrix
Inverse
MatrixForm
MatrixPower
Outer
Table
matrixvermenigvuldiging
bereken de determinant
bereken eigenwaarden en eigenvectoren
bereken de eigenwaarde(s)
bereken de eigenvector(en)
maak identiteitsmatrix
bepaal de inverse matrix
toon in matrix-gedaante
machtsverheffen van matrices
nuttig voor berekenen van Jacobiaan
maak een matrix of vector
Voorbeeld
A = {{-2, 2, 3},
{ 3, 7,-8},
{10,-4,-3}}
A . Transpose[A]
Det[A]
Eigensystem[A]
Eigenvalues[A]
Eigenvectors[A]
IdentityMatrix[4]
Inverse[A]
MatrixForm[A]
MatrixPower[A,10]
Outer[D, {x^2*y,x*y}, {x,y}]
Table[GCD[i,j], {i,1,6}, {j,1,6}]
Calculus
Opdracht
D
DSolve
FindRoot
Integrate
Limit
PhasePlot
Series
Solve
Sum
VisualDSolve
Beschrijving
vaak beginnen met2
bereken de (partiële) afgeleide
los gewone differentiaalvergelijking(en)
op
los vergelijking numeriek op
bereken een onbepaalde of bepaalde
integraal
bereken een limit
maak een faseportret en teken oplossingskrommen van een stelsel van gewone
differentiaalvergelijkingen
bepaal een reeksontwikkeling van een
functie om een gegeven punt
los de vergelijking(en) of ongelijkheid op
voer sommatie uit
teken oplossingskrommen van een gewone
differentiaalvergelijking met beginvoorwaarden
Voorbeeld
<<VisualDSolve‘
D[Exp[x*y^2], x, {y,2}]
DSolve[y’[x] == a*y[x], y[x], x]
FindRoot[Cos[x] == x, {x,1}]
Integrate[x/(x^3+1), x]
Integrate[1/(Sin[x]^2+1), {x,0,2Pi}]
Limit[Sin[x]/x, x->0]
odes = {q’[t]==p[t], p’[t]==-q[t]};
PhasePlot[odes, {p[t],q[t]},
{t,0,8}, {p,-1,1}, {q,-1,1},
InitialValues -> {0,0,0.9},
VectorField -> True]
Series[Sin[x], {x,0,20}]
Solve[a*x^2 + b*x + c == 0, x]
Sum[1/k^2, {k,1,Infinity}]
VisualDSolve[u’[t]+Sin[u[t]]==0,
{t,0,5}, {u,-1,1},
DirectionField -> True,
InitialValues -> {0,0.7}]
Grafiek
Opdracht
ListPlot
Beschrijving
teken een lijst van waarden
ParamtericPlot
teken een geparametriseerde
kromme
teken een geparametriseerd
oppervlak
ParamtericPlot3D
Plot
maak een 2-dimensionale grafiek
van functies
Plot3D
maak een 3-dimensionale grafiek
van een functie
teken meerdere plaatjes in één
figuur of toon grafiek met andere
opties
Show
Voorbeeld
ListPlot[{1,9,4,16,36,25},
PlotStyle->PointSize[0.03]];
ParametricPlot[{Cos[t],Sin[t]},
{t,0,2Pi}, AspectRatio->1];
ParametricPlot3D[{r*Cos[t],r*Sin[t],t},
{r,0,1},{t,0,6*Pi},
PlotPoints->{2,80}];
Plot[(x+1)^2*Sin[x], {x,0,2Pi}];
Plot[{Cos(x), Sin[x]}, {x,0,2Pi},
PlotStyle -> {{Thickness[0.005]},
{Thickness[0.025]}}];
Plot3D[Sin[x*y], {x,-3,3}, {y,-3,3}];
Plot[Cos[x], {x,0,2Pi},
PlotStyle->RGBColor[1,0,0]];
Plot[Sin[x], {x,0,2Pi},
PlotStyle->RGBColor[0,1,0]];
Show[{%,%%}];
Show[%, PlotLabel-> "2 curves"];
Statistiek (stats pakket)
Opdracht
CDF[NormalDistribution[0,1]]
CDF[LaplaceDistribution[0,1]]
Fit
Beschrijving
altijd beginnen met:
cumulatieve dichtheidsfunctie van normale
verdeling met gemiddelde 0 en standaarddeviatie 1
cumulatieve dichtheidsfunctie van standaard
Laplace verdeling
bepaal kleinste kwadraten benadering
bereken de gemiddelde
waarde
Median
bereken de mediaan
Random[LaplaceDistribution[0,1]] genereer random getal
in standaard Laplace
verdeling
Random[NormalDistribution[0,1]] genereer random getal
in standaard normale
verdeling
Random[UniformDistribution[0,1]] genereer random getal
in standaard uniforme
verdeling
ListPlot
teken een spreidingsdiagram
mean
StandardDeviation
Variance
bereken de standaardafwijking
bereken de variantie
Voorbeeld
<<Statistics‘
Plot[CDF[
NormalDistribution[0,1]][x],
{x,-4,4}]
Plot[CDF[
LaplaceDistribution[0,1]][x],
{x,-4,4}]
data = {{1,1}, {2,4.5}, {3,9.2},
{4,15.5}};
Fit[data, {1,x,x^2}, x]
Mean[{1,2,3,4,5,6}]
Median[{1,2,4,5,6}]
Random[NormalDistribution[0,1]]
Table[Random[
NormalDistribution[0,1]],{8}]
Random[UniformDistribution[0,1]]
data = {{1,1}, {2,2.5}, {3,3.2},
{4,4}};
ListPlot[data,
PlotStyle->PointSize[0.04]];
StandardDeviation[{1,2,3,4,5,6}]
Variance[{1,2,3,4,5,6}]
Iteratie
Opdracht
Nest
NestList
FixedPoint
FixedPointList
Beschrijving
pas een functie een aantal
malen toe
pas een functie een aantal malen toe
en bewaar tussenresultaten in een
lijst
pas een functie herhaald toe tot geen
verandering meer optreedt
pas een functie herhaald toe tot geen
verandering meer optreedt en bewaar tussenresultaten in een lijst
Voorbeeld
f[x_] := 2x;
Nest[f,1,10]
f[x_] := 2x;
NestList[f,1,10]
f[x_] := 1/2*x + 1/x;
FixedPoint[f,1.0]
f[x_] := 1/2*x + 1/x;
FixedPointList[f,1.0]