fysica vijfde jaar.

Evalueren in 5-de jaar fysica blz.1
1 KINEMATICA
1 Meerkeuze
1.1 Een jogger loopt 12 km in 1 uur. Om de 2 km kijkt hij op zijn uurwerk en merkt dat
hij telkens 10 minuten nodig heeft om die afstand te lopen. Welke uitspraak is juist?
• De beweging van de jogger is een eenparig rechtlijnige beweging.
• De beweging van de jogger is eenparig maar niet noodzakelijk rechtlijnig.
• De beweging van de jogger is geen eenparig rechtlijnige beweging.
• De beweging van de jogger is rechtlijnig maar niet noodzakelijk eenparig.
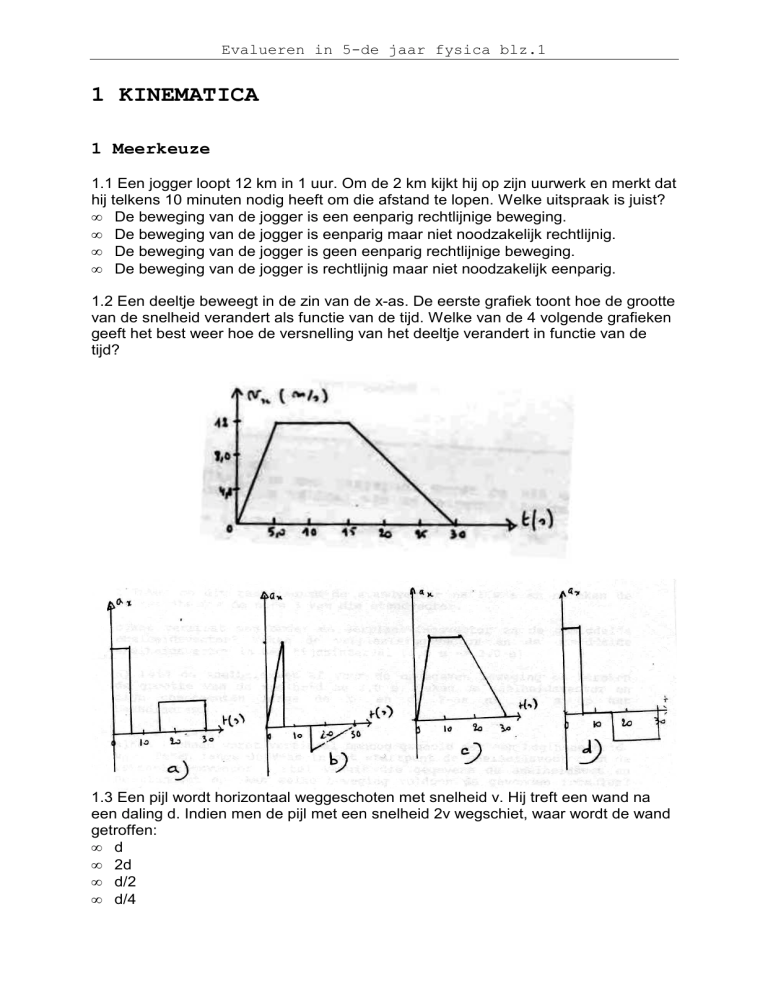
1.2 Een deeltje beweegt in de zin van de x-as. De eerste grafiek toont hoe de grootte
van de snelheid verandert als functie van de tijd. Welke van de 4 volgende grafieken
geeft het best weer hoe de versnelling van het deeltje verandert in functie van de
tijd?
1.3 Een pijl wordt horizontaal weggeschoten met snelheid v. Hij treft een wand na
een daling d. Indien men de pijl met een snelheid 2v wegschiet, waar wordt de wand
getroffen:
• d
• 2d
• d/2
• d/4
Evalueren in 5-de jaar fysica blz.2
1.4 Op een platte spoorwagen van een met constante snelheid voorbijrijdende
goederentrein staat een jongleur die telkens een balletje verticaal omhoog gooit. Wat
is de baan die een toeschouwer, die op de spoorwegberm toekijkt, het balletje ziet
volgen? Leg uit.
1.5 Als een lichaam overeenkomstig deze grafiek beweegt, dan is de snelheid op de
vijfde seconde:
•
•
•
•
120 m/s
100 m/s
70 m/s
0,50 m/s.
1.6 Bij de paardjes op een kermismolen hebben de binnenste:
een grotere / kleinere / gelijke hoeksnelheid
een grotere / kleinere / gelijke baansnelheid
dan de buitenste.
1.7 Iemand heeft een proef uitgevoerd over een EVRB. Als resultaat gaf hij volgende
grafiek die de plaatsfunctie van de bewegende massa weergeeft. Welke grootheid
moet er in de horizontale as staan?
• t(s)
Evalueren in 5-de jaar fysica blz.3
•
•
•
t² (s²)
t1/2 (s1/2)
1/t (1/s)
2 Juist of fout
2.1 Een puntmassa beweegt volgens de plaatsfunctie:
x = 2t² - 6t + 7 De eenheid van x is m. Deze beweging is eenparig vertraagd voor t
< 1,5 s
2.2 Wanneer een lichaam in rust een versnelling van 2 m/s2 krijgt, dan zal:
• de snelheid van dit lichaam na 5 s 5 maal zo groot zijn als na 1 s.
• de snelheid van dit lichaam elke seconde met 2 m/s toenemen.
• de snelheid van dit lichaam elke seconde met 2 m/s toe- of afnemen.
• dat lichaam in de eerste 2 seconde 2 m afleggen.
2.3 Bij een eenparig vertraagde rechtlijnige beweging is de snelheidsverandering
tijdens de volgende seconde steeds kleiner dan in de voorgaande.
2.4 De beweging van een star lichaam kan altijd volledig bestudeerd worden door het
lichaam te herleiden tot een massapunt en dan hiervan de beweging te bestuderen.
3 Reproductie
3.1 Stel de bewegingsvergelijkingen op voor een horizontale worp. Leid hieruit de
baanvergelijking af.
Hoe bereken je de grootte van de snelheid op een bepaald tijdstip.
r
3.2 Een kogel wordt met snelheid vO onder een hoek α0 weggeschoten. Stel deze
toestand voor op een figuur. Stel de formules op waarmee men het bereik en de
maximale hoogte van een schuine worp berekent.
3.3 Leid de baanvergelijking af (een formule) bij een schuine worp.
3.4 Bewijs dat bij een eenparig cirkelvormige beweging de versnelling
middelpuntzoekend is.
Evalueren in 5-de jaar fysica blz.4
4 Grafieken interpreteren / opstellen
4.1 Een deeltje beschrijft een ééndimensionale beweging op een X-as. De positie als
functie van de tijd is weergegeven door de onderstaande grafiek
x (m)
120
100
80
60
40
20
0
0
5
10
15
20
25
t (s)
Op welk ogenblik is de ogenblikkelijke snelheid 0 m/s?
Bereken de beginsnelheid. Teken hieronder de overeenkomstige vx(t)- grafiek.
t (s)
4.2 Teken de vx(t)-grafiek van een fietser die de volgende beweging uitvoert:
een fietser vertrekt vanuit rust en voert de eerste 40 s zijn snelheid eenparig op tot 30
km/h. Hij rijdt de volgende 3,0 minuten verder met deze snelheid. Vervolgens komt
hij met een constante versnelling in 20 s tot stilstand.
Teken de overeenkomstige ax(t)-grafiek.
4.3 Een automobilist (A) rijdt op een weg waar een snelheidsbeperking van 30 km/h
geldt. Hij rijdt te snel voorbij een controlepatrouille van de politie (P), die de
achtervolging inzet 5,0 s na het passeren van de automobilist.
Hieronder vind je de x(t)-grafiek die beide bewegingen voorstelt.
Evalueren in 5-de jaar fysica blz.5
700
x (m)
600
500
400
300
A
200
P
100
0
t (s)
0
5
10
15
20
25
30
35
Bereken m.b.v. de gegevens uit de grafiek de snelheid van de automobilist in km/h.
Bepaal (uit de grafiek) de afstand die de politie moet afleggen om de automobilist in
te halen.
Bereken m.b.v. de gegevens uit de grafiek de versnelling van de politie. De beweging
is eenparig versneld.
4.4 Een balletje wordt met beginsnelheid 10 m/s horizontaal weggeschoten op een
hoogte van 100 m.
Teken na de nodige berekeningen (1 punt elke 0,50 s) de baan gedurende 4,0 s.
Teken in dezelfde grafiek, maar in een andere kleur de snelheidsvectoren (na de
nodige berekeningen), elke 1,0 s.
4.5 Met een tikker wordt om de 0,020 s een afdruk gezet op een bewegende
papierstrook. Volgende onderlinge afstanden tussen 2 punten worden gemeten in
mm vanaf een goed duidelijk te onder scheiden punt: 11,0 / 13,9 / 16,3/ 20,6 / 23,6 /
27,5 / 31,2 / 34,3 / 37,3 / 41,6 / 45,8 / 47,9 / 52,9.
Maak een tabel, bereken de snelheid en zet uit in een v(t)-grafiek. Leid uit de grafiek
de gemiddelde versnelling af.
Zoek uit de grafiek het begintijdstip van de beweging (rust).
Hoe lang duurt de beweging? Welke weg werd er afgelegd?
4.6 De bewegingen van een fietser, een voetganger en een automobilist zijn
voorgesteld op onderstaande grafieken.
Evalueren in 5-de jaar fysica blz.6
Duid bij elke grafiek aan over welke weggebruiker het gaat.
a)……………….
b)……………….
c)……………….
Motiveer je antwoord.
4.7 Een automobilist A rijdt op een weg. Voor deze weg geldt een maximumsnelheid
van 30 km/h. Op een bepaald punt van deze weg controleert de politie de snelheid.
De automobilist blijkt sneller te rijden dan 30 km/h. Een motoragent M zet 5
seconden na het passeren van de automobilist de achtervolging in. In onderstaande
grafiek staat zowel van de automobilist A als van de motoragent M de afgelegde weg
als functie van de tijd weergegeven. Als begintijd is genomen het moment waarop de
automobilist het controlepunt passeert.
Bereken met behulp van de gegevens uit de grafiek de snelheid van de automobilist
A in km/h.
Leg uit waarom de grafiek die de beweging van M voorstelt, de eerste 5 seconden
samenvalt met de horizontale as.
Bepaal hoeveel meter de agent heeft afgelegd op het moment dat hij de automobilist
voorbij rijdt.
Bereken met behulp van gegevens uit de grafiek de versnelling van de motoragent
M. De beweging van de motoragent kan als eenparig versneld worden beschouwd.
Evalueren in 5-de jaar fysica blz.7
In de grafieken is verondersteld dat zowel A en M hun beweging verder zetten.
In werkelijkheid geeft de agent een stopteken als hij naast de automobilist is
gekomen. Beiden beginnen tegelijkertijd te remmen (eenparig vertraagd) en komen
tegelijkertijd tot stilstand.
Welk van onderstaande v(t)-grafieken geeft het best de beweging van beide
voertuigen weer?
Komen beide op dezelfde plaats tot stilstand? Verklaar.
4.8 Schets een x(t)- en een v(t)-grafiek van volgende beweging: een voorwerp wordt
van op de grond verticaal omhoog geworpen en valt na een paar ogenblikken terug
op de grond.
4.9 Van een ééndimensionale beweging is de ax(t)-grafiek getekend. Teken van deze
beweging de bijhorende vx(t)- grafiek. Verklaar je redenering als je weet dat je vanuit
rust vertrekt.
Evalueren in 5-de jaar fysica blz.8
5 Rekenvragen
5.1 Een autobestuurder rijdt met een constante snelheid van 25,0 m/s. Plotseling ziet
hij de verkeerslichten rood worden. Hij heeft 0,800 s nodig om de remmen in werking
te brengen en remt dan af met een constante versnelling van 5,0 m/s².
Na hoeveel meter komt het voertuig tot stilstand?
Teken de overeenkomstige vx(t)-grafiek.
5.2 Een steen wordt vanaf het dak van een hoog gebouw met een beginsnelheid van
29,4 m/s verticaal omhoog geworpen. Vier seconden later laat men vanuit hetzelfde
punt een andere steen vallen met beginsnelheid nul. Wanneer passeren de stenen
elkaar? En op welke diepte onder de dakrand?
5.3 Carl Lewis versnelt de eerste 4,0 seconden van de 100 m sprint tot zijn maximale
snelheid, die hij dan aanhoudt. Als hij de 100 m aflegt in 9,8 s, wat is dan zijn
gemiddelde versnelling gedurende de eerst 4,0 s?
5.4 Een auto wacht voor het rode licht. Nadat het licht groen wordt rijdt de auto
gedurende 6,0 s eenparig versneld ( a = 2,0 m/s2) en vervolgens voert hij een
eenparige beweging uit. Op het ogenblik dat de auto aan het rode licht vertrekt
passeert een vrachtwagen die in dezelfde zin rijdt met een constante snelheid van 10
m/s.
Wanneer en hoever voorbij het rode licht haalt de auto de vrachtwagen in?
Teken de x(t)-grafiek voor de auto én de vrachtwagen (dezelfde grafiek!)
5.5 Met welke snelheid moet een bal van een horizontaal tafelblad afrollen om in de
horizontale worp dezelfde horizontale als verticale verplaatsing te ondergaan bij het
neerkomen op de grond? De tafel is 95,2 cm hoog.
5.6 Men richt horizontaal met een geweer op een schietschijf op 150 m afstand. De
kogel komt 3,25 cm onder de roos terecht. Hoe groot was de beginsnelheid van de
kogel.
5.7 Een sportwagen haalt een snelheid van 240 km/h. De diameter van de wielen
bedraagt 56,2 cm. Bereken het toerental van de wielen.
5.8 Een massapunt beweegt op een rechte baan (x-as) met een versnelling waarvan
de getalcomponent is: ax = 2,5 t
Op het tijdstip to = 0,0 s bedraagt de snelheid 4,0 m/s.
Na 2,0 s bevindt het punt zich op de positie x = 6,0 m.
Evalueren in 5-de jaar fysica blz.9
Stel de snelheidsvergelijking en de bewegingsvergelijking op van dit bewegend
massapunt.
5.9 Een gocart rijdt de eerste helft van een 100 m rechte baan met een constante
snelheid van 5,0 m/s. Tijdens de tweede helft remt hij af met 0,20 m/s².
Gevraagd : Hoe lang duurt het om die 100 m af te leggen?
5.10 Een jachtbommenwerper vertrekt van op een vliegdekschip. Om niet in zee te
vallen moet hij na een afstand van 125 m een snelheid halen van 200 km/h. In de
veronderstelling dat zijn beweging een EVRB is, welke constante versnelling moet hij
daar dan voor hebben? Na hoeveel tijd bereikt hij 200 km/h?
5.11 Een formule-1-piloot stevent recht op een muur af. In een ultieme poging gaat
hij, als hij nog 50 m van de muur is, op zijn rem staan. Vanaf dat ogenblik is zijn
bewegingsvergelijking gegeven door: x(t) = - 15 m/s2 . t2 + 55 m/s . t met x in m.
Slaagt hij in zijn poging? Toon aan.
5.12 Een trein rijdt aan 108 km/h als de verstrooide machinist plots wakker schiet en
80 m voor zich een boemeltrein aan 54 km/h op hetzelfde spoor ziet uitrijden. Hoe
groot moet de constante vertraging minstens zijn waarmede de machinist moet
remmen om een botsing te vermijden. Hoe lang zal hij moeten afremmen?
5.13 Een voetbal wordt onder een hoek van 45,0° weggetrapt met een snelheid van
20,0 m/s naar een doelman de 60,0 m verder staat. Op hetzelfde ogenblik loopt de
doelman naar de bal toe.
• Stel voor de beweging van de bal de kinematische bewegingsvergelijkingen op.
• Leid hieruit de maximumhoogte en de dracht van de bal af.
• Met welke constante snelheid zal de doelman moeten lopen om
de bal te kunnen opvangen juist voor die de grond raakt?
6 Inzichtvragen
6.1 Een trein vertrekt uit het station. Jan zit stil in de rijdende trein. Is het station in
rust of in beweging t.o.v. Jan? Motiveer!
6.2 Welke baan en welk soort beweging maakt:
• een persoon die een wenteltrap bestijgt t.o.v. een persoon
die beneden de trap staat.
• een balletje dat in een rijdende trein verticaal wordt opgegooid ten opzicht van
een toeschouwer op het perron.
6.3 Bij een ECB blijft de grootte van de snelheid constant. Leg uit waarom de ECB
toch een versnelde beweging is. Maak de nodige figuren.
6.4 Is de vorm van de paraboolbaan bij een schuine worp afhankelijk van de massa
van het projectiel? Wat is hiervoor de fundamentele reden?
6.5 Een kogel hangt aan een touw dat een slingerbeweging maakt. Als de kogel in
zijn hoogste punt is wordt het touw doorgeknipt. Hoe beweegt de kogel:
Evalueren in 5-de jaar fysica blz.10
7 Doevraag
7.1 Van een wagentje dat uit rust vertrekt en dat door een massa aan een katrol
wordt voortgetrokken meet men op verschillende tijdstippen de positie. Onderzoek of
we hier te maken hebben met een EVRB.
Evalueren in 5-de jaar fysica blz.11
2 DYNAMICA
1 Meerkeuzevragen
1.1 Iemand duwt horizontaal tegen een kast van 36 kg. De persoon duwt met een
constante kracht van 40 N. De kast komt niet in beweging. De wrijvingskracht is dan
op dat ogenblik:
• 0,0 N
• 4,0 N
• 36 N
• 40 N
1.2 Met welke horizontale kracht moet je trekken aan een blok met massa 5,0 kg om
deze horizontaal te verplaatsen met een constante snelheid van 20,0 m/s. De
wrijvingsfactor is 0,200.
• 0,0 N
• 9,8 N
• 20 N
• 49 N
1.3 Het gewicht van een lichaam in rust in een stilstaande lift is:
• ... dat van hetzelfde lichaam in een lift die omhoog vertrekt
• ... dat van hetzelfde lichaam in een lift die eenparig stijgt
• ... dat van hetzelfde lichaam in een lift die dalend afremt
• ... dat van hetzelfde lichaam in een lift die stijgend afremt
Vul aan met <, > of =
1.4 Twee vrachtwagens A en B. De massa van vrachtwagen B is dubbel zo groot als
de massa van A. Vrachtwagen B rijdt met een snelheid die dubbel zo groot is als de
snelheid van A. Wat weet je over de kinetische energie van deze vrachtwagens?
• Ek, B = 2 x Ek,A
• Ek, B = 4 x Ek,A
• Ek, B = 6 x Ek,A
• Ek, B = 8 x Ek,A
• Ek, B = 16 x Ek,A
1.5 Een meisje van 56,0 kg in rust op een horizontaal vlak weegt aan de polen
• 550 N
• 549 N
• 548 N
• 547 N
1.6 Een balletje (1) wordt in een spiraalvormige buis geblazen (zie tekening in
bovenaanzicht). Welke weg zal het volgen uit de buis?
• (2)
• (3)
• (4)
• (5)
Evalueren in 5-de jaar fysica blz.12
2 Juist of fout
2.1 Een motorrijder helt in een bocht op een horizontaal wegdek over een hoek α
Zijn volgende uitspraken juist of fout:
• De hellingshoek α verdubbelt als de snelheid van de motorrijder verdubbelt.
• De hellingshoek α wordt groter als de massa van de motorrijder groter is.
• De hellingshoek α wordt groter als de fietser een scherpere bocht neemt.
2.2 Als twee satellieten met massa 120 kg en 560 kg op dezelfde hoogte draaien
boven het aardoppervlak, dan is hun snelheid even groot.
2.3 Twee loden bollen met respectievelijke massa van 1 kg en van 10 kg. Als je
beide bollen van op dezelfde hoogte loslaat, dan valt het lichaam van 10 kg sneller
naar beneden.
3 Reproductie
3.1 Een blokje met massa m (150 g) hangt in rust aan een veer.
Welke krachten werken in op het blokje: benoem, bereken de grootte en teken (met
lat).
Wat is het gewicht van het blokje? Leg uit.
Welke twee krachten zijn hier actie en reactie? Leg uit!
Evalueren in 5-de jaar fysica blz.13
3.2 Van welke factoren is de valversnelling op de aarde afhankelijk? Leid, waar
mogelijk een formule af die deze afhankelijkheid uitdrukt.
3.3 Satellieten kunnen in een parkeerbaan rond de aarde vliegen. Welke snelheid
moeten ze dan hebben?
4 Grafieken interpreteren / opstellen
4.1 Op een massa van 4,0 kg werkt een kracht in met constante richting en zin. De
Fx(t)- grafiek is hieronder getekend:
Fx (N)
4,0
3,0
2,0
1,0
0,0
0,0
2,0
4,0
6,0
8,0
t (s)
Bereken de krachtstoot in het tijdsinterval [0,0 ; 7,0] s.
Bereken de eindsnelheid van de massa die oorspronkelijk in rust was.
Hoe groot is de gemiddelde waarde van Fx in het tijdsinterval [0,0 ; 7,0] s.
4.2 Teken de grafiek die de grootte van de centripetale kracht weergeeft in functie
van de periode. Stel daartoe eerst een formule op die de centripetale kracht geeft in
functie van de periode.
4.3 Bereken de arbeid die de zwaartekracht levert op een voorwerp van 2,0 kg, dat in
het zwaarteveld de baan abc volgt. (Zie onderstaande figuur)
Evalueren in 5-de jaar fysica blz.14
4.4 Bij een proef met het wiel van Maxwell heeft men een aantal metingen en
berekeningen gedaan. Het vertrekpunt ligt 50 cm boven het laagste punt dat kan
bereikt worden. De energie van het wiel is 100 J in het vertrekpunt. Bij elke op- en
neergaande beweging gaat telkens ongeveer 20% van de overgebleven energie
verloren. Het aantal uitgevoerde bewegingen is naast de overgebleven energie
gegeven.
n: aantal uitgevoerde bewegingen
0
1
2
3
4
5
E(J)
100
80
64
51
41
33
Teken de E(n)-grafiek.
Bereken de hoogte (t.o.v. de laagste stand) die de massa nog bereikt na vier
bewegingen.
5 Rekenvragen
5.1 Een blok van 4,0 kg kan wrijvingsloos langs een helling verschuiven. De helling
maakt een hoek van 30° met het horizontale vlak. Het blok wordt geplaatst tegen een
veer met veerconstante 2000 N/m. Het blok wordt vervolgens tegen de veer gedrukt
tot de veer over een afstand van 0,20 m is ingedrukt. Vanuit deze positie wordt het
blok losgelaten.
Welke afstand zal het blok langs de helling afleggen?
5.2 De massa’s van A en B in de figuur zijn respectievelijk 150 g en 20,0 g. Het
wagentje komt, door de aantrekkingskracht van de aarde op de aandrijfmassa B in
Evalueren in 5-de jaar fysica blz.15
beweging. De wrijving van het wagentje met de tafel en het touw met de katrol is
verwaarloosbaar.
Bereken de aandrijfkracht.
Welke massa moet C hebben opdat de versnelling van het wagentje 0,800 m/s2 zou
bedragen?
5.3 Een massa van 25,3 kg beweegt eenparig rechtlijnig met een snelheid van 20,0
km/h. Hoe groot is de nettokracht?
Een massa van 25,3 kg beweegt eenparig cirkelvormig (r = 70,3 m) en met een
snelheid van 20 km/h. Hoe groot is de nettokracht?
5.4 Bereken de gravitatiekracht op aarde op een persoon met een massa van 70,5
kg.
5.5 Een doos van 30,0 kg, oorspronkelijk in rust, wordt door een kracht van 90,0 N
onder een hoek van 44° met de horizontale over een afstand van 10,0 m over een
horizontale vloer voortgetrokken.
De wrijvingsfactor is 0,0300.
Bereken de arbeid geleverd door de uitgeoefende kracht.
Bereken de arbeid geleverd door de wrijvingskracht.
Bereken de eindsnelheid van de doos.
5.6 Bereken de arbeid als Fx = 3x2 - 5,0 met [Fx] = N en het voorwerp beweegt van x1
= 4,0 m tot x2 = 7,0 m.
5.7 Een bol met massa 4,0 kg en een snelheid van 2,4 m/s botst centraal met een
stilliggende bol met massa 8,0 kg. Bereken de snelheden van beide bollen na de
volkomen elastische botsing. Bereken de impulsverandering van elk van de bollen.
5.8 Een auto heeft een massa van 1,3 ton. In 9,8 s voert de motor de snelheid van
de wagen op van 79,6 km/h tot 126 km/h. Hoe groot is het vermogen dat de motor
moet ontwikkelen?
Hoe groot zal de remafstand zijn bij de grootste snelheid?
5.9 Een massa m1 = 0,590 kg botst elastisch met een snelheid van 0,75 m/s tegen
een massa m2 = 0,350 kg in rust op een wrijvingsloos oppervlak.
Bereken de snelheid en de bewegingszin van elke massa na de botsing.
Evalueren in 5-de jaar fysica blz.16
De massa m2 botst elastisch tegen een volkomen elastische wand (verwaarloosbare
botsingstijd) en botst nadien opnieuw tegen massa m1. Waar grijpt de tweede botsing
plaats? (Plaats van het punt a). De massa’s worden als punten beschouwd.
5.10 Een lichaam met massa 3,00 kg beweegt eenparig op een horizontaal
oppervlak met snelheid v0. Een kracht van 18,0 N werkt in tegengestelde zin aan de
beweging en herleidt de snelheid tot v0/2 terwijl het lichaam 9,00 m aflegt. Hoelang
duurde die vertraging?
5.11 Een persoon van 70 kg laat zich langs een verticaal touw van 6,0 m met een
EVRB naar beneden glijden. Hij landt op de grond met een snelheid van 21,6 km/h.
Hoeveel remkracht oefent hij uit op het touw?
6 Inzichtvragen
6.1 Zowel aan de evenaar als aan de polen plaatst men op een stilstaande
weegschaal een hoeveelheid suiker zodat het gewicht ervan telkens 10 N is.
Krijgt men in beide gevallen evenveel suiker? Zo neen, waar heeft men het meest
suiker? Verklaar!
6.2 Aristoteles dacht dat een constante kracht aan een lichaam een constante
snelheid gaf. Daaruit besloot hij dat, als de kracht ophoudt met inwerken, het lichaam
tot rust komt.
Wat vertelt Newton hierover? Geeft hij Aristoteles gelijk? Leg uit!
6.3 Verklaar aan de hand van de beginselen van Newton:
• Met een korte ruk, kun je blaadje per blaadje van een rol toiletpapier trekken. Trek
je gelijkmatig dan rolt het papier af.
• Een jager houdt het geweer tegen zijn schouder als hij een kogel afvuurt.
• Als een auto bruusk stopt, hebben de inzittenden de neiging om ten opzichte van
hun zetel naar voor te bewegen.
• Maakt een wagen een scherpe bocht, dan zijn de inzittenden geneigd naar de
buitenkant van de bocht te schuiven.
• Een vrachtwagen geladen met boomstammen moet plots heel hevig remmen. De
chauffeur raakt bij dit manoeuvre geklemd in zijn cabine.
6.4 Schrap wat niet past en verklaar.
Evalueren in 5-de jaar fysica blz.17
Als een vallend voorwerp de grond raakt dan is op dat ogenblik de kracht die wordt
uitgeoefend door de vaste grond op het voorwerp (groter / even groot / kleiner) dan
het gewicht van dat lichaam.
6.5 Twee personen staan op rolschaatsen en duwen tegen elkaar. De wrijving mag
worden verwaarloosd. Bespreek (volledig) wat er gebeurt.
6.6 Neem deze figuur over op je antwoordblad.
Een persoon met massa 65,0 kg staat in een lift in rust.
• Bereken en teken de zwaartekracht die inwerkt op de persoon.
• Bereken en teken het gewicht van de persoon t.o.v. de lift.
• De lift stijgt met een constante snelheid van 0,50 m/s. Hoe groot is het gewicht
nu?
• De lift heeft bijna het gelijkvloers bereikt, komende van de tweede verdieping. Hij
vertraagt met 2,00 m/s2. Bereken opnieuw het gewicht.
6.7 Laura staat op rolschaatsen en duwt tegen een muur. Wat gebeurt er? Waarop
steunt deze waarneming? Verklaar aan de hand van een schets.
6.8 Wanneer iemand een zware kast wil verschuiven maar de kast blijft staan en de
persoon zelf glijdt achteruit: gaat de wet actie en reactie dan nog op?
6.9 Leg uit wat er gebeurt met de vracht in de laadbak van een vrachtwagen als de
bestuurder bruusk moet remmen?
6.10 Er wordt tegen een voorwerp geduwd. De wrijvingskracht werkt in tegengestelde
zin en het voorwerp verplaatst zich niet. Toch zijn die duwkracht en de wrijving niet
elkaars actie- en reactiekrachten. Waarom niet?
6.11 Hoe groot wordt de gravitatiekracht op een persoon als de straal van de aarde
zou verdubbelen, terwijl de massa van de aarde constant blijft?
6.12 Hoe groot wordt de gravitatiekracht op een persoon als de straal van de aarde
zou verdubbelen, terwijl de massadichtheid van de aarde constant blijft?
7 Doevragen
7.1 Je staat op een personenbalans en je noteert je massa. Je buigt eerst snel en
daarna traag door je knieën en je beschrijft en verklaart wat er gebeurt. Daarna sta je
met gebogen knieën op de balans en je komt eerst vlug en daarna traag weer in
gestrekte toestand. Verklaar wat er gebeurt.
Evalueren in 5-de jaar fysica blz.18
Evalueren in 5-de jaar fysica blz.19
3 EVENWICHT
1 Meerkeuzevraag
1.1 Op twee balansen A en C rust een lat. Op het punt B is een massa geplaatst. De
afstand tussen de punten A en B is één vierde van de totale lengte van de lat. De
massa van de lat zelf mag worden verwaarloosd. Op balans A lezen we af: 12 kg.
Dan is de aanduiding op de balans C:
•
•
•
•
36 kg
3,0 kg
4,0 kg
48 kg
2 Juist of fout vraag
2.1 Een lichaam dat in evenwicht is, is altijd in rust.
2.2 De stabiliteit van een bloempot vermindert wanneer de plant hoger opschiet.
3 Reproductievragen
3.1 Aan welke voorwaarden moeten voldaan zijn opdat een lichaam in evenwicht zou
zijn?
4 Grafieken interpreteren / opstellen
5 Rekenvraag
5.1 Een plank met lengte 2,00 m en massa 10,0 kg wordt gebruikt als brug over een
beek. Een kind met massa 35 kg staat op de plank.
De rechterkant van de plank oefent op de oever een kracht uit die tweemaal zo groot
is als de kracht die de linkerkant uitoefent. Maak een tekening van deze situatie. Op
welke afstand van de rechterkant staat het kind? Hoe groot zijn de krachten die de
brug uitoefent op de rechter- en linkeroever?
Evalueren in 5-de jaar fysica blz.20
5.2 Een homogene bol met massa 5,00kg hangt in rust tegen een verticale muur. Het
touw maakt met de muur een hoek van 30°.
A) Teken en benoem alle krachten die op de bol inwerken.
B) Bereken de grootte van elk van deze krachten.
5.3 Een homogene balk met rustgewicht 2000 N en lengte 3,00 m is aan zijn linker
uiteinde via een scharnier vastgemaakt aan een rechtopstaande muur. Een kabel,
vastgemaakt aan de muur op een afstand van 1,80 m boven het scharnier, is
verbonden met het rechter uiteinde van de balk. Aldus maakt de balk een hoek van
30,0° met de horizontale. Tenslotte wordt in het rechter uiteinde van de balk een
betonnen blok van 1500 N via een touw opgehangen. Bereken de grootte van de
spankracht in de kabel.
5.4 Een balk doet dienst als stelling, het linker uiteinde wordt ondersteund door een
muurtje en het rechter uiteinde hangt aan vast aan een ketting. De afstand tussen
het steun- en ophangpunt is 2,00 m lang. De balk heeft een massa van 40 kg. Op
0,50 m van het linker uiteinde staat een persoon van 60 kg.
Teken op de figuur de krachten die inwerken op de balk.
Bereken de spankracht in de ketting.
5.5 Een kruiwagen heeft een gewicht van 180 N. Het zwaartepunt van de kruiwagen
ligt op 0,40 m van de as van het wiel. De afstand van de as van het wiel tot de
handvaten is 1,80 m. De kruiwagen wordt gevuld met zand. Men zorgt bij het vullen
van de kruiwagen dat het zwaartepunt van het zand op 0,60 m van de as van het
wiel ligt.
Maak een duidelijke schets en duidt er alle krachten en afstanden op aan.
Bereken de massa zand die op de kruiwagen geplaatst mag worden om hem met
een kracht van 200 N op te tillen. Ook deze kracht van 200 N stel je op de
bovenstaande tekening voor.
Welke kracht oefent het wiel uit op de grond bij het optillen van de kruiwagen?
6 Inzichtvraag
6.1 Een valschermspringer van 90 kg daalt met een snelheid van 15 km/h. Hoe groot
is de wrijvingskracht die de lucht uitoefent op de persoon en het valscherm?
Waarom?
Evalueren in 5-de jaar fysica blz.21
7 Doevraag
7.1 Aan een koord hangt een massa. Construeer de spankrachten in de koord.
Welke eenvoudige proef moet je uitvoeren om te weten of er werkelijk spankrachten
werken?
Evalueren in 5-de jaar fysica blz.22
4 ELEKTROSTATICA EN CONDENSATOREN
1 Meerkeuze
1.1 Twee identieke metalen bollen A en B dragen respectievelijke ladingen - Q en +
2Q.
De afstand tussen de middelpunten van de bollen is d.
De grootte van de elektrostatische kracht is F.
Indien men de afstand halveert, wordt de grootte van deze kracht:
F
•
4
F
•
2
• 2F
• 4F
1.2 Welke figuur geeft de juiste voorstelling van de ladingverdeling die optreedt,
wanneer we een negatief geladen voorwerp A in de buurt brengen van een
ongeladen elektroscoop, zonder de elektroscoop aan te raken.
1.3 In welke van de gebieden A, B, C kan een kleine positieve lading in rust zijn en
blijven? Verklaar!
1.4 Vier puntladingen +Q, -Q, +Q en -Q zitten op de hoekpunten van een vierkant
met zijde r. Men laat de ladingen vrij. Hoe gaan ze bewegen:
Evalueren in 5-de jaar fysica blz.23
•
•
•
•
Naar het middelpunt toe (volgens de diagonalen)
Van het middelpunt weg (volgens de diagonalen)
Ze beschrijven een cirkel met als middelpunt het snijpunt van de diagonalen
Ze bewegen niet en blijven op hun zelfde plaats
1.5 Je hebt twee ladingen Q1 en Q2. Beide zijn in vacuüm geplaatst op een afstand r.
De kracht tussen beide wordt voorgesteld door F
Q1
A
Dan geldt:
• voor punt B dat
• voor punt B dat
• voor punt B dat
• voor punt B dat
EB =
EB =
EB =
EB =
r
Q2
B
F /Q2
F /Q1
F .Q1
F .Q2
1.6 We plaatsen drie van de grond geïsoleerde geleiders in elkaar nabijheid zoals op
de figuur. Geleider A wordt negatief geladen. Dan geldt:
• geleider B wordt positief geladen.
• de linkerkant van B wordt negatief geladen.
• geleider C blijft neutraal.
• we kunnen geen uitspraak doen over geleiders B en C.
Verklaar uw antwoord m.b.v. schetsen.
A
B
C
2 Juist of fout
2.1 In een elektrisch veld beweegt een proeflading onder invloed van de
coulombkracht steeds van hoge naar lage potentiaal.
Evalueren in 5-de jaar fysica blz.24
2.2 Een geladen bolvormige geleider (straal R) bevat een lading -Q. (zie figuur)
•
•
•
Als Q’ naar Q toe verplaatst wordt vergt dit negatieve / positieve arbeid. Verklaar.
De veldsterkte heeft in b dezelfde / tegengestelde zin als de coulombkracht die de
lading Q’ in dat punt ondervindt. Verklaar.
De punten a en d liggen op hetzelfde / een verschillend equipotentiaal oppervlak.
Verklaar.
2.3 Papiersnippers kan je aantrekken met een plastic pen, gewreven met een wollen
doek.
2.4 In een punt A midden tussen twee even grote maar tegengestelde puntladingen
Q1 en Q2 plaatst men een negatieve puntlading Q3.
Q1
-
.
A
Q2
+
Beoordeel volgende uitspraken:
• De resulterende kracht op Q3 vanwege Q1 en Q2 wijst naar rechts.
• Op Q3 werkt geen resulterende kracht in.
• De resulterende veldsterkte in A vanwege Q1 en Q2 is nul.
• De resulterende veldsterkte in A wijst naar rechts.
• Als Q1 en Q2 verdubbelen, dan verdubbelt ook de resulterende kracht op Q3.
2.5 De potentiaal buiten het veld is nul. Als je bij het radiaal veld van een negatieve
bronlading staat dan is de potentiële elektrische energie van een positieve lading
altijd negatief.
2.6 Een gewreven plastic staaf kan een waterstraal scheeftrekken.
3 Reproductie
3.1 Beantwoord volgende vragen met formules:
Evalueren in 5-de jaar fysica blz.25
• Welke arbeid levert het veld om de lading Q1 van b naar c te brengen?
• Hoe berekent men de potentiële energie van Q1 in b?
• Hoe verandert de potentiële energie van Q1 als ze van b naar a gebracht wordt?
• Hoe berekent men de potentiaal in c?
• Hoe berekent men de veldsterkte in d?
Stel grafisch de potentiaal voor als functie van de afstand tot het midden van de bol.
3.2 Nader je de knop van een negatief geladen elektroscoop met een flink gewreven
glasstaaf, dan zie je de uitwijking van de naald eerst kleiner worden, vervolgens nul
worden en daarna weer toenemen. Verklaar dit en illustreer met een tekening.
3.3 Een elektroscoop (A) wordt door contact positief geladen. Verklaar het optreden
van de uitwijking.
• De positief geladen elektroscoop (A) wordt in de buurt gebracht (geen contact)
met een andere positief geladen elektroscoop (B). Wat zal er gebeuren met de
uitwijking van elektroscoop (A)? Verklaar met een tekening.
• De positief geladen elektroscoop (A) wordt nu in contact gebracht met een
andere positief geladen elektroscoop (B). Is het mogelijk dat hierdoor de
uitwijking van elektroscoop (A) vermindert? Verklaar met een tekening.
3.4 Welke factoren hebben invloed op de capaciteit van een vlakke condensator.
Bespreek kort en verklaar met een experiment.
3.5 We naderen een neutrale elektroscoop met een negatief geladen staaf.
- Wijkt de elektroscoop uit? Waarom wel? Waarom niet?
- Krijgt de elektroscoop een lading?
- Maak een tekening en verklaar aan de hand van de atoomstructuur.
- Hoe noemt men dit verschijnsel?
- Wat zien we als we de elektroscoop aarden terwijl we de staaf in de buurt houden?
- Maak een tekening en verklaar aan de hand van de atoomstructuur.
3.6 Hoe kan men door inductie een elektroscoop negatief opladen?
4 Grafieken interpreteren / opstellen
4.1 Een bolvormige geleider met straal 5,0 cm draagt een positieve lading. Schets de
grafiek van de potentiaal V in functie van de afstand r tot het middelpunt van de bol.
4.2 Een bolvormige geleider heeft een diameter van 2,50 cm en draagt een lading
van –15,0 mC.
Bereken de veldsterkte op 3,00 cm en 4,00 cm van het middelpunt van de bol.
Teken de grafiek van de veldsterkte E in functie van de afstand r tot het middelpunt
van de bol.
5 Rekenvragen
5.1 Als er geen resulterende kracht inwerkt op Q3, bereken dan hoe groot Q1 is als
Q2 = 1,00 nC.
Evalueren in 5-de jaar fysica blz.26
5.2 Een deeltje met lading Q = +7,3.10-6 C bevindt zich in een homogeen elektrisch
veld met veldsterkte E = 150 N/C op 4,0 cm van de negatieve plaat. Bereken de
potentiële energie van de lading Q.
5.3 Beschouw drie puntladingen, gelegen op de hoekpunten van een driehoek
(figuur).
Q1 = Q3 = 5,00 µC en Q2 = -2,00 µC; a = 0,100 m. Bepaal de resulterende kracht op
de lading Q3.
Bereken de afzonderlijk krachten; stel ze vectorieel voor en teken en bereken de
resulterende kracht.
5.4 Bereken de substitutiecapaciteit tussen de punten A en B: C1 = 24 pF; C2 = 12
pF; C3 = 12 pF; C4 = 6,0 pF en C5 = 6,0 pF
5.5 Twee bolletjes hebben elk een massa van 90,0 g en dragen beiden een
elektrische lading +1,00 µC. Ze zijn met twee even lange draadjes in één punt
opgehangen. Ze stoten elkaar af en bevinden zich op 12,0 cm van elkaar. Bereken
de lengte van de touwtjes.
5.6 In elk hoekpunt van driehoek abc bevindt zich een lading. In a en c is dit een
lading van – 6,0 µC. In b is dit 10,0 µC.
a) Bereken de elektrische veldsterkte in p.
b) Bereken de potentiaal in p.
Evalueren in 5-de jaar fysica blz.27
5.7 Op de hoekpunten van een vierkant met zijde 30 cm bevinden zich 3 identieke
ladingen van 5,0 µC. Teken en bereken de veldsterkte in het vierde hoekpunt.
Bereken de arbeid om een lading van –3,0 µC te verplaatsen van het vierde
hoekpunt naar het middelpunt.
6 Inzichtvragen
6.1 Een neutrale metalen staaf S is geïsoleerd opgesteld. Tegen het rechtse uiteinde
hangt men een metalen bolletje. Wat gebeurt er met het bolletje als we een positieve
staaf vlak bij het linkse uiteinde van de staaf houden (zonder de staaf aan te raken).
Verklaar!
6.2 Een klein neutraal geleidend bolletje is opgehangen aan
een niet-geleidend touwtje. Het hangt in de buurt van een
positief geladen bol, die geïsoleerd staat van de aarde.
Verklaar waarom het geleidend bolletje eerst wordt aangetrokken.
Nadat het contact gemaakt heeft met de positief geladen bol wordt het bolletje
afgestoten. Waarom?
Zou het voorgaande ook lukken als de grote bol geaard is? Waarom? Waarom niet?
6.3 Vergelijk een radiaal veld met een homogeen veld wat betreft veldlijnen,
veldsterkte en potentiaal.
6.4 Op de X-as bevinden zich twee puntladingen die in rust zijn. De eerste puntlading
is gelijk aan + 4 Q en bevindt zich in x = 0 cm.
De tweede puntlading is gelijk aan + Q en bevindt zich in het punt x = 6 cm.
Op welke plaats op de X-as (x = ?) bevindt zich het punt waar de elektrische
veldsterkte gelijk aan nul is?
(De waarde van Q heb je niet nodig om dit vraagstuk op te lossen, maar je kan
desnoods zelf een willekeurige waarde voor Q kiezen.)
Evalueren in 5-de jaar fysica blz.28
6.5 Twee puntladingen Q1 en Q2 oefenen bij een onderlinge afstand van 0,60 m een
afstotende kracht van 2,0 N op elkaar uit. Vervangt men lading Q2 door een positieve
puntlading Q3, dan blijkt dat deze op lading Q1 een aantrekkende kracht van 6,0 N
uitoefent. Wat volgt hieruit voor de aard van de puntladingen Q1 en Q2 en wat is de
verhouding tussen de ladingen Q2 en Q3?
6.6 Een positief opgeladen elektroscoop wordt in contact gebracht met een andere
positieve lading. Kan de uitwijking verminderen?
6.7 Door elektrostatische inductie kunnen we een elektroscoop blijvend positief
laden. Leg uit hoe dit gebeurt.
7.Doevragen
7.1 Je wrijft een glazen staaf op met een kattenvel. De glazen staaf is draaibaar
opgesteld. Wat gebeurt er als je het gewreven deel van het kattenvel nadert naar het
gewreven deel van de staaf? Wat kan je uit deze proef besluiten? Verklaar!
Evalueren in 5-de jaar fysica blz.29
5 ELEKTRISCHE STROOM IN GELEIDERS
1 Meerkeuze
1.1 We willen de stroomsterkte door een weerstand en de spanning over die
weerstand meten met een ampèremeter en een voltmeter.
De nauwkeurigste resultaten worden bekomen met de voltmeter en de ampèremeter
waarvan de inwendige weerstand:
• RA = 50 Ω en RV = 50 Ω
• RA = 5 Ω en RV = 500 Ω
• RA = 500 Ω en RV = 500 Ω
• RA = 50 Ω en RV = 500 Ω
1.2 De weerstand van een draadgeleider zal verdubbelen als men:
• De lengte van de draad ongewijzigd laat en de diameter verdubbelt
• De draad 4 x langer maakt en de diameter verdubbelt
• De draad 2 x langer maakt en de diameter op de helft van de oorspronkelijke
waarde brengt
• De draad 8 x langer maakt en de diameter verdubbelt
• De lengte van de draad ongewijzigd laat en de diameter op de helft van de
oorspronkelijke waarde brengt.
1.3 Bij het sluiten van schakelaar S zal de stroom door de bron geleverd:
•
•
•
•
onveranderd blijven
verdubbelen
stijgen met 0,5 A
dalen met 0,5 A
1.4 De weerstand van een draad is 9,0 Ω De doorsnede van de draad 2,0 mm². Als
je de doorsnede van de draad op 3,0 mm² brengt dan wordt de waarde van de
weerstand:
• 4,0 Ω
• 6,0 Ω
• 13,5 Ω
• 20,25 Ω
Evalueren in 5-de jaar fysica blz.30
1.5 De stroomsterkte in een strijkijzer met weerstand 55 Ω indien het op een
spanning van 230 V wordt geschakeld is:
• 0,24 A
• 4,2 A
• 4,2.10³ A
• 0,42 A
1.6 De resistiviteit van metalen:
• is even groot als de resistiviteit van de niet metalen
• is kleiner dan de resistiviteit van de niet metalen
• is groter dan de resistiviteit van de niet metalen
1.7 Men rekt een geleidende draad zodanig uit dat zijn lengte precies verdubbelt. In
de veronderstelling, dat volume van de draad hierbij niet verandert, kunnen we hieruit
afleiden dat:
• de weerstand tweemaal zo groot wordt;
• de weerstand viermaal zo groot wordt;
• de weerstand gelijk blijft;
• de weerstand tweemaal zo klein wordt.
1.8 Van 4 draden A, B, C en D zijn volgende gegevens gekend:
Draad
A
B
C
D
Lengte
L
2L
L
2L
Doorsnede
A
A
2A
2A
Resistiviteit
ρ
2ρ
ρ
2ρ
De draad (draden) met de grootste elektrische weerstand is (zijn) dan:
• A
• B
• C
• A en D
1.9 In het achterlichtje van een fiets zit een lampje waarop staat: 6 V en 0,05 A. Hoe
groot is de weerstand van dit achterlichtje?
•
•
•
•
0,0080 Ω
0,30 Ω
6,0 Ω
120 Ω
1.13 De vervangingsweerstand tussen de punten A en B is:
Evalueren in 5-de jaar fysica blz.31
•
•
•
•
2R
3R
2/3 R
0
2 Juist of fout
2.1 Een koperen draad heeft een weerstand R, een koperen draad met dezelfde
R
lengte maar met een doorsnede die 4 keer groter is, heeft dan een weerstand .
4
2.2 Als meer weerstanden in serie geschakeld worden, dan wordt de totale
weerstand groter.
2.3 Als meer weerstanden in parallel geschakeld worden, dan wordt de totale
weerstand groter.
2.4 In onderstaande figuur zijn A, B, C, D en E identieke lampjes. In de schakeling
mogen de weerstanden van de verbindingssnoeren verwaarloosd worden. Beoordeel
elk van de volgende uitspraken.
•
•
•
•
Als lamp D niet brandt (losgedraaid), dan branden alle andere lampen even fel.
Alle lampen branden even fel
Als alle lampen branden, brandt D minder fel dan E
Als B en C niet branden (losgedraaid) dan brandt A feller dan D en E
2.5 Je beschikt over een spanningsbron (6,0 V) en twee weerstanden R1 = 20 Ω en
R2 = 40 Ω.
1 Teken de stroomkring waarin je de weerstanden in serie schakelt.
Evalueren in 5-de jaar fysica blz.32
•
•
De stroomsterkte is in beide weerstanden even groot.
De spanning over elke weerstand is even groot.
2 Teken de stroomkring waarin je de weerstanden in parallel schakelt.
• De stroomsterkte is in beide weerstanden even groot.
• De spanning over elke weerstand is even groot.
2.6 Uit de wet van Ohm volgt dat de weerstand van een geleider recht evenredig is
met de spanning die men erover legt.
2.7 Een spanningsbron produceert elektronen.
2.8 Bij een kortsluiting wordt de spanning erg groot.
3 Reproductie
3.1 Teken een stroomkring met een spanningsbron en een veranderlijke weerstand.
3.2 Leg het verschil uit tussen de bronspanning en de klemspanning.
3.3 Wat is de betekenis van de inwendige weerstand van de bron?
3.4 Toon aan dat een ampèremeter een kleine inwendige weerstand moet hebben
om betrouwbare meetresultaten op te leveren.
3.5 Brug van Wheatstone:
Maak een tekening.
Leid het verband af tussen de weerstanden als de brug in evenwicht is en formuleer
dit in woorden.
3.6 Maak een schema van de opstelling van de gebruikte stroomkring bij het
experimenteel afleiden van de formule voor de wetten van Pouillet. Benoem alle
onderdelen. Geef deze wet in formulevorm.
3.7 In vele stopcontacten zit een “aarding”. Waarom?
3.8 Welke energieovergangen kan je noteren bij de elektriciteitsproductie in een
klassieke thermische centrale.
3.9 Leid de formule af voor de vervangingsweerstand bij een parallelschakeling van
twee weerstanden.
4 Grafieken interpreteren / opstellen
4.1 Men schakelt een batterij in een kring met een vaste weerstand R0 en een
schuifweerstand R.
Evalueren in 5-de jaar fysica blz.33
Over de schuifweerstand R plaatst men een voltmeter.
Men doet een aantal metingen waarbij men bij geleidelijk stijgende waarden van R
de overeenkomstige aflezing U van de voltmeter noteert.
Welke van de onderstaande grafieken is de beste weergave van de meetresultaten?
4.2 Schets de grafiek die het verloop van de stroomsterkte weergeeft in functie van
de resistiviteit. (alle andere grootheden blijven constant). Hint: maak van twee
formules één.
4.3 Schets het verband tussen het elektrisch vermogen in functie van de
stroomsterkte voor een gegeven (= constante) weerstand.
4.4 Deze grafiek geeft het verband weer tussen de stroomsterkte door een
geleidende draad en de spanning over die draad.
• Hoe groot is de weerstand van die draad?
• Hoeveel stroom loopt er door de draad als de spanning 25 V bedraagt?
Evalueren in 5-de jaar fysica blz.34
5 Rekenvragen
5.1 Als door de doorsnede van een koperdraad onder netspanning (235 V) een
hoeveelheid lading van 253 C loopt in 12 s, wat is dan de weerstand van die draad?
5.2 Bereken de weerstand van drie toestellen met dezelfde weerstand, die
geschakeld zijn zoals hieronder is weergegeven. De stroom door de bron geleverd is
20 mA en zij levert 40 V spanning.
5.3 Op een lampje staat vermeld 12 V / 14 W. Men sluit het lampje aan op een
spanning van 10 V. Bereken de stroom door het lampje.
5.4 Men schakelt twee weerstanden respectievelijk 60,0 Ω en 90,0 Ω parallel en
verbindt in serie daarmee een weerstand van 24,0 Ω Het geheel is aangesloten op
een batterij met spanning 24,0 V.
• Teken de volledige stroomkring.
• Bereken de vervangingsweerstand.
• Bereken de stroomsterkte die de batterij levert.
• Bereken de spanning over elke weerstand.
• Bereken de stroomsterkte in de 60,0 Ω weerstand.
5.5 Op een toaster staan de volgende aanduidingen: 1400 W en 220 V. Wat
betekenen deze aanduidingen?
Hoeveel kost het om 30 toastjes te maken als elke toast 30 s in de broodrooster
steekt (prijs kWh = 6 BEF)
5.6 Op een toestel vinden we 1200 W. Door het toestel gaat 4,06 A. Op welke
spanning moet men dit toestel aansluiten? Bereken de weerstand van het toestel.
Hoeveel kost het elektrisch verbruik per uur als 1 kWh 5,70 BEF kost.
5.7 De verlichting van een fiets wordt gevoed door een dynamo die 6,0 V levert.
Indien de weerstand van het voorlicht 12 Ω bedraagt en de stroom door het
achterlicht 0,045 A, bereken dan de stroom door het voorlicht en de weerstand van
het achterlicht.
5.8 Twee lampen zijn voorzien om te functioneren in serie op 250 V. Dan is het
vermogen van de ene 25 W, dat van de andere 100 W.
Evalueren in 5-de jaar fysica blz.35
De twee lampen worden nu opgenomen in een andere schakeling. Om als voorheen
te branden (25 W, 100 W) moet voor elke lamp een gepaste weerstand in serie
geplaatst worden. Bepaal de waarden R1 en R2.
5.9 Bereken bij onderstaande schakeling de vervangingsweerstand.
Welke stroomsterkte levert de bron.
Welke spanning staat er over R1?
Welke spanning staat er over R2?
Welke stroomsterkte loopt er door R3?
Welke spanning staat er over R5?
5.10 Op een strijkijzer staan de aanduidingen: 230 V / 1500 W. Hoeveel moet je
betalen als je er 20 min op vol vermogen mee werkt en als 1 kWh 6,4 BEF kost.
Evalueren in 5-de jaar fysica blz.36
6 Inzichtvragen
6.1 Jan gaat in een huisje en in een station langs zijn spoorwegbaan verlichting
aanbrengen. Hij wil in het huisje één lampje en in het station twee lampjes
aansluiten. De 3 lampjes zijn identiek. Welke schakeling moet hij kiezen opdat de 3
lampjes even sterk zouden branden en met het grootste vermogen?
Verklaar!
6.2 Wat gebeurt er met de andere lampen (geven ze minder, meer, even veel of
helemaal geen licht meer) als er één lamp kapot gaat:
1 bij een serieschakeling van 5 lampen
2 bij een parallelschakeling van 5 lampen
Verklaar!
6.3 Teken de snoeren zodat het lampje brandt en je de stroomsterkte door het
lampje kan meten.
6.4 Een spanningsbron en vijf identieke lampjes zijn geschakeld volgens
onderstaand schema. Alle lampjes branden. Rangschik de lampjes in dalende
volgorde waarin ze licht geven.
Evalueren in 5-de jaar fysica blz.37
6.5 Indien de schakelaar s in onderstaand schakeling gesloten is, dan geeft de
voltmeter een spanning U1 aan.
Zal de spanning afgelezen op de voltmeter wijzigen als men de schakelaar s opent?
Verklaar.
6.6 Om de weerstand Rx te meten heeft men de brug "in evenwicht" gebracht. Wat
gebeurt er dan als men de weerstanden R1 en R2 van plaats verwisselt? Waarom?
6.7 Een weerstand is verbonden met een batterij. Wat gebeurt er met de
stroomsterkte als je in deze schakeling de spanning drie maal groter maakt en de
weerstand 2 maal kleiner?
Evalueren in 5-de jaar fysica blz.38
6.8 Een lamp voor de huisverlichting heeft een vermogen van 100 W bij 220 V. De
lamp van een overheadprojector heeft een vermogen van 250 W bij 24 V.
Welke lamp heeft de grootste weerstand?
Welke gloeidraad is het dikst als de lengte en het materiaal ervan hetzelfde zijn?
6.9 Je verbindt de polen van een spanningsbron door geleidende toevoerdraden met
een lampje. Teken deze schakeling.
Met welk meetinstrument meet je de stroom door het lampje?
Waar plaats je dit instrument in de schakeling? Zet dit op de vorige tekening. Met
welke meetinstrument meet je de spanning over het lampje? Waar plaats je dit
instrument in de schakeling? Zet dit ook op de vorige tekening.
6.10 We verbinden de uiteinden van een constantaandraad met de polen van een
spanningsbron. Voor verschillende waarden van een spanning wordt telkens de
stroomsterkte in de draad gemeten, dit levert ons volgende meetresultaten:
Spanning (V)
1,0
2,0
3,0
4,0
5,0
Stroomsterkte (A)
0,055
0,115
0,177
0,230
0,280
U/I
Welk verband bestaat ertussen de spanning en de stroomsterkte? (in woorden) De
verhouding... is bijgevolg constant.
Toon aan door deze verhouding te berekenen in de tabel.
Hoe noemt men deze verhouding: de naam
Geef ook het symbool en de eenheid van deze grootheid.
6.11 Bij een kerstboomverlichting kunnen de lampjes in serie of in parallel
geschakeld zijn. Hoe kan je zonder gebruik te maken van meetapparatuur nagaan
hoe ze geschakeld zijn?
6.12 Men kan op een huisinstallatie geen onbeperkt aantal elektrische toestellen
aansluiten. Waarom niet?
6.13 Op het lampje van het achterlicht van een fiets staat: 6,0 V; 0,050 A.
Op het lampje van het voorlicht van de fiets staat: 6,0 V; 0,50 A.
(Deze waarden slaan op maxima d.w.z. dat de spanning en de bijhorende
stroomsterkte deze waarden niet mogen overschrijden)
Iemand knutselt met deze lampjes de verlichting van zijn fiets zodanig dat beide
lampjes in serie in een kring staan met een spanningsbron, de dynamo, van 6,0 V.
Maak een schets.
Bereken de weerstand van de lampjes.
Welke bewering is juist:
• Beide lampjes branden even sterk.
• Het lampje van het achterlicht brandt niet.
• Het lampje van het voorlicht brandt niet.
• Beide lampjes branden niet.
Evalueren in 5-de jaar fysica blz.39
Verklaar uw keuze!
7.Doevragen