G36
Kommagetallen vermenigvuldigen en delen
Op verkenning
a
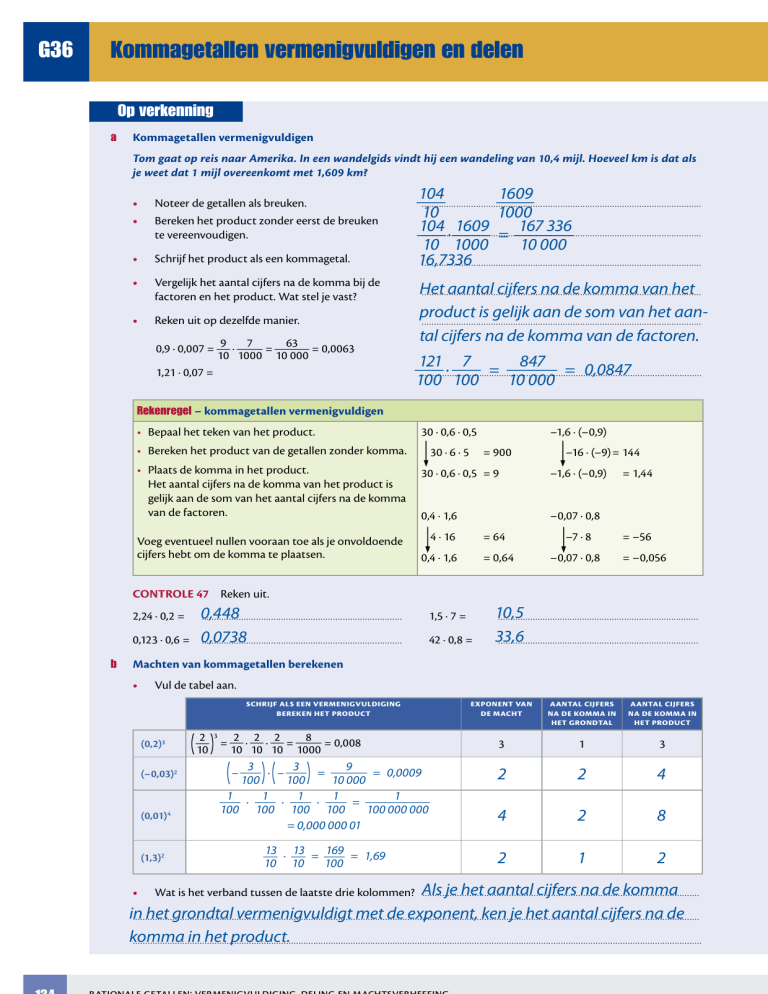
Kommagetallen vermenigvuldigen
Tom gaat op reis naar Amerika. In een wandelgids vindt hij een wandeling van 10,4 mijl. Hoeveel km is dat als
je weet dat 1 mijl overeenkomt met 1,609 km?
t
t
Noteer de getallen als breuken.
Bereken het product zonder eerst de breuken
te vereenvoudigen.
t
Schrijf het product als een kommagetal.
t
Vergelijk het aantal cijfers na de komma bij de
factoren en het product. Wat stel je vast?
t
Reken uit op dezelfde manier.
9 _
63
7 0,9 · 0,007 = _ · = _ = 0,0063
10 1000 10 000
1,21 · 0,07 =
1609
104
_
_
..................................................................................................
...............
10
1000
104
1609
167 336
_
..................................................................................................
...............
· _ = _ 10 1000
10 000
16,7336
.................................................................................................. . . . . . . . . . . . . . . .
Het
aantal cijfers na de komma van. . . het
..................................................................................................
............
product
is gelijk aan de som van het aan.................................................................................................. . . . . . . . . . . . . . . .
tal cijfers na de komma van de factoren.
847
7 = _
121 _
·_
= 0,0847
..................................................................................................
.. .. .. .. . . . . . . .
100 100
10 000
Rekenregel – kommagetallen vermenigvuldigen
t Bepaal het teken van het product.
30 · 0,6 · 0,5
t Bereken het product van de getallen zonder komma.
t Plaats de komma in het product.
Het aantal cijfers na de komma van het product is
gelijk aan de som van het aantal cijfers na de komma
van de factoren.
Voeg eventueel nullen vooraan toe als je onvoldoende
cijfers hebt om de komma te plaatsen.
30 · 6 · 5
–1,6 · (–0,9)
= 900
–16 · (–9) = 144
30 · 0,6 · 0,5 = 9
–1,6 · (–0,9)
0,4 · 1,6
–0,07 · 0,8
4 · 16
= 64
0,4 · 1,6
= 0,64
–7 · 8
–0,07 · 0,8
= 1,44
= –56
= –0,056
CONTROLE 47 Reken uit.
2,24 · 0,2 =
0,123 · 0,6 =
b
0,448
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .............................
0,0738
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .............................
1,5 · 7 =
42 · 0,8 =
10,5
.................................................................. . . . . . . . . .. . . . . .
33,6
.................................................................. . . . . . . . . .. . . . . .
Machten van kommagetallen berekenen
t
Vul de tabel aan.
Schrijf als een vermenigvuldiging
Bereken het product
8 2 · _
2 = _
2 · _
2 = _
= 0,008
( _
10 ) 10 10 10 1000
3
(0,2)3
(–0,03)2
3
3
9
= 0,0009
· – _ = _ ( – _
100 ) ( 100 )
10 000
1 · _
1 · _
1 = _
1
1 · _
_
(0,01)
(1,3)2
4
100
100
100 100
100 000 000
= 0,000 000 01
13
169
13 _
_
·
= _ = 1,69
10
10
100
exponent van
de macht
aantal cijfers
na de komma in
het grondtal
aantal cijfers
na de komma in
het product
3
1
3
2
2
4
4
2
8
2
1
2
Als
je het aantal cijfers na de komma
..................................................................................................
..............
in
met de exponent, ken je het aantal cijfers na. .de
. . . . . .het
. . . . . . . . . . grondtal
. . . . . . . . . . . . . . . . . . . . . . . . . . vermenigvuldigt
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......................................................................................................................................
. . . . . . .. . . . . .
komma
in het product.
. . . . . . . . . . . . . . . . . . . . . . .................................................................................................................................................................................................
...............
t
Wat is het verband tussen de laatste drie kolommen?
Rekenregel – macht van een kommagetal
t Bereken de macht van het getal zonder komma.
t Plaats de komma in het resultaat.
0,034
34 = 81
(8 cijfers na de komma, want 2 · 4 = 8)
0,034 = 0,000 000 81
Bereken het aantal cijfers na de komma door de exponent
te vermenigvuldigen met het aantal cijfers na de komma
van het grondtal.
(–0,5)3
(–5)3 = –125
(3 cijfers na de komma, want 1 · 3 = 3)
(–0,5)3 = –0,125
( )
3 3
33
27 Je kunt ook de macht berekenen door het kommagetal eerst 0,033 = _
= _3 =_
= 0,000 027
100
1 000 000
100
te vervangen door een decimale breuk.
CONTROLE 48 Reken uit.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
(0,03)² = .0,0009
0,000 000 008
(–0,002)³ = –
............................................................................
..............
Gebruik van de rekenmachine
Welke toetsen moet je indrukken om (–0,001)2 te berekenen
c
Kommagetallen delen
t
Bereken telkens de gemiddelde
snelheid in km/u.
t
Vul de tabel aan.
bewerking met
kommagetallen
verhouding
verhouding zonder
kommagetallen
(vermenigvuldig
teller en noemer
met eenzelfde macht
van 10)
resultaat in
km/u
Een voetganger legt 17,5 kilometer af
in 3,5 uur.
17,5 : 3,5
Een fietser legt 30,15 kilometer af in
anderhalf uur.
30,15 : 1,5
30,15
_
3015
_
20,1
24 : 0,25
24 _
2400
_
96
Een hogesnelheidstrein rijdt
12 minuten over een traject van
55,2 kilometer.
55,2 : 0,2
55,2
_
552
_
276
Een rolstoelgebruiker doet er
24 minuten over om een helling van
280 meter op te geraken.
0,28 : 0,4
0,28
_
28
_
0,7
Een auto rijdt een afstand van
24 kilometer op een kwartier.
17,5
_
3,5
1,5
0,25
0,2
0,4
175
_
35
150
25
2
40
5
G36
Kommagetallen vermenigvuldigen en delen (vervolg)
t
Hoe kun je op een snelle manier het quotiënt berekenen?
Je
beide getallen
met eenzelfde macht van 10 zodat er geen.. .. .. .. . . . . .
. . . . . . .vermenigvuldigt
. . . . . ....................................................................
................................................................................................................
komma’s
meer voorkomen in deler
en deeltal.
. . . . . . . . . . . . ....................................................................
................................................................................................................
.. .. .. .. . . . . .
Rekenregel – kommagetallen delen
t Vermenigvuldig beide getallen met eenzelfde macht
van tien, zodat er geen komma’s meer voorkomen in
de deler en het deeltal.
–6,4 : (–0,8)
= –64 : (–8)
=8
27 : 0,003
= 27 000 : 3
= 9000
t Pas de tekenregel toe voor het delen van gehele getallen.
0,18 : 0,3
= 18 : 30
= 0,6
–0,28 : 7
= –28 : 700
= –0,04
CONTROLE 49 Reken uit.
–169 : 1300
= . . . .–0,13
........................................
–1,69 : 13 =
–1500 : (–3)
= ......................................
500
–15 : (–0,03) =
............................................
428 : 40
= ..............................
10,7
. . . . . . . . .. . . . .
4,28 : 0,4 =
......................................
.............................. . . . . . . . . .. . . . .
Oefeningen
WEER?
470
WEER?
471
WEER?
472
14 t
t
Reken uit.
Schat eerst het resultaat.
a
0,21 · 0,3 =
0,063
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
d
1,1 · (–0,3) · 20 =
–6,6
.................................................. . . . . . . . . .. . . . . .
b
–2,3 · (–0,001) = 0,0023
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
e
–0,7 · (–0,014) =
0,0098
.................................................. . . . . . . . . .. . . . . .
c
–1,2 · 4 =
–4,8
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
f
5 · (–0,07) · (–0,2) =
0,07
.................................................. . . . . . . . . .. . . . . .
15 t
t
Reken uit.
Schat eerst het resultaat.
a
0,014 =
0,000
. . . . . . . . . . . . . . . . . 000
. . . . . . . . . . . . .01
..........
c
0,034 =
.........................................
0,000 000 81
e
(0,004)3 =
0,000
000. . .064
..........................
............
b
8,241 =
8,24
........................................
d
(0,14)2 =
.........................................
0,0196
f
(2,04)0 =
1.......................... . . . . . . . . . . . . . . .
.......................................
–1,21
e
–0,0032 =
..........................
...............
–0,000
009
f
–0,72 =
......................... . . . . . . . . .. . . . . . .
–0,49
16 t
t
Reken uit.
Schat eerst het resultaat.
a
(–0,002)3 = –0,000
. . . . . . . . . . . . . . . . 000
. . . . . . . . . .008
......
c
–1,12 =
b
(–1,5)2=
2,25
d
– (–0,02)5 = 0,000
.......................................
000 003 2
17 t
t
a
................................
Reken uit.
Schat eerst het resultaat.
4,5 : 0,09 =
WEER?
473
450
. . . . . . . . . . . .:. . .9
. . . . . . . . . . . . . . . . . . . . . . . . . . .........................
d
15,3 : 0,0003 =
=
. . . . . . . . 50
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
b
36 : (–0,6) =
360
. . . . . . . . . . . .:. . .(–6)
. . . . . . . . . . . . . . . . . . . . . . . . . . .........................
=
51 000
...................................................
...............
e
0,005 : 0,2 =
=
. . . . . . . . –60
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
c
–1,44 : (–1,2) = –144
. . . . . . . . . . . . . . .:. . .(–120)
. . . . . . . . . . . . . . . . . . . . . . . .........................
=
. . . . . . . . 1,2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
153
000 : 3
...................................................
. . . . . . . . .. . . . . .
5....................................................
: 200
..............
=
0,025
...................................................
...............
f
0,48 : 6 =
48
: 600
....................................................
..............
=
0,08
....................................................
..............
18 t
t
a
Reken uit.
Noteer de tussenstappen.
2 · 0,7 =
–_
3
b
7 –2 · _
= _
3 10
–2 · 7 = _
3·2·5
–7 = _
15
19 t
t
WEER?
474
–7 – 1,2 =
3,24 + _
4
c
1 =
0,6 : _
5
= 3,24 – 1,75 – 1,2
= 0,6 : 0,2
= 0,29
= 6:2
= 3
WEER?
477
Schat het resultaat.
Omcirkel de juiste oplossing
a
36,7 · 2,24 =
822,08
82,208
8,2208
b
42,12 : 5,2 =
8,1
81
0,81
c
3,98 + 6,17 + 2,9 =
13,05
11,93
14,23
d
70,12 – 59,87 =
11,75
129,99
10,25
20 Rekenen met wisselkoersen.
a
b
c
MEER?
475
476
Sara wil op reis naar Australië. Hoeveel Australische
dollar krijgt ze van de bank als ze € 750 wil omwisselen?
Na haar reis heeft Sara nog 125 Australische dollar
over. Ze gaat deze dollars inruilen tegen euro’s.
Hoeveel euro krijgt ze hiervoor van de bank?
Hoeveel verlies heeft Sara geleden door te veel euro
in Australische dollar te laten omwisselen?
750 · 1,5650 = 1173,75
Ze krijgt 1173,75 Australische dollar . . . . . . . . . . . . . .
....................................................................................................
WEER?
480
481
125 : 1,7007 = 73,4991474
MEER?
482
483
.................................................................................................... . . . . . . . . . . . . . .
Ze krijgt 73,50 euro van de bank.
.................................................................................................... . . . . . . . . . . . . . .
125 : 1,5650 = 79,8722045
.................................................................................................... . . . . . . . . . . . . . .
79,87 – 73,50 = 6,37
.................................................................................................... . . . . . . . . . . . . . .
Wisselkoersen voor 1 EUR
munt
aankoop
verkoop
Amerikaanse dollar
1,2829
1,3859
Australische dollar
1,5650
1,7007
Britse pond
0,6548
0,6985
Canadese dollar
1,4962
1,5975
Deense kroon
7,2020
7,6899
Noorse kroon
7,8684
8,4347
Zweedse kroon
8,9163
9,6360
Zwitserse frank
1,5817
1,6797
MEER?
478
479
Sara heeft 6,37 euro verlies geleden.
.................................................................................................... . . . . . . . . . . . . . .
Voorbeeld: Als je van de bank Amerikaanse
dollarbiljetten koopt, dan krijg je voor
1 euro 1,2829 USD. Als je Amerikaanse
dollarbiljetten verkoopt aan de bank, dan
krijg je voor 1,3859 USD maar 1 euro.
Wat moet je kunnen?
τ kommagetallen vermenigvuldigen (met je rekenmachine)
τ kommagetallen delen (met je rekenmachine)
τ de macht van een kommagetal berekenen (met je rekenmachine)












