uitwerkingen opgaven les 14

VERON TWENTE ZENDCURSUS 2013 – UITWERKINGEN OPGAVEN LES 14
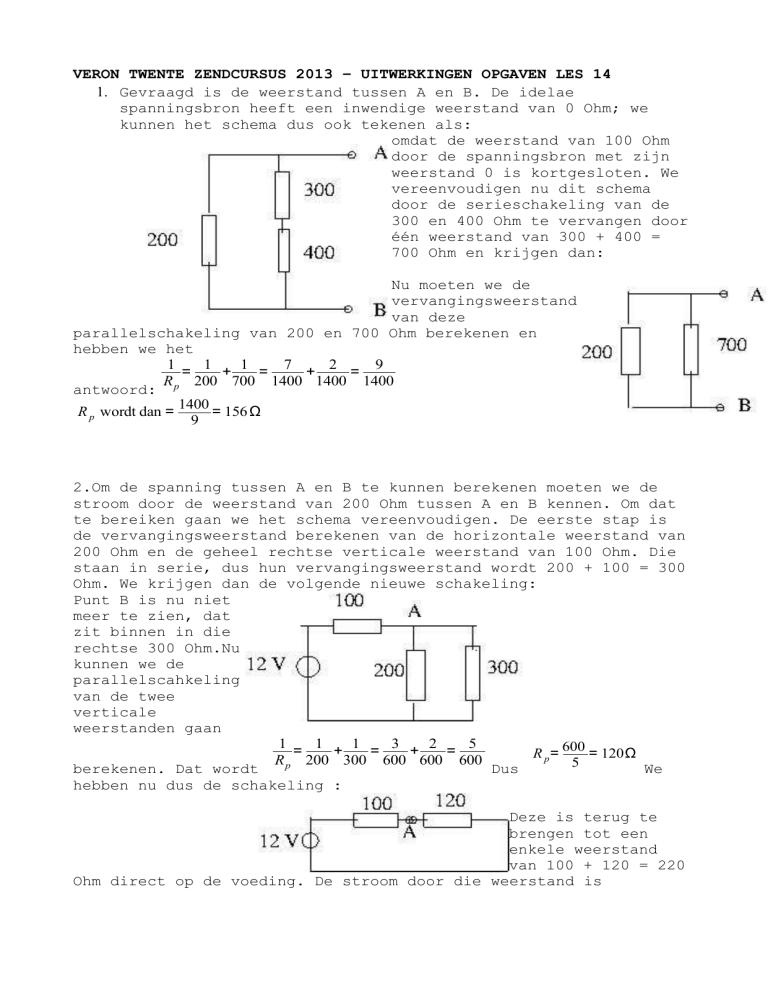
1. Gevraagd is de weerstand tussen A en B. De idelae
spanningsbron heeft een inwendige weerstand van 0 Ohm; we
kunnen het schema dus ook tekenen als:
omdat de weerstand van 100 Ohm
door de spanningsbron met zijn
weerstand 0 is kortgesloten. We
vereenvoudigen nu dit schema
door de serieschakeling van de
300 en 400 Ohm te vervangen door
één weerstand van 300 + 400 =
700 Ohm en krijgen dan:
Nu moeten we de
vervangingsweerstand
van deze
parallelschakeling van 200 en 700 Ohm berekenen en
hebben we het
1
1
1
7
2
9
=
+
=
+
=
R p 200 700 1400 1400 1400
antwoord:
1400
R p wordt dan =
= 156 Ω
9
2.Om de spanning tussen A en B te kunnen berekenen moeten we de
stroom door de weerstand van 200 Ohm tussen A en B kennen. Om dat
te bereiken gaan we het schema vereenvoudigen. De eerste stap is
de vervangingsweerstand berekenen van de horizontale weerstand van
200 Ohm en de geheel rechtse verticale weerstand van 100 Ohm. Die
staan in serie, dus hun vervangingsweerstand wordt 200 + 100 = 300
Ohm. We krijgen dan de volgende nieuwe schakeling:
Punt B is nu niet
meer te zien, dat
zit binnen in die
rechtse 300 Ohm.Nu
kunnen we de
parallelscahkeling
van de twee
verticale
weerstanden gaan
1
1
1
3
2
5
600
=
+
=
+
=
R p=
= 120Ω
R p 200 300 600 600 600
5
berekenen. Dat wordt
Dus
We
hebben nu dus de schakeling :
Deze is terug te
brengen tot een
enkele weerstand
van 100 + 120 = 220
Ohm direct op de voeding. De stroom door die weerstand is
I=
U 12
=
= 0,0545 A
R 220
.We zijn nu in staat om de spanning op punt A te
berekenen: die is 12V minus de spanningsval over de weerstand van
Ohm bij de berekende stroom van 0,0545 A dus 0,0545 * 100 = 5,45
V. De spanning op A is dus 12 – 5,45 = 6,55 V. Gaan we nu terug
naar de figuur met de 200 en 300 Ohm parallel. We kunnen daar nu
de stroom door de rechtse weerstand van 300 Ohm uitrekenen omdat
U 6,55
I= =
= 0,022 A .
R 300
we de spanning op A kennen:
Tenslotte gaan we terug
naar de eerste figuur en zien dat die stroom door de weerstand van
200 Ohm tussen A en B loopt. De spanningsval over die weerstand is
de gevraagde spanning tussen A en B en is te berekenen met
U AB =I∗ R= 0,022∗ 200= 4,4 V
3. Een som waar zowel negatieve als positieve spanningen op
bepaalde punten in de schakeling gegeven zijn, pakken we aan door
alle spanningen tijdelijk te verschuiven met het zelfde bedrag en
na alle berekeningen schuiven we de spanningen weer met hezelfde
bedrag terug. Die verschuiving doen we door bij alle gegeven
spanningen een spanning gelijk aan de absoukte waarden van de
meest negatieve spanning op te tellen. In dit geval is het meest
negatieve punt in de schakeling -5 V. We tellen dus overal 5 V bij
op en krijgen dan:
deze schakleing is te
vereenvoudigen door de
serieschakeling van de twee
weerstanden te vervangen door
één enkele weerstand van 10 + 15
= 25 k. De stroom door die
weerstand wordt
U 25
I= =
= 0,001 A
R 25000
dus:
Teruggaand
naar de figuur met twee
weerstanden kunnen we nu de
spanning op A uitrekenen
U =I∗ R=0,001∗ 10000= 10V
met A
. Nu
hebben we nog niet het
eindantwoord want we moeten de
spanning nog terugschuiven. We
hadden de spanningen eerst mt 5
V opgehoogd, nu dus met 5 V verlagen geeft
u a= 10− 5= 5V
4. We gaan deze schakeling vereenvoudigen door eerst de twee
parallel geschakelde weerstand van 1 k en 10 k te vervangen door
1
1
1
10
1
11
1
=
+
=
+
=
= 0,0011
R p=
= 909Ω
R p 1000 10000 10000 10000 10000
0,0011
Rp:
Dus
We
krijgen dan dus
Deze serieschakeling kunnen we vervangen door één
enkele weerstand met de waarde 1000 +10000 + 909=
11909 Ω. Daarmee kunnen de de stroom door die
U 10
I= =
= 0,00084 A
R 11909
weerstand berekenen:
De
gevraagde spanning volgt nu
U =I∗ R=0,00084∗ 909= 0,76 V
uit: A
5. We moeten de stroom door R zien te vinden. We gaan alle
paralle
lschake
lingen
van
weersta
nden
vervang
en en
krijgen
dan
1
1 1 2
= + =
R p1=
R p1 5 5 5
1
1 1
2
= + =
R p2 10 10 10
R p2 =
10
= 5Ω
2
1
1 1
2 1
3
= + = + =
R p3 5 10 10 10 10
R p3=
10
= 3,3 Ω
3
We
hebben
nu dus
Dit
schema
gaan we
ook
weer
vereenv
oudigen
door de twee takken met serieweerstanden te vervangen door enkele
weerstanden:
tenslotte vereenvoudigen we dit tot een enkele weerstand Rtotaal
1
1
1
1
=
+
= 0,164 R Ptotaal=
R ptotaal 22,5 8,33
0,164
R Ptotaal=
1
= 6Ω
0,164
We kunnen nu de
spanning over de uiteinden van de schakeling berekenen:
U totaal =I∗ R=0,1∗ 6= 0,6V
Gaan we nu naar de vorige tekening, dan kunnen
we de stroom in de onderste tak berekenen met
U 0,6
I onder = =
= 0,072 A
R 8,33
. We keren nu terug naar de figuur met de 4
weerstanden. De I in de onderste tak is dus 0,072 A, de spanning
over de 3,33 Ω weerstand is dus U=I∗ R=0,072∗ 3,33= 0,24V . Nu gaan we
naar de oorspronkelijke schakeling: we weten nu dat de spanning
over de 5 Ohm weerstand R gelijk is aan 0,24V en kunnen nu de
U 0,25
I= =
= 0,048 A = 48 mA
R
5
stroom door die weerstand berekenen
6. De dissipatie in R1 is 10 W. Daarmee kunnen we de stroom door
10
P=I 2∗ R invullen geeft 10 =I 2∗ 10 dus I 2 = = 1
10
R1 berekenen
1= 1A . De stroom door de hele tak met R1 erin is dus 1 A.
Dus I= √
we vereenvoudigen nu het schema
Rs = 10 + 10 = 20 Ώ. De spanning over Rs is dus U=I∗ R=1∗ 20= 20 V
dat is ook de spanning over de bovenste tak. De weerstand van 5
U 2 20∗ 20 400
P=
=
=
= 80 W
R
5
5
Ohm dissipeert dus
. R2 heeft dezelfde waarde
als R1 en er gaat ook dezelfde stroom door. R2 dissipeert dus ook
10 W
7. We beginnen met de schakeling te vereenvoudigen door de twee
parallele zelfinducties te vervangen door één enkele
1 1 1 3 1
4
15
= + = + =
L p = = 3,75 mH
L p 5 15 15 15 15
4
Lp
dus
We krijgen dan
Van deze serieschakeling rekenen we de totale zelfinductie uit
door de twee op te tellen. De totale
zelfinductie is dan 13,75 mH.
8.We beginnen de vereenvoudiging bij de twee parallele C's en
krijgen dan
met
C p= 4+1= 5 μF
; vervolgens vervangen we de serieschakeling van de
1
1 1 1 1 2 2
5
10
=
+ + =
+ + =
C s = = 2 μF
C s 10 5 5 10 10 10 10
5
drie C's door Cs met
Dus