Elektriciteitsleer Inwendige weerstand Een batterij heeft een

Elektriciteitsleer
Inwendige weerstand
Een batterij heeft een bronspanning van 1,5 V en een inwendige weerstand van 3,0 .
a.
Teken de grafiek van de klemspanning als functie van de stroomsterkte. Let er wel op dat
de schaal voldoende groot gekozen wordt. Een spanningsas van minimaal 7,5 cm. Ook de
stroomas moet voldoende lang zijn: meer dan 7 cm.
Een weerstand van 2,0  wordt aangesloten op de klemmen van de batterij.
b.
Teken in hetzelfde assenstelsel de grafiek van een weerstand van 2,0 .
c.
Bepaal het door deze weerstand opgenomen vermogen.
d.
Toon aan dat een weerstand van 4,5  eenzelfde vermogen opneemt.
e.
Beredeneer of bij gebruik van een weerstand tussen 2,0 en 4,5  als uitwendige
weerstand het opgenomen vermogen groter is of kleiner of misschien wel hetzelfde.
a.
b.
c.
d.
e.
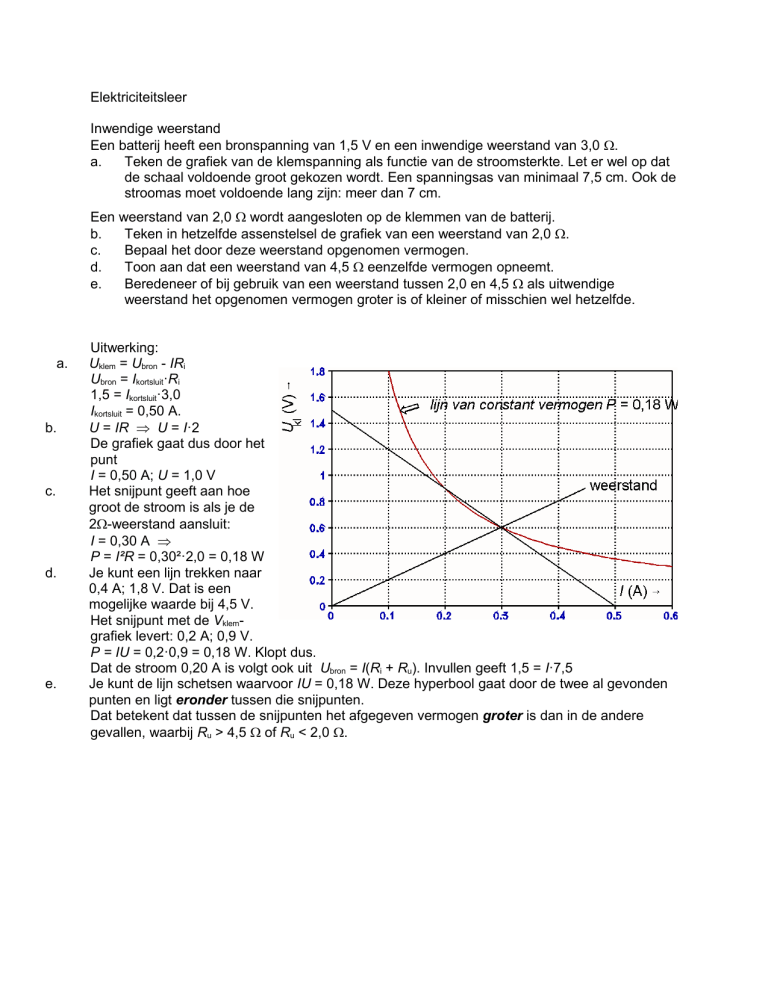
Uitwerking:
Uklem = Ubron - IRi
Ubron = Ikortsluit·Ri
1,5 = Ikortsluit·3,0
Ikortsluit = 0,50 A.
U = IR  U = I·2
De grafiek gaat dus door het
punt
I = 0,50 A; U = 1,0 V
Het snijpunt geeft aan hoe
groot de stroom is als je de
2-weerstand aansluit:
I = 0,30 A 
P = I²R = 0,30²·2,0 = 0,18 W
Je kunt een lijn trekken naar
0,4 A; 1,8 V. Dat is een
mogelijke waarde bij 4,5 V.
Het snijpunt met de Vklemgrafiek levert: 0,2 A; 0,9 V.
P = IU = 0,2·0,9 = 0,18 W. Klopt dus.
Dat de stroom 0,20 A is volgt ook uit Ubron = I(Ri + Ru). Invullen geeft 1,5 = I·7,5
Je kunt de lijn schetsen waarvoor IU = 0,18 W. Deze hyperbool gaat door de twee al gevonden
punten en ligt eronder tussen die snijpunten.
Dat betekent dat tussen de snijpunten het afgegeven vermogen groter is dan in de andere
gevallen, waarbij Ru > 4,5  of Ru < 2,0 .
INWENDIGE WEERSTAND
Bij deze opgave gebruiken we twee voltmeters; een is ideaal en geven we aan met Vid en de
andere is er een met een meterweerstand van 20 k en die geven we aan met V20.
Beide hebben een meetbereik van 100 V.
De gebruikte voeding geeft een constante spanning van 100 V af.
Leid in elk van de onderstaande schakelingen af, hoe groot de door de meters aangegeven
spanning is. Zorg dat duidelijk is over welke schakeling je het hebt.
A.
B.
C.
D.
UITWERKING:
Door de 20 en 30  loopt dezelfde stroom: spanningsdeler.
Verhouding 20:30 = 40:60. De ideale voltmeter geeft 40 V aan.
De stroom door de voltmeter is verwaarloosbaar. De voltmeter met Rmeter = 20 k is als ideaal te
beschouwen en geeft dus eveneens 40 V aan.
Zie A. De voltemeter geeft 40 V aan.
De ideale voltmeter kun je eerst wegdenken. Die speelt in het begin van de redenering geen rol.
De andere voltmeter kun je vervangen denken door een weerstand van 20 k. Er zijn dus twee
weerstanden van 20 k parallel geschakeld. Hun vervangingsweerstand is 10 k. Je hebt dus
een spanningsdeler met de verhouding 10:30 = 25:75. De meter V20 geeft dus 25 V aan en de
andere de rest dus Vid geeft 75 V.
a.
b.
c.
Inwendige weerstand
Een batterij met een bronspanning van 9,0 V heeft een inwendige weerstand van 0,9 .
Teken van deze batterij de (Vklem,I)-grafiek.
Ik wil er een weerstand op aansluiten, zodat Vklem= 6,0 V wordt.
Bepaal hoe groot de waarde van die aangesloten weerstand dan moet zijn.
Bereken hoeveel energie de batterij per kwartier aan die weerstand levert. Als je het antwoord
op de vorige vraag niet hebt kunnen berekenen, veronderstel dan dat daar 5,1  uit gekomen
zou zijn.
Een batterij met een een bronspanning van 9,0 V en een inwendige weerstand van 1,5  wordt
gebruikt om energie te leveren aan een weerstand van 3,0 .
a.
Bepaal grafisch de spanning over de weerstand van 3,0 . 'Bepaal grafisch' wil zeggen
dat de essentie van de oplossing moet liggen in het gebruik van grafieken.
b.
Bereken het door die weerstand opgenomen vermogen.
a.
b.
c.
d.
e.
RI EN RU
Op een 12V-accu wordt een regelbare weerstand
aangesloten.
In het begin is de inwendige weerstand van deze accu
2,0 .
We variëren de uitwendige weerstand en meten zo de
klemspanning als functie van de stroomsterkte.
Teken de grafiek van de klemspanning Vkl als functie van
de stroomsterkte in het rechtdeel van de onderstaande
grafiek.
Bereken de stroomsterkte en de klemspanning als een uitwendige weerstand van 2,0  wordt
aangesloten. En geef de resultaten in de linker en rechter grafiek weer.
Schets het linkerdeel van de grafiek, dus de (Vklem,Ru)-grafiek.
Bereken het door de uitwendige weerstand van 2,0  opgenomen vermogen.
Bij een uitwendige weerstand van 10  is dat vermogen 10 W.
Teken in het rechter assenstelsel de grafiek die overeenkomt met P = 10 W.
f. Bereken hoe lang het duurt voordat deze weerstand een energie van 0,010 kWh heeft
opgenomen.
UITWENDIGE WEERSTAND
Op een batterij met een bronspanning van 12,0 V wordt een regelbare weerstand aangesloten,
de uitwendige weerstand Ru. Als functie van de uitwendige weerstand wordt de stroomsterkte
en de klemspanning gemeten.
Van beide zijn de metingen grafisch weergegeven in bijgaande grafiek.
a.
b.
Bepaal de waarde van de inwendige weerstand van de batterij.
Bepaal het aan Ru geleverde vermogen, als Ru = 1,0 .
c.
De regelbare weerstand is van een type dat geen groter vermogen dan 8 W kan verwerken.
Bepaal de grenzen waartussen je de uitwendige weerstand mag variëren zonder het risico te
lopen, dat deze kapot gaat.
a.
b.
c.
Uitwerking:
Uit de grafiek blijkt dat de kortsluitstroom
12 A is.
Ubron = Ikort·Ri  12 = 12·Ri  Ri = 1,0 .
Als Ru = 1,0 , blijkt Uklem = 6,0 V en I =
6,0 A, zodat P = IV = 6,0·6,0 = 36 W.
Als het vermogen niet groter mag zijn dan
8 W, moet je gaan kijken waar het product
boven de 8 komt. Dat is even puzzelen. Een
andere aanpak is dat je middels een paar
punten de grafiek tekent van het afgegeven
vermogen als functie van de uitwendige
weerstand. Je krijgt dan de onderstaande
grafiek. De waarde van het vermogen mag
niet boven de 8 W komen, en dus moet Ru < 0,1  of Ru > 16 .
Commentaar: Voor de kleine waarde van Ru loopt weliswaar de uitwendige weerstand geen
gevaar, maar de voeding des te meer. De stroomsterkte wordt bepaald door Ri en is dus 12 A.
Dan moet P = I²R, zodat 8 = 12²·Ru  Ru = 0,06 .
Voor de computerfreaks en wiskundigen: op basis van deze Ru kun je weer een betere schatting
van I maken. Dit levert dan een beter schatting op van Ru. Op basis van deze Ru kun je
weer......... Dit heet de iteratieve methode.
a.
SCHAKELEN
Van een lamp is bijgaande
karakteristiek gemaakt. Zie
onderaan. De lamp wordt
aangesloten op de klemmen
van een voeding. Van deze
voeding is bekend dat de
bronspanning 3,0 V is en de
inwendige weerstand 0,20 
(variant: 0,30 ).
Bepaal op welke spanning
de lamp 'brandt'.
c.
Je krijgt de beschikking over
twee van dergelijke
voedingen. Daarmee bestaat
de mogelijkheid om de lamp
feller te laten branden. Je
overweegt twee
mogelijkheden:
(I)
Je schakelt de twee
voedingen parallel.
(II) Je schakelt de twee
voedingen in serie.
Beredeneer waar je voor zult
kiezen.
Teken de schakeling van je keuze.
d.
De gekozen combinatie van twee voedingen beschouwen we als een geheel met klemmen
P en Q.
Teken van deze combinatie de (UPQ,I)-grafiek in de grafiek.
b.
Uitwerking:
Als een stroom van 6,0 A loopt door de voeding betekent dat een inwendig spanningsverlies
van I·Ri = 6,0·0,20 = 1,2 V. In de andere versie 1,8 V.
We kunnen dan de grafiek tekenen van Vklem als functie van I.
a.
b.
Het snijpunt bepaalt de gevraagde spanning. Resp. 2,3 en 2,1 V.
Als de lamp feller moet branden, moet er meer stroom door.
Door ze in serie te schakelen tel je de bronspanningen op. De inwendige weerstand verdubbelt
dan ook. Maar niet de weerstand van de lamp. De stroom zal dus toenemen een de lamp zal
feller branden.
Door ze parallel te schakelen, hoeft elke voeding slechts de helft van de totale stroom te
leveren. Het inwendig spanningsverlies is dan de helft, zodat er voor de lamp meer over blijft.
De lamp zal feller branden.
c.
c.
Zie
grafieken. Uit de
grafieken blijkt dat
bij
parallelschakeling
de
stroomtoename
groter is.
Als je wilt dat de
lamp feller brandt
is dat het
effectiefst.
Serie:
Vbron = 6,0 V en
Ri = 0,4  resp.
0,6 ;
Ikortsluit = 15 resp.
10 A.
Parallel:
Vbron = 3,0 V en
Ri = 0,1  resp.
0,15 ;
Ikortsluit = 30 resp.
20 A.
a.
b.
c.
d.
VARIANT
Een spanningsbron met een
bronspanning van 6,0 V heeft
een inwendige weerstand van
4,0 .
Er wordt een lamp op
aangesloten met bijgaande
(I,V)-karakteristiek.
Bepaal de spanning waarop de
lamp brandt.
In plaats van de lamp wordt in
de stroomkring een
schuifweerstand met een
bereik van 0 tot 100 
opgenomen.
Bereken de waarde van Ru,
waarbij Vklem = 5,5 V.
Schets de grafiek van de
klemspanning als functie van
de Ru; 0<Ru<100 
De spanningsbron wordt
vernield als de stroomsterkte
door de bron meer dan 300 mA
bedraagt. Bepaal de minimale
waarde van Ru.
Uitwerking:
a. Een batterij met een bronspanning van 6,0 V en een inwendige weerstand van 4,0  heeft
een kortsluitstroom van 1,5 A volgens V = I·R.
De grafiek van de klemspanning als functie van de stroomsterkte is getekend. Waar deze
grafiek die van de lamp snijdt, heb je de stroom en spanning die bij de aangesloten lamp horen:
0,75 V
b. Het inwendig spanningsverlies is 0,5 V, dus IRi = 0,5  I = 0,125 A
Met Vklem = IRu volgt 5,5 = 0,125·Ru  Ru = 44 .
c. Je kent nu een punt van de gevraagde grafiek.
Andere punten kun je vinden door telkens een andere waarde voor I te kiezen.
Eerst Vklem = Vbron - IRi. Iedere I lvert een Vklem en dan Vklem = IRu levert de bijbehorende Ru.
Ook kun je starten met 6,0 = I(4,0 + Ru).
Kies een Ru, dat levert I en dan Vklem = IRu.
De grafiek is er in geschetst. De waarden van Ru staan bovenaan.
d. De stroom mag niet boven de 300 mA uit komen. Dus uit Vbron = I(Ri + Ru)
6,0 = 0,300·(4,0 + Ru) volgt dat Ru > 14  moet zijn.
METERAANPASSING
Je weet dat je door weerstanden in serie of parallel te schakelen het meetbereik van een meter
kunt veranderen.
Gegeven is een stroommeter met een meetbereik van 1 mA. Deze meter heeft een weerstand
van 150 . Zie de linker tekening.
Bereken het meetbereik als een weerstand van 2,85 k in serie wordt geschakeld, zoals in de
rechter tekening.
Uitwerking”
De wijzer slaat volledig uit, zoweel in de oude als in de nieuwe situatie als er een stroom van
1 mA van het ene naar het andere aansluitpunt stroomt. Vanuit die optiek blijft het een meter
met een bereik van 1 mA. Alleen een slechtere.
Alleen sluit je een weerstand in serie aan met de bedoeling er een voltmeter van te maken.
De totale weerstand tussen de aansluitpunten is 2,85 + 0,150 = 3,00 k.
Daardoor is V = I·R = 0,001 · 3000 = 3,0 V. Het meetbereik is dus 3 V.
STROOMKRINGEN GEKOPPELD
a.
b.
Getekend zijn twee kringen los van elkaar.
De punten P en Q worden met elkaar verbonden. De schakelaar S staat open.
Bepaal de potentiaal in de punten A, B en C.
De schakelaar wordt gesloten.
Bepaal de potentiaal in de punten A,
B en C.
De schakelaar blijft gesloten, maar
niet punt A wordt geaard, maar
punt B.
c. Bepaal de potentiaal in de punten A, B en
C.
KLEMSPANNING
Niet op examen
Sluiten we op een voeding van 9,0 V een weerstand aan van 10,3 , dan blijkt de klemspanning
8,5 V te zijn.
Bepaal of bereken de waarde van de inwendige weerstand van de voeding.
KLEMSPANNING
Niet op examen
Drie oplaadbare penlight-batterijen (elk Ubron = 1,2 V; Ri = 0,6 ) worden parallel geschakeld.
Hierop wordt een weerstand van 2,2  aangesloten.
A.
Bereken de klemspanning van de batterijen.
De stroom door de aangesloten weerstand blijkt gedurende 60 minuten niet noemenswaard te
veranderen.
B.
Bereken hoeveel energie er dan minstens in de batterijen opgeslagen was.
C
De klemspanning van vraag A wil men meten met een voltmeter.
Maak een schatting van de weerstand die de voltmeter moet hebben en beargumenteer je
schatting.
INWENDIGE WEERSTAND In deze vorm geen examenonderwerp
Op een batterij met een bronspanning van 9,0 V en een inwendige weerstand van 1,0  wordt
een weerstand aangesloten van 8,0 .
Bereken het door die uitwendige weerstand opgenomen vermogen.
Bereken of bepaal bij welke waarde van de uitwendige weerstand eveneens datzelfde
vermogen uitwendig wordt opgenomen.
b.
Uitwerking:
Gegeven is dat R = 8,0 .
Om uit te rekenen hoe groot het opgenomen vermogen is -- en dat kun je uitrekenen met P =
I²R -- moet je weten hoe groot de stroom is door die weerstand. De stroomsterkte kun je
uitrekenen met de wet van Ohm. U = IR  9,0 = I × (1,0 + 8,0)
 I = 1,0 A.
P = I²R = 1,0² × 8.0 = 8,0 W.
Je moet nu dezelfde berekening maken maar dan
zonder 8,0  in te vullen.
U = IR × 9,0 = I × (1,0 + R) 
I
9,0
1,0  R .
2
 9,0 
8,0  
  R  R  0,125 
 1,0  R 
P = I²R 
en
dus geef je als antwoord R = 0,13 .
Je moet wiskundig sterk genoeg zijn om dit uit te
rekenen.
Dat gaat zo, maar het kan ook anders:
81


2
2
8 
2   R  8  16 R  8 R  81R  8 R  65R  8  0
 1  2R  R 
.
Het is tijd voor de abc-formule. Die geeft twee antwoorden: R = 8 , maar die kennen we al.
Bovendien R = 0,125  en dat is de andere waarde waar we naar op zoek waren.
Uit het woord bepaal mag je afleiden dat je dit ook met een grafiek had kunnen oplossen. Maar
welke? Er zijn twee gegevens. De eerste dat het vermogen 8,0 W is en dan dat we te maken
hebben met een batterij met bronspanning 9,0 V en inwendige weerstand van 1,0  en dus
kortsluitstroom van 9,0 A.
Als je weet dat de maximale vermogens overdracht plaatsvindt indien Ru = Ri = 1,0 . Als de
ene oplossing ligt bij 8 , moet de ander evenveel aan de andere kant liggen van 1,0 
vanwege de symmetrie in de vergelijkingen tussen Ri en Ru. De stap die je nog moet zetten is
niet 7 naar links maar i.p.v. vermenigvuldigen met 8, delen door 8 en dus 1/8 .