Afgeleiden van inverse goniometrische functies: f(x) Domein Bereik f

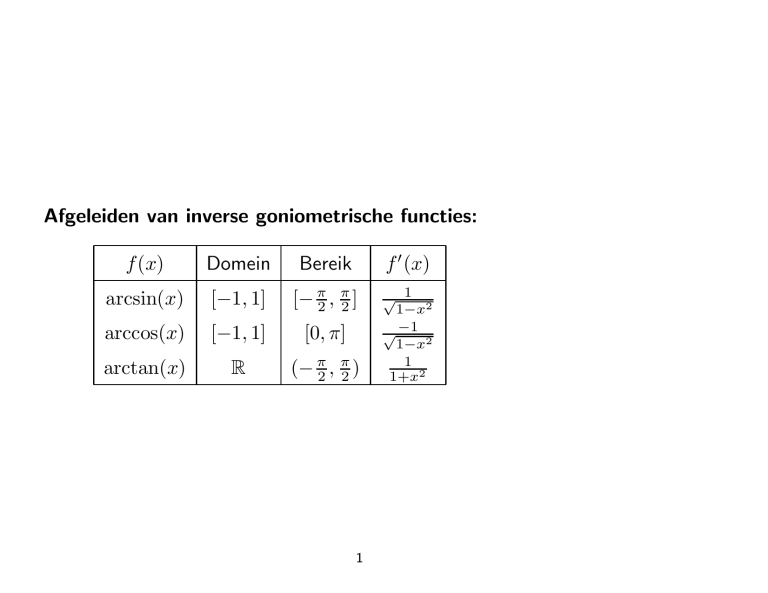
Afgeleiden van inverse goniometrische functies:
f (x)
Domein
Bereik
f 0 (x)
arcsin(x)
[−1, 1]
[− π2 , π2 ]
arccos(x)
[−1, 1]
[0, π]
arctan(x)
R
(− π2 , π2 )
√ 1
1−x2
√ −1
1−x2
1
1+x2
1
Middelwaardestelling:
Veronderstel dat de functie f continu is op het gesloten begrensde interval
[a, b], en differentieerbaar op het open interval (a, b). Dan bestaat er een
punt c ∈ (a, b) zó dat
f (b) − f (a)
= f 0 (c).
b−a
2
Definitie: Zij f een functie gedefinieerd op een interval I.
(a) Als f (x2 ) > f (x1 ) voor x2 > x1 dan f (strikt) stijgend op I,
(b) Als f (x2 ) < f (x1 ) voor x2 > x1 dan f (strikt) dalend op I,
(c) Als f (x2 ) ≥ f (x1 ) voor x2 > x1 dan f niet dalend op I,
(d) Als f (x2 ) ≤ f (x1 ) voor x2 > x1 dan f niet stijgend op I.
Stelling: Zij J een open interval, en I de afsluiting van J.
(a) Als f 0 (x) > 0 voor alle x ∈ J, dan f stijgend op I,
(b) Als f 0 (x) < 0 voor alle x ∈ J, dan f dalend op I,
(c) Als f 0 (x) ≥ 0 voor alle x ∈ J, dan f niet dalend op I,
(d) Als f 0 (x) ≤ 0 voor alle x ∈ J, dan f niet stijgend op I.
3
Stelling: Zij f gedefinieerd op een open interval (a, b), en veronderstel dat
f een maximum (of een minimum) aanneemt in het punt c ∈ (a, b). Als
f 0 (c) bestaat, dan f 0 (c) = 0.
Stelling van Rolle: Zij g continu op [a, b] en differentieerbaar op (a, b).
Als g(a) = g(b), dan is er een punt c ∈ (a, b) zó dat g 0 (c) = 0.
4
Exponentiële functies
Voor a > 0, n ∈ N, en m ∈ Z\{0} geldt:
a0
=
1,
an
=
a−n
=
am/n
=
a · a · a · · · a, (n factoren)
1
,
an
√
n
am .
Voor reële getallen x wordt de definitie als volgt uitgebreid:
ax =
lim
r→x,r∈Q
ar .
De functie f (x) = ax heeft R als domein, en (0, ∞) als bereik (mits a 6= 1).
5
Rekenregels:
Als a > 0 en b > 0, en x, y ∈ R, dan geldt
1. a0 = 1,
2. ax+y = ax ay ,
3. a−x =
1
ax ,
4. ax−y =
ax
ay ,
5. (ax )y = axy ,
6. (ab)x = ax bx .
• Als a > 1, dan limx→−∞ ax = 0 en limx→∞ ax = ∞,
• Als 0 < a < 1, dan limx→−∞ ax = ∞ en limx→∞ ax = 0,
6
Logaritmen:
Definitie: Als a > 0 en a 6= 1, dan is de functie a log x, d.w.z. de
logaritme van x t.o.v. basis a, gedefinieerd als de inverse functie van de
injectieve functie ax :
y = a log x ⇐⇒ x = ay .
Het domein van de logaritme is (0, ∞), het bereik is R. Er geldt:
• Voor alle x ∈ R:
a
log ax = x,
a
• Voor all x > 0: a log x = x.
7
Rekenregels voor logaritmen:
Voor x > 0, y > 0, a > 0, en b > 0, met a 6= 1 en b 6= 1 geldt:
(i)
a
log 1 = 0,
(ii)
a
log(xy) = a log x + a log y,
(iii)
a
log
1
x
= − a log x,
(iv)
a
log
x
y
= a log x − a log y,
(v)
a
log xy = y a log x,
(vi)
a
b
log x =
log x
.
b
log a
8
Limieten van logaritmen:
Als a > 1, dan geldt
• limx↓0 a log x = −∞,
• limx→∞ a log x = ∞.
Als 0 < a < 1, dan geldt
• limx↓0 a log x = ∞,
• limx→∞ a log x = −∞.
9
De e-macht:
Definitie:
lim
n→∞
1
1+
n
n
= e.
Hieruit volgt voor iedere x ∈ R:
x n
= ex .
lim 1 +
n→∞
n
Beschouw de functie exp(x) = ex , dan geldt
• Domein(exp) = R,
• Bereik(exp) = (0, ∞).
Standaardlimiet:
eh − 1
= 1.
lim
h→0
h
10
Rekenregels voor de e-macht:
Voor x, y ∈ R geldt
1. exp(0) = 1,
2. exp(x + y) = exp(x) · exp(y),
3. exp(−x) =
1
exp(x) ,
4. exp(x − y) =
exp(x)
exp(y) ,
5. exp(xy) = (exp(x))y ,
11
De natuurlijke logaritme:
De natuurlijke logaritme ln is de inverse van de exponentiële functie exp:
y = exp(x) ⇐⇒ x = ln y (y > 0).
Er geldt dus
• Domein(ln) = (0, ∞),
• Bereik(ln) = R.
In het bijzonder
• Voor alle x ∈ R: ln(exp(x)) = x,
• Voor alle x > 0: exp(ln x) = x.
Standaardlimiet:
ln(1 + h)
= 1.
lim
h→0
h
12
Rekenregels voor de natuurlijke logaritme:
Voor x > 0 en y > 0 geldt:
(i) ln 1 = 0,
(ii) ln(xy) = ln x + ln y,
(iii) ln x1 = − ln x,
(iv) ln xy = ln x − ln y,
(v) ln xy = y ln x,
13
Limieten:
(i) limx→∞ exp(x) = ∞,
(ii) limx→−∞ exp(x) = 0,
(iii) limx↓0 ln x = −∞,
(iv) limx→∞ ln x = ∞.
14
Afgeleiden:
d
exp(x) = exp(x).
dx
1
d
ln x = .
dx
x
Het gevolg is dat ook andere afgeleiden bepaald kunnen worden.
Voor a > 0 en x ∈ R geldt
ax = ex ln a = exp(x ln a).
Er volgt dus
d x
a = ex ln a ln a = ax ln a.
dx
Evenzo, omdat a log x =
ln x
ln a ,
geldt
1
d a
.
log x =
dx
x ln a
15
Groei eigenschappen van exp en ln:
Voor a > 0 geldt
(i)
xa
limx→∞ ex
(ii) limx→∞
ln x
xa
= 0,
= 0,
(iii) limx→−∞ |x|a ex = 0,
(iv) limx↓0 xa ln x = 0.
Vuistregel:
• Een e-macht is sterker dan een macht van x,
• Een macht van x is sterker dan een logaritme.
16
Het bewijs van de groei-eigenschappen van exp en ln maakt gebruik van de
volgende
Stelling: Voor x > 0 geldt:
ln x ≤ x − 1.
Bewijs: Gebruik de middelwaardestelling.
17