Spanning in een elektrische kring

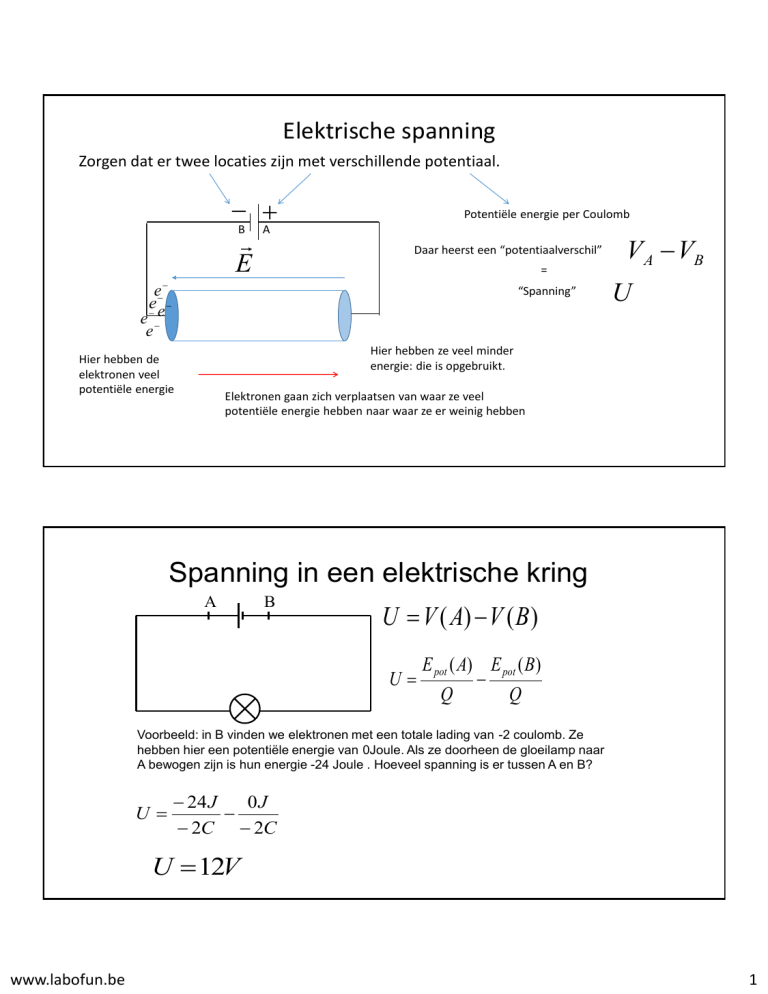
Elektrische spanning
Zorgen dat er twee locaties zijn met verschillende potentiaal.
 
B A

E
Potentiële energie per Coulomb
Daar heerst een “potentiaalverschil”
=
e
e e 
e
e
“Spanning”
VA  VB
U
Hier hebben ze veel minder
energie: die is opgebruikt.
Hier hebben de
elektronen veel
potentiële energie
Elektronen gaan zich verplaatsen van waar ze veel
potentiële energie hebben naar waar ze er weinig hebben
Spanning in een elektrische kring
A
B
U  V ( A)  V ( B)
U
E pot ( A) E pot ( B)

Q
Q
Voorbeeld: in B vinden we elektronen met een totale lading van -2 coulomb. Ze
hebben hier een potentiële energie van 0Joule. Als ze doorheen de gloeilamp naar
A bewogen zijn is hun energie -24 Joule . Hoeveel spanning is er tussen A en B?
U
 24 J
0J

 2C  2C
U  12V
www.labofun.be
1
Elektrische stroom

E
Het bewegen van ladingen.



e
ee
ee 
De elektrische stroomsterkte geeft weer hoeveel lading er per tijdseenheid doorheen een bepaalde doorsnede van een
geleider gaat.
I
Q
t
Elektrische stroomsterkte
Grootheid:
Elektrische stroomsterkte
Symbool:
I
Eenheid:
Ampère
Symbool van de eenheid:
A
De coulomb is de ladingshoeveelheid die gedurende 1s door de sectie van
een geleider gaat waarin een stroom van 1A vloeit.
1A  1
www.labofun.be
C
s
2
Conventionele stroomzin
A
B
I
Conventionele stroomzin: van + naar –
(omgekeerd van e- stroom)
Gelijkspanning in de tijd: wijzigt niet.
Wisselspanning in de tijd: sinusvorm.
U
U
t
t
Ladingscapaciteit van een batterij
Q  I .t
Grootheid:
Hoeveelheid lading
Symbool:
Q
Eenheid:
Ampèreseconde
Ampère-uur
Milliampère-uur
Symbool van de eenheid:
A.s (=1C)
A.h (=3600A.s=3600 C)
mA.h (3,6 C)
Qmax  I .t max
Bron: Soerfm
ladingscapaciteit
www.labofun.be
3
Meten van stroomsterkte
Stroom meten we met: Ampèremeter 
A
Kleine stromen: tot 200/250mA
Grote stromen
Positieve pool (rood);
voor stromen vanaf
200/250mA tot 10A
Positieve pool (rood);
voor stromen tot
200/250mA
Een Ampèremeter schakelen we in serie met het toestel
of de keten waardoor we de stroomsterkte willen meten.
Negatieve pool
Model op atomaire schaal

E

e v
V  l. A
Aantal vrije e- in ons
volume V
Aantal vrije e- per volumeeenheid = ladingsdichtheid
N  n.V
A
I
N  n.l. A
l
Totale lading in ons volume
Q  N .(e)
Elementaire lading
Q  n.l. A. e 
Q  n.v.t. A. e 
I
www.labofun.be
n.v.t. A.  e
t
v
l
t
I
Q
t
I  n.v. A.e
4
Driftsnelheid  snelheid van een elektron
I  n.v. A.e
e


v
A
I
Bereken de driftsnelheid in een koperen geleider van 1,00mm
doorsnede, waar een stroom van 4,0 A loopt. De
ladingsdichtheid voor koper is 8,5.1028 elektronen/m³
Geg : I  4,0 A; n  8,5.10 28 ; d  1,00.10 3 m
Gev : v ?


Opl : A   .r 2   . 0,5.10 3 m  7,85.10 7 m 2
I  n.v. A.e
v
4,0 I
1
8,5.10
.7,85.10 7 m 2 .1,60.10 19 C
3
m
28
www.labofun.be
v
2
I
n. A.e
v  3,8.10  4
m
mm
 0,38
s
s
velektron  1570
km
s
5