uitwerkingen

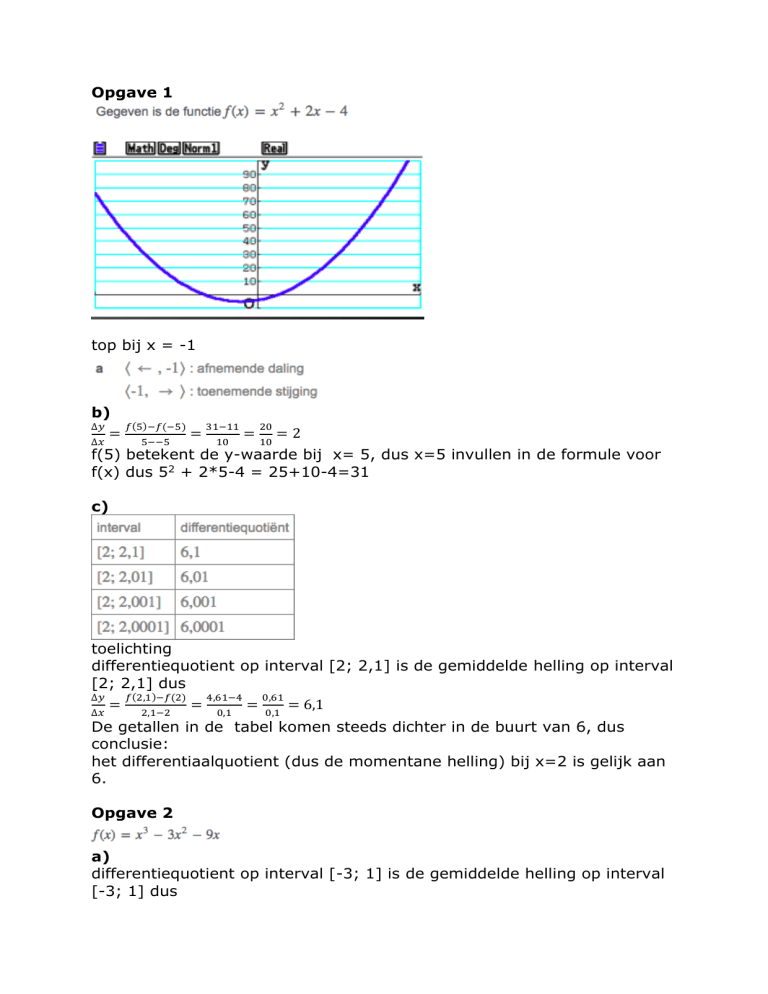
Opgave 1
top bij x = -1
b)
∆𝑦
𝑓(5)−𝑓(−5)
31−11
20
= 5−−5 = 10 = 10 = 2
∆𝑥
f(5) betekent de y-waarde bij x= 5, dus x=5 invullen in de formule voor
f(x) dus 52 + 2*5-4 = 25+10-4=31
c)
toelichting
differentiequotient op interval [2; 2,1] is de gemiddelde helling op interval
[2; 2,1] dus
∆𝑦
𝑓(2,1)−𝑓(2)
4,61−4
0,61
= 2,1−2 = 0,1 = 0,1 = 6,1
∆𝑥
De getallen in de tabel komen steeds dichter in de buurt van 6, dus
conclusie:
het differentiaalquotient (dus de momentane helling) bij x=2 is gelijk aan
6.
Opgave 2
a)
differentiequotient op interval [-3; 1] is de gemiddelde helling op interval
[-3; 1] dus
∆𝑦
∆𝑥
=
𝑓(1)−𝑓(−3)
1—3
=
−11—27
4
=
16
4
=4
b)
differentiequotient = 0 als 2 punten op gelijke hoogte liggen
c)
y = ax+b
raaklijn aan x = 1, en y = f(1) = 1-3-9= -11, dus het raakpunt = (1,-11)
de helling van de raaklijn = de helling van de grafiek in x=1 (want de
raaklijn heeft in x=1 dezelfde helling als de grafiek in x=1).
De helling kan je uitrekenen met je GRM
dus y = -12x+b
raakpunt (1,-11) invullen
-11 = -12*1 + b
-11 = -12 + b
b=1
Dus formule van de raaklijn y = -12x+1
d)
Voor de hellinggrafiek kijk je eerst naar de toppen.
De grafiek van f(x) heeft 2 toppen, bij x = -1 en x=3. Daar snijdt de
hellingsgrafiek dus de x-as.
Verder zie je
f(x) is dalend tussen x=-1 en x=3, dus daar is de hellingsgrafiek onder de
x-as, elders is de hellingsgrafiek boven de x-as.
Schets van hellingsgrafiek:
e)
extremen zijn maximum en minimum, daar is de helling altijd 0.
De nulpunten van de hellingsfunctie geven dus aan waar je extremen zijn.
Bij x = -1 en x=3
De bijbehorende y-waarden vind je door x=-1 en x=3 in te vullen in f(x)
Dus f(-1) = 5 en f(3) = -27
Dus coördinaten van het minimum van f(x)  (-1, 5)
En coördinaten van het maximum van f(x)  (3, -27)
Opgave 3
a)
t = 10 invullen dus h(10) = 100
b)
toelichting
toename bij t=1
bereken hiervoor de toename tussen t = 0 en t = 1 (want stapgrootte =
1)
dus h(0)= 0
h(1) = 60-5 = 55
dus toename = 55-0 = 55 en daarom zet je een streep van 55 omhoog
rest kan je zelf
c)
gemiddelde snelheid over de eerste 6 seconden= differentiequotient op
interval [0, 6] dus
∆𝑦
∆𝑥
=
𝑓(6)−𝑓(0)
6−0
=
180—0
6
=
180
6
= 30 𝑚𝑒𝑡𝑒𝑟/𝑠𝑒𝑐𝑜𝑛𝑑𝑒
d)
snelheid op t = 4 is het differentiaalquotient  met GRM
dus snelheid op t = 4 is 20 m/s
e)
x
Helling
0
60
2
40
4
20
6
0
8
-20
f)
y = ax+b (want het is een rechte lijn)
2 coordinaten aflezen en in tabel zetten
X
y
6
0
10
-40
a in formule = hellingsgetal =
∆𝑦
∆𝑥
=
−40
4
= −10
y = -10x+b
een van de coordinaten invullen, bijvoorbeeld (6,0)
0 = -10*6+b
0 = -60+b
b = 60
dus y = -10x+60
oftewel h’(t) = -10t + 60
moment van ontploffen t = 10, dus h’(10) = -100 + 60 = -40 m/s
opgave 4
a)
migratiesaldo = 3500, dus er zijn 3500 mensen bij gekomen
geboorte overschot = 2100
totale toename = 3500+2100 = 5600 mensen
b)
in 2014 is de toename van het aantal mensen voor het eerst negatief
c)
d)
Aantal inwoners
1-1-2010
1-1-2011
1-1-2012
1-1-2013
1-1-2014
1-1-2015
72600
78200
84700
88800
90000
88400
Toename/afname in
dat jaar
+5600
+6500
+4100
+1200
-1600
Opgave 5
a)
b)
In het vijfde jaar is de toename van het aantal kilogram vis het grootst ( 20000 kg).
Als de viskweker vijf jaar wacht is er 60000 kg vis en hij kan dan jaarlijks 20000 kg
vis vangen, precies de toename in dat vijfde jaar. Zo houdt hij steeds tussen de
40000 en de 60000 kg vis
Opgave 6




Grafiek 4 hoort bij model A want de helling is constant hetzelfde.
Grafiek 1 hoort bij model B want de helling neemt voortdurend af. (afnemend stijgend naar toenemend
dalend, dus de helling wordt alsmaar minder en minder)
Grafiek 3 hoort bij model C want de helling neemt eerst toe en dan af maar blijft positief.
Grafiek 2 hoort bij model D want de helling neemt eerst toe en dan af en wordt negatief. (want de
grafiek stijgt eerst, en daalt daarna