Parallax: wat is het en waarom zien we het niet?

Parallax: wat is het en waarom zien we het niet?
Voorlopig beelden we ons een wereld in zonder de zon en met een aarde die niet
draait. In die wereld staan alle sterren stil en zijn ze voortdurend zichtbaar,
zolang ze tenminste boven de horizon staan.
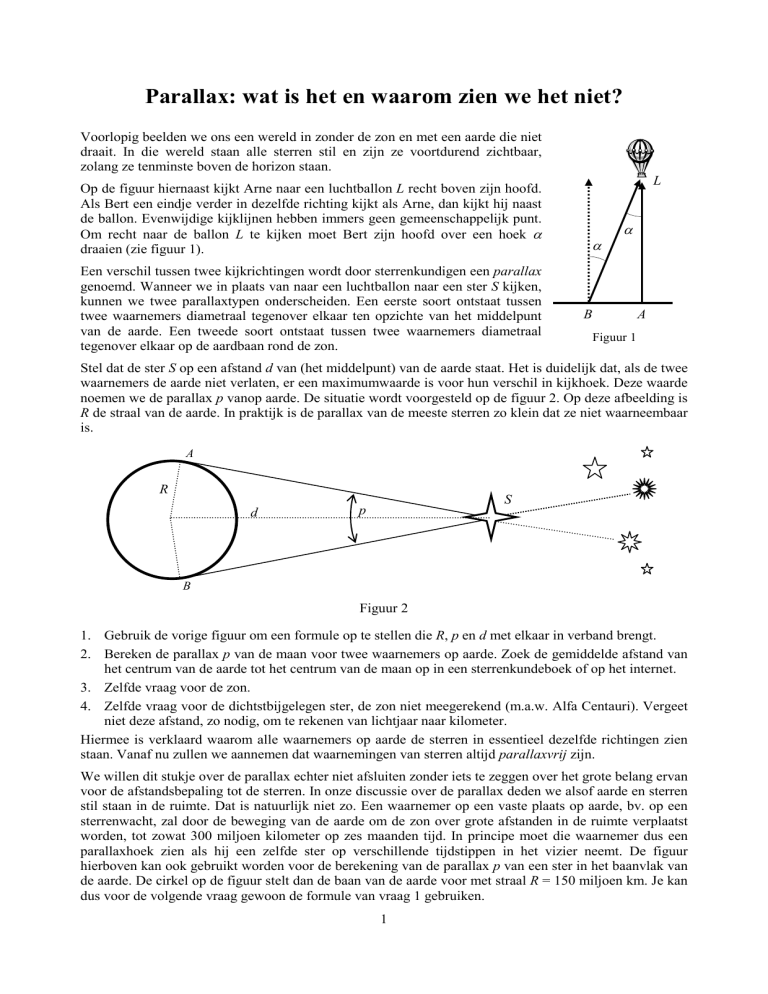
Op de figuur hiernaast kijkt Arne naar een luchtballon L recht boven zijn hoofd.
Als Bert een eindje verder in dezelfde richting kijkt als Arne, dan kijkt hij naast
de ballon. Evenwijdige kijklijnen hebben immers geen gemeenschappelijk punt.
Om recht naar de ballon L te kijken moet Bert zijn hoofd over een hoek α
draaien (zie figuur 1).
Een verschil tussen twee kijkrichtingen wordt door sterrenkundigen een parallax
genoemd. Wanneer we in plaats van naar een luchtballon naar een ster S kijken,
kunnen we twee parallaxtypen onderscheiden. Een eerste soort ontstaat tussen
twee waarnemers diametraal tegenover elkaar ten opzichte van het middelpunt
van de aarde. Een tweede soort ontstaat tussen twee waarnemers diametraal
tegenover elkaar op de aardbaan rond de zon.
L
α
α
A
B
Figuur 1
Stel dat de ster S op een afstand d van (het middelpunt) van de aarde staat. Het is duidelijk dat, als de twee
waarnemers de aarde niet verlaten, er een maximumwaarde is voor hun verschil in kijkhoek. Deze waarde
noemen we de parallax p vanop aarde. De situatie wordt voorgesteld op de figuur 2. Op deze afbeelding is
R de straal van de aarde. In praktijk is de parallax van de meeste sterren zo klein dat ze niet waarneembaar
is.
A
R
d
S
p
B
Figuur 2
1. Gebruik de vorige figuur om een formule op te stellen die R, p en d met elkaar in verband brengt.
2. Bereken de parallax p van de maan voor twee waarnemers op aarde. Zoek de gemiddelde afstand van
het centrum van de aarde tot het centrum van de maan op in een sterrenkundeboek of op het internet.
3. Zelfde vraag voor de zon.
4. Zelfde vraag voor de dichtstbijgelegen ster, de zon niet meegerekend (m.a.w. Alfa Centauri). Vergeet
niet deze afstand, zo nodig, om te rekenen van lichtjaar naar kilometer.
Hiermee is verklaard waarom alle waarnemers op aarde de sterren in essentieel dezelfde richtingen zien
staan. Vanaf nu zullen we aannemen dat waarnemingen van sterren altijd parallaxvrij zijn.
We willen dit stukje over de parallax echter niet afsluiten zonder iets te zeggen over het grote belang ervan
voor de afstandsbepaling tot de sterren. In onze discussie over de parallax deden we alsof aarde en sterren
stil staan in de ruimte. Dat is natuurlijk niet zo. Een waarnemer op een vaste plaats op aarde, bv. op een
sterrenwacht, zal door de beweging van de aarde om de zon over grote afstanden in de ruimte verplaatst
worden, tot zowat 300 miljoen kilometer op zes maanden tijd. In principe moet die waarnemer dus een
parallaxhoek zien als hij een zelfde ster op verschillende tijdstippen in het vizier neemt. De figuur
hierboven kan ook gebruikt worden voor de berekening van de parallax p van een ster in het baanvlak van
de aarde. De cirkel op de figuur stelt dan de baan van de aarde voor met straal R = 150 miljoen km. Je kan
dus voor de volgende vraag gewoon de formule van vraag 1 gebruiken.
1
5. Door in een tussentijd van zes maanden twee waarnemingen van de ster Alfa Centauri met elkaar te
vergelijken heeft men een parallax gemeten van 1,54''. Bereken hieruit de afstand van deze ster tot de
zon.
6. Om je deze kleine parallaxhoek te kunnen inbeelden geven we de volgende vergelijking. Arne en Bert
kijken naar een vlaggenmast. Ze staan 1 meter van elkaar, dwars op de kijkrichting gemeten. De
parallax die ze ondervinden bedraagt 1,54'' (vergelijkbaar met die van Alfa Centauri, maar daar staan
de waarnemers 300 miljoen kilometer van elkaar). Bereken de afstand tot de vlaggenmast.
Het is ondertussen duidelijk geworden dat parallaxhoeken slechts met de grootste moeite meetbaar zijn.
Het overgrote deel van de vaste sterren heeft geen waarneembare parallax, zelfs niet ten gevolge van de
draaiing van de aarde rond de zon. Alleen sterren die dichterbij staan dan de meeste van de
achtergrondsterren hebben een meetbare parallax. Twee waarnemers A en B die ver genoeg uit elkaar
staan, stellen bij zulke sterren vast dat ze een andere achtergrondster overdekken. Parallaxen van
voorgrondsterren worden bijgevolg praktisch waargenomen ten opzicht van achtergrondsterren (zie figuur
2).
Het heeft tot 1838 geduurd voor Bessel als eerste een parallaxhoek heeft gemeten (0,63'' voor ster 61 uit
het sterrenbeeld van de Zwaan). Niet alleen de meting zelf was een krachttoer, maar ook het uitpuzzelen
van welke sterren in aanmerking kwamen tussen de vele tienduizenden kandidaten.
Zoals je in vraag 5 hebt gedaan, kan je de afstand berekenen tot elke ster die een meetbare parallax
vertoont. Enkel van die sterren kan men de afstand met grote precisie bepalen. Afstanden bepalen tot
verder gelegen sterren is een mooi stukje detectivewerk, maar meer informatie hierover moet je elders
zoeken. Tegenwoordig meet men parallaxen volautomatisch met satellieten. Enkele jaren geleden bracht
de satelliet Hipparchos een revolutie in onze kennis van de sterren teweeg door van meer dan 100.000
sterren de parallax tot op 0,002 boogseconden nauwkeurig te meten. Een geplande opvolger FAME zal de
precisie opdrijven tot 50 miljoensten van een boogseconde, dit is de hoek waaronder je een haardikte ziet
op een afstand van enkele honderden kilometers.
2