Rekenen met letters

G22
Rekenen met letters
Op verkenning
a
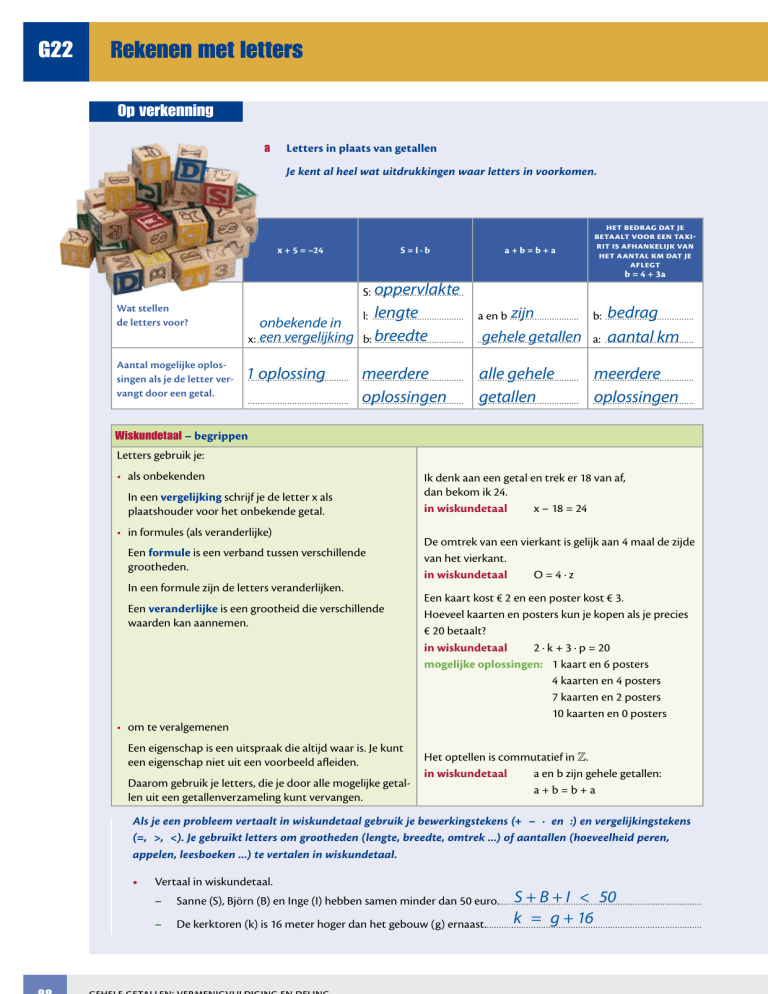
Letters in plaats van getallen
Je kent al heel wat uitdrukkingen waar letters in voorkomen.
x + 5 = –24
S=l·b
a+b=b+a
Het bedrag dat je
betaalt voor een taxirit is afhankelijk van
het aantal km dat je
aflegt
b = 4 + 3a
zijn
a en b ............................
bedrag . . . . . . . . .. . . .
b: .......................
S: oppervlakte
....................................
Wat stellen
de letters voor?
Aantal mogelijke oplossingen als je de letter vervangt door een getal.
l:
lengte
.....................................
onbekende in
x: .een
. . . . . . . . . .vergelijking
. . . . . . . . . . . . . . . . . . ........
b: breedte
....................................
gehele getallen
.........................................
a:
aantal km
....................... . . . . . . . . .. . . .
1. . . . .oplossing
alle gehele
meerdere . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . ........ meerdere
.........................................
.........................................
.............................
getallen
oplossingen
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ........ oplossingen
.........................................
.........................................
.............................
............
Wiskundetaal – begrippen
Letters gebruik je:
t als onbekenden
In een vergelijking schrijf je de letter x als
plaatshouder voor het onbekende getal.
t in formules (als veranderlijke)
Een formule is een verband tussen verschillende
grootheden.
In een formule zijn de letters veranderlijken.
Een veranderlijke is een grootheid die verschillende
waarden kan aannemen.
t om te veralgemenen
Een eigenschap is een uitspraak die altijd waar is. Je kunt
een eigenschap niet uit een voorbeeld afleiden.
Daarom gebruik je letters, die je door alle mogelijke getallen uit een getallenverzameling kunt vervangen.
Ik denk aan een getal en trek er 18 van af,
dan bekom ik 24.
in wiskundetaal
x – 18 = 24
De omtrek van een vierkant is gelijk aan 4 maal de zijde
van het vierkant.
in wiskundetaal
O=4·z
Een kaart kost € 2 en een poster kost € 3.
Hoeveel kaarten en posters kun je kopen als je precies
€ 20 betaalt?
in wiskundetaal
2 · k + 3 · p = 20
mogelijke oplossingen: 1 kaart en 6 posters
4 kaarten en 4 posters
7 kaarten en 2 posters
10 kaarten en 0 posters
Het optellen is commutatief in ℤ.
in wiskundetaal
a en b zijn gehele getallen:
a+b=b+a
Als je een probleem vertaalt in wiskundetaal gebruik je bewerkingstekens (+ – · en :) en vergelijkingstekens
(=, >, <). Je gebruikt letters om grootheden (lengte, breedte, omtrek ...) of aantallen (hoeveelheid peren,
appelen, leesboeken ...) te vertalen in wiskundetaal.
t
Vertaal in wiskundetaal.
–
–
S + B + I < 50
. . . . . . . . .. . . . . . .
Sanne (S), Björn (B) en Inge (I) hebben samen minder dan 50 euro...................................................................
k = g + 16
De kerktoren (k) is 16 meter hoger dan het gebouw (g) ernaast.........................................................................
...............
Wiskundetaal – begrippen
b
Een lettervorm is een uitdrukking waarin letters en getallen
voorkomen.
3a + 4b
3c
2k + 3p = 20
Een lettervorm (die een product voorstelt) bestaat uit een
cijfergedeelte (coëfficiënt) en een lettergedeelte.
4·z
Belangrijke afspraken:
t Schrijf eerst het cijfergedeelte en daarna het lettergedeelte.
t Als het cijfergedeelte 1 is, laat je 1 weg.
t Laat het vermenigvuldigingsteken weg als er geen verwarring
mogelijk is.
z·4
4·z
1·a
a
4·z
4z
b·h
bh
7 · 5 blijft 7 · 5
cijfergedeelte (coëfficiënt)
lettergedeelte
Lettervormen optellen
t Bereken de omtrek van deze figuren met een optelling.
t Bereken de omtrek van deze figuren met een vermenigvuldiging.
11
5
5
11
5
a
11
11
a
11
a
5
5
11
5
5+5+5+5+5+5
= 30
6·5
= 30
11
a
a
11
11
+ 11 + 11 + 11 + 11 + 11 + 11 + 11
....................................................................
a........................................................
+ a + a + a + a ............
88
= ................................................................
5a
........................................................ . . . . . . . . . . . .
8....................................................................
· 11
88
= ................................................................
Zeth en Elle brengen elk frisdrank en chips mee naar het klasfeestje. Zeth heeft 6 zakjes (z) en 11 flesjes (f) bij,
Elle 7 zakjes en 7 flesjes. Hoeveel zakjes chips en flesjes frisdrank hebben ze samen?
t Schrijf in wiskundetaal.
(6z + . . . . .11f
. . . . . . . . . . . ) + (. . . . . .7z
. . . . . . . . . . + . . . . . .7f
. . . . . . . . . .)
11f + 7z + 7f
6z + 7z + 11f + 7f = 13z + 18f . . . . . . . . . . . . . . .
= ..............................................................................................
Je kunt geen flesjes en
...................................................................................................
. . . . . . . . .. . . . . . .
zakjes samentellen. (= niet gelijksoortig)
...................................................................................................
. . . . . . . . .. . . . . . .
= 6z +
t
Je kunt termen met z niet optellen bij
termen met f. Verklaar waarom.
................................................................................. . . . . . . . . . . . . . . .
Rekenregel – lettervormen optellen
Je kunt alleen termen bij elkaar optellen die hetzelfde lettergedeelte hebben. 5a + a = 6a
2a + b = 2a + b
t Tel de coëfficiënten bij elkaar op.
5d + 8 = 5d + 8
t Behoud het lettergedeelte.
10b – 15b = –5b
3a + 5b + 10a – 7b = 13a – 2b
CONTROLE 34 Werk zo ver mogelijk uit.
4a + 3b + 6a
7a – 5 + 4b + 2
=
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..............................
10a + 3b
=
7a
+ 4b – 3
..........................................................................................
. . . . . . . . .. . . . .
=
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .............................
=
.......................................................................................... . . . . . . . . .. . . . .
(2a – 8b + 7b) + 4a
=
=
2a – 8b + 7b + 4a
.6a
........–
. . . . .b
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .............................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .............................
(13a – 8) + (9b – 4)
13a
– 8 + 9b – 4
..........................................................................................
. . . . . . . . .. . . . .
+ 9b – 12
= 13a
..........................................................................................
. . . . . . . . .. . . . . .
=
G22
Rekenen met letters (vervolg)
c
Lettervormen vermenigvuldigen met een getal
t Bereken de totale omtrek van deze gelijkzijdige driehoeken.
a
a
a
3 · a = 3a
t
a
a a
a
a
a
a
a
a
2 · 3a = 2 · 3 · a
= (2 · 3) · a
= .6
.... · a
6a
= .....
a
a
a
a
a
a
3........................................
· 3a = 3 · 3 ·. .a
=
(3 · 3) · a . .
........................................
=
9·a
........................................
..
=
9a
........................................
..
Welke eigenschap pas je toe om de cijfergedeelten (coëfficiënten) met elkaar te vermenigvuldigen?
Het vermenigvuldigen is associatief in nj.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ...................................................................................................................................... . . . . . . . . .. . . . . . .
De flessen frisdrank (f) in een warenhuis zitten per zes in een pak (p). In de drankenhoek staan nog 18 pakken
met flessen gestapeld. Hoeveel flessen zijn dat in totaal?
t
Schrijf in wiskundetaal.
. . . . . . · f)
18p = 18 · (. .6
= 18 · . . .6
..... · f
= .108
. . . . . . . . . . .·. .f. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
= .108f
................................................................
Rekenregel – een lettervorm die een product voorstelt vermenigvuldigen met een getal
3 . 4a = 12a
t Vermenigvuldig het getal met de coëfficiënt.
10 . 5b = 50b
t Behoud het lettergedeelte.
7 . 6cd = 42cd
CONTROLE 35 Reken uit.
2a · 9 = .18a
........................
–6 · 4b = .–24b
........................
d
8a · (–3) = .–24a
........................
Lettervormen vermenigvuldigen
3b
b
a
t
–5b · (–1) = .5b
........................
ab
ab
ab
2a
Bereken de oppervlakte.
a·b
ab
.=
. . . . . ..........................................................
. . . . . . ..........................................................
t
Teken een rechthoek met twee keer
breedte a en drie keer lengte b.
t
Bereken de oppervlakte van
de grote rechthoek.
ab
ab
ab
2a · 3b = 6ab
. . . . . . ..........................................................
t
Hoe vaak past de gegeven rechthoek
in de grote rechthoek? . . . .6
. . . . . . keer
Rekenregel – lettervormen vermenigvuldigen
t Vermenigvuldig de coëfficiënten.
t Vermenigvuldig de lettergedeelten.
3a · 2b = 6ab
5a · 2a = 10aa
3a · 2b · 5c = 30abc
3a · (–2b) · 5c = –30abc
Oefeningen
19 Reken uit.
a
2T + 5T = 7T
............
c
2 · 3T =
b
5E – 11E = –6E
............
d
–3 · 9E =
6T
–27E
..........
..........
e
2T + 2E + 8T + 3E =
f
5H + 10E + 9H – 15 E =
d
4d – d + 3d =
20 Reken zo ver mogelijk uit.
a
2a + 3a =
b
4b + b =
c
3c – 2c =
5a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
5b
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
.1c
. . . . . . . . . .=
. . . . . . . .c
. . . . . . . . . . . . . . . . . . . . . . .........................
e
f
10T + 5E
14H – .5E
....................
. . . . . . . .. . . . . .
.................... . . . . . . . . .. . . . . .
6d
2e
–2e + 4e = .............................................
...............
0
–5f + 5f = ...............................................
...............
........................................ . . . . . . . . . . . . . .
5a + 5b
5 · (a + b) =
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
b
3 · (a + b) =
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
c
10 · (a + b + c) =
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
d
12 · (x + y + 2) =
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .........................
22 t
t
MEER?
279
WEER?
280
MEER?
281
WEER?
282
21 De letters stellen willekeurige gehele getallen voor. Werk de haakjes weg.
a
WEER?
278
MEER?
283
3a + 3b
10a + 10b + 10c
12x + 12y + 12 · 2 = 12x + 12y + 24
Werk eerst de haakjes weg.
Werk dan uit zo ver je kunt.
a
(5a – 3b) – (a – b + c) =
b
3a + (2a – b + c) =
c
– (a – b) + (c – d) =
d
(a + 3c) – (a – 2c + d) =
5a – 3b – a + b – c = 4a – 2b – c
3a + 2a – b + c = 5a – b + c
.............................................................................................................
...............
–a + b + c – d
.............................................................................................................
...............
a + 3c – a + 2c – d = 5c – d
.............................................................................................................
...............
............................................................................................................. . . . . . . . . . . . . . . .
WEER?
284
285
MEER?
286
287
23 Bereken de omtrek van elke veelhoek.
x
h
y
g
g
y
x
v
x
y
y
x
h
2g
. . . . . . . . .+
. . . . . .2h
. . . . . . . . . . .. . . . . . . . . . . . . .
m
p
n
4x
. . . . . . . .+
. . . . . .8y
. . . . . . . . ..................
8m + 8n
........................................
6p
+ 6v . . . . . . . . . . .
.............................
Wat moet je kunnen?
τ twee lettervormen optellen
τ twee lettervormen vermenigvuldigen
τ een getal en een lettervorm met elkaar
vermenigvuldigen
WEER?
293
294
MEER?
295
296