Samenvatting Kansberekening en statistiek: Direct en

lOMoARcPSD
Soorten kansverdeling
Discrete verdeling
Bernoulli verdeling:
Wordt gebruikt om een experiment te schetsen met slechts twee mogelijke uitkomsten, vaak
beschreven als ‘succes’ of ‘mislukking’.
Vb.: Je moet kiezen uit 2 dozen, in 1 van de dozen zit een prijs en de andere doos is leeg. De kans dat
de prijs in doos 1 zit is p en de kans dat de prijs in doos 2 zit is 1-p waarbij 0<p<1.
Binomiale verdeling:
Verdeling van het aantal successen X in een reeks van n onafhankelijke alternatieven allen met
succeskans p. In het geval n = 1 komt de binomiale verdeling overeen met de Bernoulli verdeling.
Vb.: We gooien 4 keer met een dobbelsteen. We kunnen 0, 1, 2, 3 of 4 keer een 6 gooien. Het aantal
keren dat we 6 gooien, X, is Bin(4,1/6)-verdeeld. De kans dat we van de 4 worpen 1 keer een 6
gooien is: (n=4, p=1/6 en k=1 (je wilt 1 keer een 6 gooien))
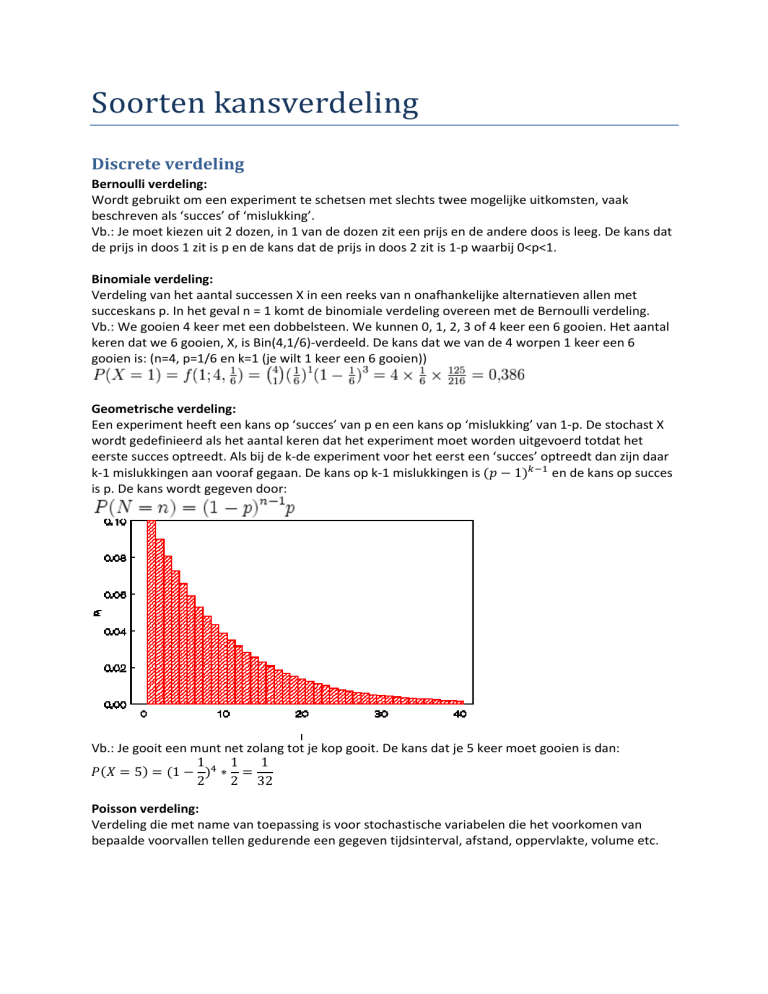
Geometrische verdeling:
Een experiment heeft een kans op ‘succes’ van p en een kans op ‘mislukking’ van 1-p. De stochast X
wordt gedefinieerd als het aantal keren dat het experiment moet worden uitgevoerd totdat het
eerste succes optreedt. Als bij de k-de experiment voor het eerst een ‘succes’ optreedt dan zijn daar
en de kans op succes
k-1 mislukkingen aan vooraf gegaan. De kans op k-1 mislukkingen is
1
is p. De kans wordt gegeven door:
Vb.: Je gooit een munt net zolang tot je kop gooit. De kans dat je 5 keer moet gooien is dan:
1
1
1
∗
5
1
2 32
2
Poisson verdeling:
Verdeling die met name van toepassing is voor stochastische variabelen die het voorkomen van
bepaalde voorvallen tellen gedurende een gegeven tijdsinterval, afstand, oppervlakte, volume etc.
lOMoARcPSD
Het linker plaatje geeft de kansdichtheid en het rechter plaatje de verdelingsfunctie.
k kan alleen gehele waarden aannemen. Voor de kans geldt:
Vb.: Als er bijvoorbeeld 1 voorval elke 2 minuten wordt verwacht en het tijdsinterval is 10 minuten,
dan zou een poissonverdeling met λ=5 moeten worden gebruikt.
6
!
0.0538
Continue verdeling
Cauchy verdeling:
De verdeling van een bepaalde klasse van stochastische variabelen. De cauchy verdeling is een
symmetrische verdeling met zwaardere staarten dan de normale verdeling.
De blauwe kromme geeft de dichtheidsfunctie van de standaard Cauchy-verdeling weer. De rode
kromme is de verdelingsfunctie, de integraal van de dichtheidsfunctie.
Exponentiële verdeling:
De exponentiële verdeling wordt vaak gebruikt voor het modelleren van de tijd tussen twee
gebeurtenissen die met een constante gemiddelde snelheid voorkomen. Het is een specifiek geval
van de gamma verdeling.
lOMoARcPSD
Hierbij geeft het linker plaatje de kansdichtheid en het rechterplaatje de verdelingsfunctie.
De kansdichtheid f van een exponentiële verdeling wordt gegeven door:
Waar λ>0 de parameter van de verdeling is, die vaak een snelheidsparameter of
intensiteitsparameter is. De verdeling wordt gedragen door het interval [0,∞).
De exponentiële verdeling heeft als merkwaardig eigenschap geheugenloosheid. Als X een
levensduur is die exponentieel verdeeld is, worden de overlevingskansen voor x>0 gegeven door:
.
Vb.: De tijd die zal verstrijken tot de eerstvolgende telefoon oproep, wanneer er gemiddeld λ oproepen
per tijdseenheid zijn.
Gamma verdeling:
Deze verdeling wordt vaak gebruikt wanneer er meerdere, onderling onafhankelijke experimenten
met een exponentiële verdeling in het spel zijn. De gamma verdeling heeft twee parameters. Als X
een gamma (1,θ)-verdeling heeft, dan heeft X een exponentiële verdeling met parameter λ=1/θ.
Hierbij geeft het linker plaatje de kansdichtheid en het rechter plaatje de verdelingsfunctie.
Vb.: Stel dat de wachttijd in minuten op de bus bij een halte een exponentiële verdeling met
parameter λ=10 heeft, dan is de wachttijd op de vijfde bus verdeeld volgens de gamma (5,1/10)verdeling.
Normale verdeling:
Een normale verdeling heeft een verwachtingswaarde van µ en een standaardafwijking σ. Het gaat
dan om verschijnselen waarvan de verdeling symmetrisch geconcentreerd is rond een centrale
waarde en afwijkingen van deze centrale waarde steeds onwaarschijnlijker worden naarmate de
afwijking groter is. Soms is het verschijnsel de optelsom van een groot aantal effecten die elkaar niet
beïnvloeden. De N(0,1)-verdeling wordt ook wel een standaardnormale verdeling genoemd.
lOMoARcPSD
Vb.: Met behulp van de normale verdeling kan men een schatting maken van de gemiddelde lengte
van Nederlandse mannen en de standaardafwijking van de verdeling door een steekproef van
honderden mannen te nemen en daarvan de lengte te meten.
Pareto verdeling:
Deze verdeling werd oorspronkelijk gebruikt als model voor de verdeling van rijkdom. Het
paretoprincipe zegt dat 20% van de bevolking 80% van de rijkdom bezit. De pareto-verdeling is
geschikt om zo’n situatie te beschrijven. Andere situaties kunnen ook met de pareto-verdeling
worden beschreven. Zoals de frequentie van woorden in een tekst (slechts een klein aantal woorden
vormt het grootste deel van de tekst).
Uniforme verdeling:
Een verdeling op een interval met een constante kansdichtheid. Dit houdt in dat er geen voorkeur is
voor enige waarde uit dat interval. Voor de uniforme verdeling op het interval (a,b) wordt de
kansdichtheid f dus gegeven door:
Het linker plaatje geeft de kansdichtheid weer en het rechterplaatje de verdelingsfunctie.
Vb.: De gemiddelde hoeveelheid bier die er op een drukke avond doorheen gaat in een populaire
kroeg is uniform verdeeld met een minimum van 200 liter (= a) en een maximum van 500 liter (= b) .
De kans dat er op een avond tussen de 250 (= x1) en 300 (= x2) liter bier doorheen gaat wordt als volgt
berekend: