Par 1. 1a. De uitslag bij beide elektroscopen verdwijnt, omdat de

Par 1.
1a.
1b.
2a.
2b.
De uitslag bij beide elektroscopen verdwijnt, omdat de ladingen elkaar opheffen.
De elektronen van de negatief geladen elektroscoop die te veel zijn, vloeien naar de positief geladen elektroscoop
waar te weinig elektronen zijn. Beide elektroscopen zijn na afloop neutraal.
De elektronen zijn van haar vinger naar de elektriseermachine gegaan.
Bij het lichtnet is de spanning voortdurend aanwezig en kan er continu een stroom lopen. Dat is gevaarlijker, omdat
het gevaar langer blijft bestaan.
Par 2.
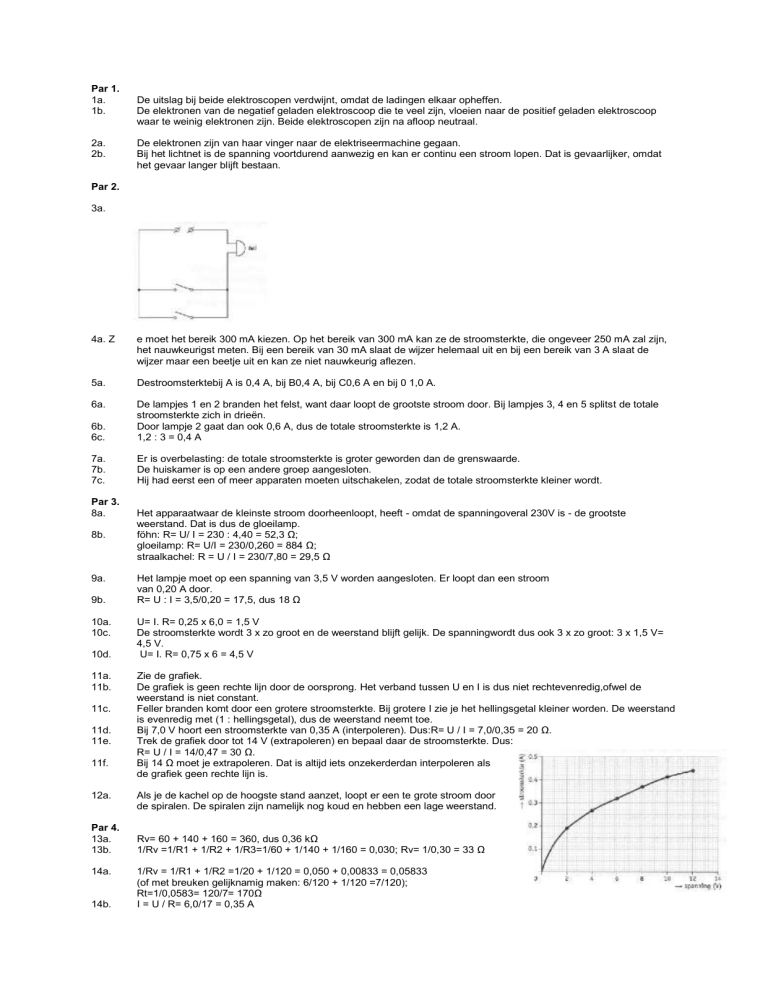
3a.
4a. Z
e moet het bereik 300 mA kiezen. Op het bereik van 300 mA kan ze de stroomsterkte, die ongeveer 250 mA zal zijn,
het nauwkeurigst meten. Bij een bereik van 30 mA slaat de wijzer helemaal uit en bij een bereik van 3 A slaat de
wijzer maar een beetje uit en kan ze niet nauwkeurig aflezen.
5a.
Destroomsterktebij A is 0,4 A, bij B0,4 A, bij C0,6 A en bij 0 1,0 A.
6a.
6b.
6c.
De lampjes 1 en 2 branden het felst, want daar loopt de grootste stroom door. Bij lampjes 3, 4 en 5 splitst de totale
stroomsterkte zich in drieën.
Door lampje 2 gaat dan ook 0,6 A, dus de totale stroomsterkte is 1,2 A.
1,2 : 3 = 0,4 A
7a.
7b.
7c.
Er is overbelasting: de totale stroomsterkte is groter geworden dan de grenswaarde.
De huiskamer is op een andere groep aangesloten.
Hij had eerst een of meer apparaten moeten uitschakelen, zodat de totale stroomsterkte kleiner wordt.
Par 3.
8a.
8b.
9a.
9b.
10a.
10c.
10d.
11a.
11b.
11c.
11d.
11e.
11f.
12a.
Par 4.
13a.
13b.
14a.
14b.
Het apparaatwaar de kleinste stroom doorheenloopt, heeft - omdat de spanningoveral 230V is - de grootste
weerstand. Dat is dus de gloeilamp.
föhn: R= U/ I = 230 : 4,40 = 52,3 Ω;
gloeilamp: R= U/I = 230/0,260 = 884 Ω;
straalkachel: R = U / I = 230/7,80 = 29,5 Ω
Het lampje moet op een spanning van 3,5 V worden aangesloten. Er loopt dan een stroom
van 0,20 A door.
R= U : I = 3,5/0,20 = 17,5, dus 18 Ω
U= I. R= 0,25 x 6,0 = 1,5 V
De stroomsterkte wordt 3 x zo groot en de weerstand blijft gelijk. De spanningwordt dus ook 3 x zo groot: 3 x 1,5 V=
4,5 V.
U= I. R= 0,75 x 6 = 4,5 V
Zie de grafiek.
De grafiek is geen rechte lijn door de oorsprong. Het verband tussen U en I is dus niet rechtevenredig,ofwel de
weerstand is niet constant.
Feller branden komt door een grotere stroomsterkte. Bij grotere I zie je het hellingsgetal kleiner worden. De weerstand
is evenredig met (1 : hellingsgetal), dus de weerstand neemt toe.
Bij 7,0 V hoort een stroomsterkte van 0,35 A (interpoleren). Dus:R= U / I = 7,0/0,35 = 20 Ω.
Trek de grafiek door tot 14 V (extrapoleren) en bepaal daar de stroomsterkte. Dus:
R= U / I = 14/0,47 = 30 Ω.
Bij 14 Ω moet je extrapoleren. Dat is altijd iets onzekerderdan interpoleren als
de grafiek geen rechte lijn is.
Als je de kachel op de hoogste stand aanzet, loopt er een te grote stroom door
de spiralen. De spiralen zijn namelijk nog koud en hebben een lage weerstand.
Rv= 60 + 140 + 160 = 360, dus 0,36 kΩ
1/Rv =1/R1 + 1/R2 + 1/R3=1/60 + 1/140 + 1/160 = 0,030; Rv= 1/0,30 = 33 Ω
1/Rv = 1/R1 + 1/R2 =1/20 + 1/120 = 0,050 + 0,00833 = 0,05833
(of met breuken gelijknamig maken: 6/120 + 1/120 =7/120);
Rt=1/0,0583= 120/7= 170Ω
I = U / R= 6,0/17 = 0,35 A
15a.
15b.
15c.
In stand 3 is de totale weerstand het kleinst en de stroomsterkte het grootst. Hier staan
de drie draden namelijk parallel.
1/Rv = 1/R1 + 1/R2 + R3= 1/100 + 1/100 + 1/100 = 3/100; Rv= 100/3 = 33,3 Ω
I= U/R= 230/33,3 = 6,91 A
16a.
16b.
16c.
Zie figuur 10.
in serie
I= 230/(1 000 000 + 1000) = 230/1 001 000 = 0,000 23, dus 0,23
mA
17a.
17b.
R=U/I = 10/0,30 = 33,3, dus 33 Ω
Over alle lampjes staat 10 V spanning, dus er zijn blijkbaar 23
lampjes.
Rt = 23 x 33,3 of Rt= 230/0,30; in beide gevallen levert dat 0,77
kΩ.
De stroomsterkte wordt groter. Er is een lampje minder,dus de
totale weerstand is kleiner geworden.
17c.
17d.
18a.
Par 5.
19a.
19b.
19c.
1/Ry = 1/R1 + 1/R2 + 1/R3 ; 1/15 =1/60 + 1/40 + 1/X;
1/X =1/15 - 1/40 - 1/60 = 8/120 - 3/120 - 2/120 =3/120 = 0,025;
X= 120/3= 1/0,025= 40Ω
De gloeilamp in de bureaulamp,want meer licht betekent meestal meervermogen.
De gloeilamp in de bureaulamp,want sterker licht is het gevolg van een grotere stroomsterkte.
De gloeilamp in het spotje, want daar gaat bij dezelfde spanning minder stroom doorheen.
20a.
Reken eerst de totale stroomsterkte uit: totale vermogen=1200 + 2200 + 125 = 3525 W,
dus I = P/ U=3525/230 = 15,3 A. De zekering zal dus niet doorsmelten
21a.
Totale vermogen =(2 x 60) + (3 x 5) =135 W= 0,135 kW;tijd: 1,75 uur; dus E = 0,135 x 1,75 = 0,24 kWh
22a.
Aantal kWh= 26,88; aantal uur = 4 x 7 x 24 = 672; dus P= 26,88/672 = 0,040 kW= 40W
23a.
P= U . I = 1500x 300=450 kW;E=P . t = 450 x 0,5 = 225 kWh. Dit kost: 225 x € 0,20 = € 45.
24a.
24b.
24c.
E = 0,000 3 x 8 = 0,002 4 kWh
0,0024 x € 0,20= € 0,00048
De energie uit batterijen is veel duurder dan die uit het stopcontact.
25a.
25b.
25c.
Tussen 19.55 uuren21.00 uur;P= 0,73kW
Om ongeveer 23.00 uur; P = 0,58 kW
Door de tijd een uur 'op te schuiven’ is het ’s avonds langer licht. De verlichting kan dan ook een uur later aan.
26a.
R= U/ I en U= P / I. Als je deze twee formules combineert, krijg je de gevraagde formule.
R = P / I / I = P / I2
Par 6.
27a.
28a.
De weerstand hangt af van de temperatuur,van de lengte van de draad,van de doorsnede van
de draad en van het materiaal waarvan de draad is gemaakt.
Een bronzendraad met een lengte van 1 men een doorsnede van 1 mm2 heeft een weerstand
van 0,30 Ω.
29a.
29b.
29c.
0,50/0,14 = 3,57, dus 3,6 Ω
De doorsnede A = π × r2 met r = straal = halve diameter= 0,10 mm, dus A = 0,031 mm2;
ρ= R×A /l= 3,57 x 0,031/1 = 0,11 Ω × mm2/m
Volgens de tabel in het handboek is de soortelijke weerstand van ijzer 0,105, dus de meting is behoorlijk nauwkeurig.
30a.
A = ρ × l / R= 0,45 × 4,0/2,0 = 0,90 mm2; A = π r2, dus (= √(A / π) = 0,54;
dus de diameter d = 2 × 0,54 = 1,1 mm
31a.
R= ρ × I/A = 0,027 × 6,0/2,0 = 0,027 × 3,0 = 0,081 0; I = U / R= 0,45/0,081 = 7,4 A
32a.
R= 230/0,260 = 885; 1= R×A / ρ = 885 x 0;000 50/0,880 = 0,50 m