Raf: 0032-486287070

H19. Basiskennis meetkunde.
Basiskennis meetkunde geeft met name een overzicht van de stof
die noodzakelijke basiskennis is voor H20. Bewijzen meetkunde.
§19.1 Vierhoeken.
De som van de hoeken van een vierkant.
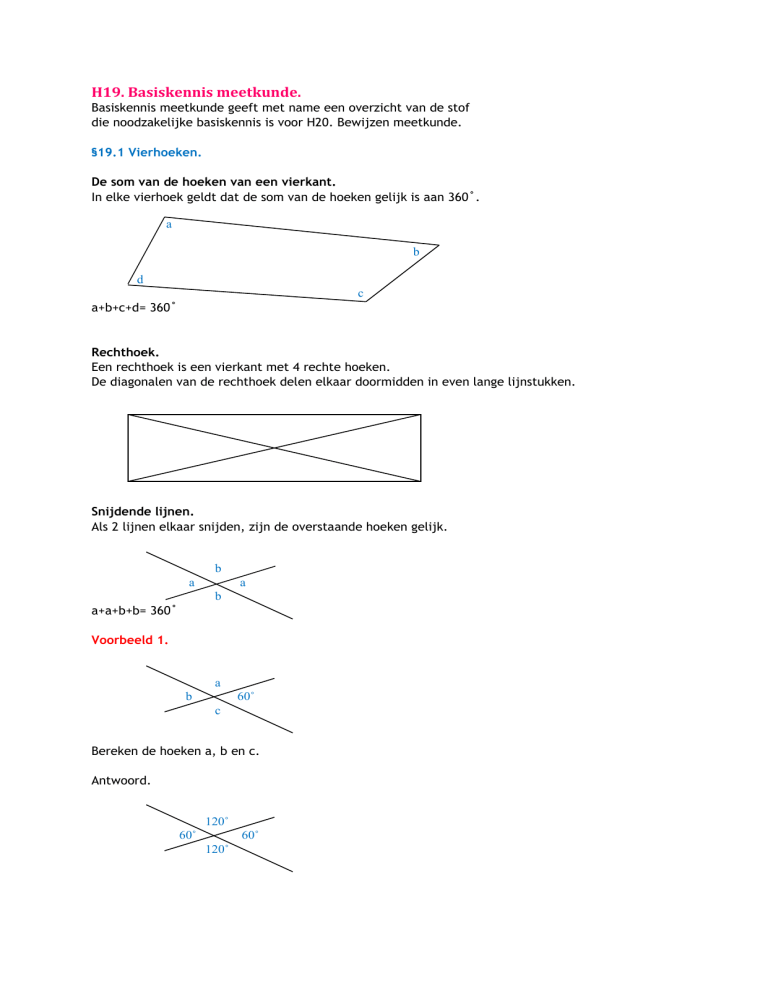
In elke vierhoek geldt dat de som van de hoeken gelijk is aan 360˚.
a
b
d
c
a+b+c+d= 360˚
Rechthoek.
Een rechthoek is een vierkant met 4 rechte hoeken.
De diagonalen van de rechthoek delen elkaar doormidden in even lange lijnstukken.
Snijdende lijnen.
Als 2 lijnen elkaar snijden, zijn de overstaande hoeken gelijk.
b
a
a
b
a+a+b+b= 360˚
Voorbeeld 1.
a
b
60˚
c
Bereken de hoeken a, b en c.
Antwoord.
120˚
60˚
60˚
120˚
§19.2 Driehoeken.
Som van de hoeken van een driehoek is 180˚.
b
a
c
a+b+c= 180˚
Stelling van Pythagoras.
Stelling van Pythagoras: a2 + b2= c2
Voorwaarde: Rechte hoek in C.
A
c
B
b
a
C
Bekende standaardverhoudingen:
13
5
5
4
3
12
Cosinusregel.
In elke driehoek geldt: c2= a2 + b2 – 2abcos γ
α
c
b
β
γ
a
Er geldt:
c2= a2 + b2 – 2abcos γ
a2= b2 + c2 – 2abcos α
b2= a2 + c2 – 2abcos β
Sinusregel.
a / sin α= b / sin β= c / sin γ
Gelijkvormige driehoeken.
Voor gelijkvormig driehoeken geldt dat de zijden gelijke verhoudingen hebben.
c
b
cx
bx
a
ax
Voorbeeld 2.
2 gelijkvormige driehoeken zijn gegegeven.
Bereken lengte van a en b.
5
4
b
6
3
a
Antwoord.
6/4= 1,5
a= 1,5 . 3= 4,5
b= 1,5 . 5= 7,5
Gelijkbenige driehoek.
2 driehoeken zijn gelijkbenig als één van de volgende voorwaarden geldt.
- Twee hoeken zijn gelijk: α=α
- De overliggende zijden zijn gelijk: A=A
Als α=α -> A=A
Als A=A -> α=α
A
α
A
α
Voorbeeld 3.
Van de volgende gelijkbenige driehoek zijn de volgende gegevens bekend.
6,3
20˚
c
Bereken de omvang van alle zijden en hoeken.
Antwoord.
Gelijke hoeken, dus 20˚ en 140˚.
Gelijke zijden, dus ook 6,3.
Sinusregel:
sin 20˚/ 6,3= sin 180˚/ c ->
0,054= 0,643 / c ->
c= 0,643 / 0,054= 11,91
6,3
140˚
20˚
6,3
11,91
20˚
Omgeschreven driehoek.
Je tekent een driehoek om een driehoek door lijnen te gebruiken
die evenwijdig lopen aan de overliggende lijnen van de start driehoek.
De hoeken van de start driehoek delen de omliggende lijnen doormidden.
C
A
A’
B
C
B’
A
B
C’
§19.3 Cirkel.
Cirkel heeft middelpunt M met straal r.
De cirkel geeft alle punten met afstand r van het middenpunt M.
r
M
r
Eigenschappen van een cirkel:
- Omtrek= 2πr
- Oppervlakte= πr2
Bij gelijke bogen horen gelijke koorden:
Als b=b -> a=a.
a
a
b
b
Loodlijn vanuit M op de koorde deelt de koorde middendoor.
M
M
a
a
Raaklijn staat loodrecht op de lijn vanuit het midden van de cirkel.
M
┘
Omtrekshoek en middelpuntshoek.
Als ABC op een cirkel liggen, is ACB de omtrekshoek en is ACM de middelpuntshoek.
C
A
B
M
Omgeschreven cirkel
Cirkel rond driehoek.
Ingeschreven cirkel.
Cirkel binnen driehoek.
C
K
A
B
L
M
M
N
AM= BM= CM
Voetpunten: K, L en N
KM= LM= NM
Voetpunten.
Een lijnstuk vanuit M op een voetpunt, maakt een rechte hoek.
K
L
M
N
H20 Bewijzen meetkunde.
§20.1 De stelling van de 3 middelloodlijnen van een driehoek.
De middelloodlijn is de lijn van punten die even ver liggen van A en B.
A●
A●
●B
B●
- De stelling van de 3 middelloodlijnen van een driehoek.
De drie middelloodlijnen van de lijnstukken AB, BC en CA gaan door
hetzelfde punt M. M is het midden van de omgeschreven cirkel, dus AM=BM=CM.
C
C
C
M
A
B
M
A
B
A
B
- Gegeven zijn 2 van de 3 middelloodlijnen en je moet bewijzen
dat de derde middelloodlijn ook door M gaat.
C
M
A
B
Als je kan bewijzen dat AM=CM volgt dat de middelloodlijn door M gaat
(want dan A en C even ver van M= definitie van loodlijn).
Bewijs 1.
Identiek Bewijs 2
M
M
A
B
B
AM=BM
want loodlijn AB door M
BM=CM
want loodlijn BC door M
AM=BM en BM=CM ->
Dus: AM=CM
BM=CM en AM=BM ->
Dus: AM=CM
C
§20.2 De stelling van de 3 deellijnen van een driehoek.
De deellijn is de lijn die de hoek door midden deelt.
Alle punten op de deellijn liggen even ver af van de aanliggende zijden van de hoek.
*
*
De stelling van de 3 deellijnen van een driehoek.
De drie deellijnen van hoekpunten A, B, en C gaan door hetzelfde punt M.
M is het midden van de ingeschreven cirkel,
dus als K, L en N de voetpunten geldt: KM=LM=NM.
C
C
--
C
N
M
L
M
+
B
+
B
B
K
* *
A
A
A
- Gegeven zijn 2 van de 3 deellijnen en de 3 voetpunten en
je moet bewijzen dat de derde deellijn ook door M gaat (Plaatje A).
Plaatje A.
Plaatje B.
Plaatje C.
C
C
N
L
C
**
N
M
L
N
L
M
*
B
*
K
A
M
B
B
K
A
K
A
Als je kan bewijzen dat MK=MN volgt dat de deellijn uit A door M gaat,
want dan voetpunten K en N even ver van M (=definitie deellijn).
ΔKMB en ΔLMB zijn congruente driehoeken.
2 gelijke hoeken (rechte hoek bij voetpunten L en M + B)
en een gelijke zijde (MB) en dus gelijke driehoek: MK=ML (Plaatje B).
ΔLMC en ΔNMC zijn congruente driehoeken.
2 gelijke hoeken (rechte hoek bij voetpunten L en N + C)
en een gelijke zijde (MC) en dus gelijke driehoek: ML=MN (Plaatje C).
MK=ML en ML=MN -> MK=MN
§20.3 De stelling van de 3 zwaartelijnen van een driehoek.
De zwaartelijn gaat vanuit hoekpunt A naar midden van overliggende zijde.
A
a
a
A
a
a
- De stelling van de 3 zwaartelijnen van een driehoek.
De drie deellijnen van hoeken A, B, en C gaan door hetzelfde punt S.
S deelt de zwaartelijnen doormidden in een verhouding 2:1
C
R
CS:SP= 2:1
BS:SR= 2:1
AS:SQ= 2:1
Q
S
A
B
P
Gegeven zijn:
Driehoek ABC met zwaartelijnen AQ en CP door S1 (driehoek 1).
Driehoek ABC met zwaartelijnen BR en CP door S2 (driehoek 2).
Bewijs S1=S2
Driehoek 1
Driehoek 2
C
C
b
c
Q
S1
A
a
P
R
b
a
c
B
A
S2
a
P
a
B
Driehoek 1:
Trek Q naar AB evenwijdig aan CP
(dus gelijkvormige driehoeken AS1P met AQQ´ met 2:3 en CPB met QQ´B met 2:1) ->
AP : PQ´ : Q´B= 2 : 1 : 1
CP : QQ`= 2 : 1
QQ´ : S1P= 3 : 2
Stel QQ´= 3a ->
S1P= 2a en CP= 6a.
Als CP=6a en S1P=2a -> CS1=4a
CS1 : S1P= 2
Driehoek 1.
C
b
Q
S1
A
a
2
b
P a’ Q’ a’ B
: 1 :
1
Driehoek 2:
Trek R naar AB evenwijdig aan CP
(dus gelijkvormige driehoeken BS2P met BRR´ met 2:3 en CPA met RR´A met 2:1) ->
BP : PR´ : R´A= 2 : 1 : 1
CP : RR`= 2 : 1
RR´ : S2P= 3 : 2
Stel RR´= 3a ->
S2P= 2a en CP= 6a.
Als CP=6a en S2P=2a -> CS2=4a
CS2 : S2P= 2
Driehoek 2.
C
c
R
c
S2
A a’ R’ a’ P
1 :
1 :
CS1 : S1P= 2
CS2 : S2P= 2 ->
S1= S2
a
2
B
§20.4 De stelling van de 3 hoogtelijnen van een driehoek.
De hoogtelijn gaat vanuit een hoekpunt A loodrecht naar de tegenoverliggende zijde.
A
∟
- De stelling van de 3 hoogtelijnen van een driehoek.
De drie hoogtelijnen gaan door hetzelfde punt.
Gegeven zijn de 3 hoogtelijnen en je moet bewijzen dat 3 lijnen
door hetzelfde punt gaan.
C
A
∟
B
Teken een driehoek rond de driehoek met AC evenwijdig aan A´C´ etc.
Zie voor eigenschappen basiskennis meetkunde (omgeschreven driehoek).
B’
C
A’
D
E
B
F
A
C’
BE loodrecht op AC en dus ook op A´C´ en dus middelloodlijn op A´C´.
AD loodrecht op BC en dus ook op B´C´ en dus middelloodlijn op B´C´.
CF loodrecht op AB en dus ook op A´B´ en dus middelloodlijn op A´B´.
Dus 3 middelloodlijnen en 3 middelloodlijnen van een driehoek gaan door hetzelfde punt.
B’
A’
C’
§20.5 Koordenvierhoek.
Als ABCD in die volgorde op een cirkel liggen, is ABCD een koordenvierhoek.
D
C
A
B
Koordenvierhoekstelling houdt in dat elk paar overliggende hoeken samen 180˚ is,
dus: A + C=180˚, B + D=180˚.
Gegeven is de koordenvierhoek ABCD.
Bewijs A + C=180˚
Trek vanuit M lijnen naar A, B, C en D
D
δ1
δ2
γ2 C
γ1
M
α1
α2
A
β2
β1
B
α2=β1, α1=δ2, β2=γ1, δ1=γ2 (want gelijkbenige driehoek)
α2 + β1 + β2 + γ1 + γ2 + δ1 + δ2 + α1= 360˚
α2 + α2 + γ1 + γ1 + γ2 + γ2 + α1 + α1= 360˚ ->
2α2 + 2γ1 + 2γ2 + 2α1= 360˚ ->
α1 + α2 + γ1 + γ1= 180˚ ->
A + C= 180˚
§20.6 Thales.
§20.6.1 Stelling van Thales.
Als in een driehoek ABC, C een rechte hoek heeft (Figuur A),
dan ligt C op een cirkel met middellijn AB (Figuur B).
Figuur B:
Figuur A:
A
A
C
B
C
Gegeven: Driehoek ABC met C=90˚
Te bewijzen: AM= BM= CM
A
M
C
B
Bewijs:
Teken een rechthoek CADB.
A
D
M
C
B
In een rechthoek zijn diagonalen even lang en snijden diagonalen elkaar doormidden.
-> AM= BM= CM
B
§20.6.2 Omgekeerde stelling van Thales.
Als AB een middellijn is op een cirkel en C ligt op de cirkel, geldt: C=90˚.
C’
C’
C’’
C
A
C
B
A
C= C´= C´´= 90˚
Te bewijzen C= 90˚
Bepaal M als midden van lijn AB en trek een lijn van M naar C
C
γ1
A α
γ2
M
β
B
α + γ1 + γ2 + β= 180˚ (som driehoek= 180˚)
α= γ1 (want gelijkbenige driehoek)
β= γ2 (want gelijkbenige driehoek)
γ1 + γ1 + γ2 + γ2= 180˚ ->
γ1 + γ2= 90˚ ->
C= 90˚
C’’
B
§20.7 Stelling van de constante hoek.
Als je tussen 2 punten op een cirkel A en C een lijn trekt,
en B ligt op de cirkelboog boven die lijn,
dan verandert ABC niet door B langs die lijn te verschuiven.
B2
B1
β2
β1
A
C
AB1C= AB2C
Bewijs β1= β2
Maak een koordenvierhoek:
B2
B1
β2
β1
A
C
δ
D
δ + β1= 180˚
δ + β2= 180˚
δ + β1= δ + β2 ->
β1= β2
§20.8 Stelling van de omtrekshoek.
De omtrekshoek is de ABC als A, B en C op een cirkel liggen.
De omtrekshoek is de helft van de middelpunthoek.
B
M
A
C
Te bewijzen: ABC= ½ AMC
Bewijs:
B
β γ
δ2
δ3
δ1
β
α
γ
α
A
α=α, β=β, γ=γ want gelijkbenige driehoek
δ1 + 2α= 180˚ -> δ1= 180˚ - 2α
δ2 + 2β= 180˚ -> δ2= 180˚ – 2β
δ3 + 2γ= 180˚ -> δ3= 180˚ - 2γ
δ1 + δ2 + δ3= 360˚ -> δ1= 360˚ - δ2 - δ3 ->
δ1= 360˚ – (180˚ - 2β) – (180˚ – 2γ) ->
δ1= 360˚ – 180˚ + 2β – 180˚ + 2γ ->
δ1= 2β + 2γ (δ1= AMC en β+γ= ABC) ->
AMC= 2 . ABC ->
ABC= ½ AMC
C
§20.9 Stelling van de raaklijnhoek.
A en B liggen op een cirkel.
De hoek tussen de koorde BA met de raaklijn in A (A2)
is de helft van de middelpuntshoek BMA.
M
1
B
Te bewijzen: A2= ½ M
Bewijs:
B1 + M + A1= 180˚ (driehoek)
B1= A1 (gelijkbenige driehoek)
A1 + M + A1= 180˚ ->
2 .  A1= 180˚ – M ->
 A1= 90˚ – ½ M
A1 + A2= 90˚ ->
A1= 90˚ – A2
 A1= 90˚ – ½ M en A1= 90˚ – A2
90˚ – ½ M= 90˚ – A2 ->
A2= ½ M
1
2
A