Oplossingen toetsmodule hoofdstuk 7: Vlakke figuren

Pienter 1ASO
Oplossingen toetsmodule hoofdstuk 7
Oplossingen toetsmodule hoofdstuk 7: Vlakke figuren
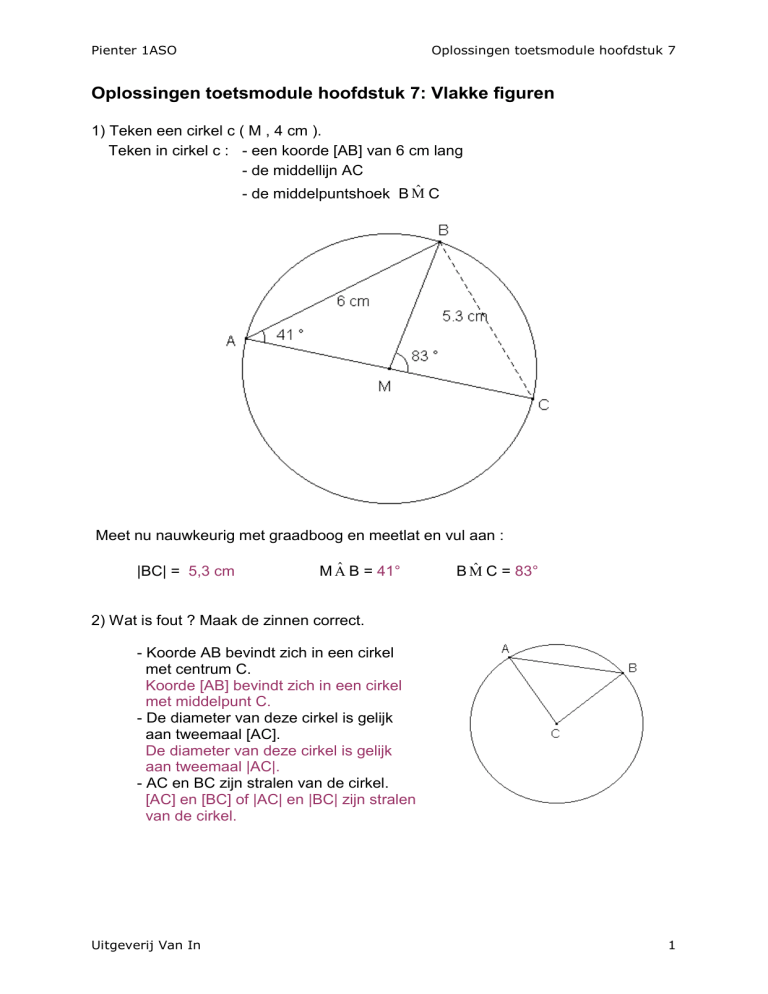
1) Teken een cirkel c ( M , 4 cm ).
Teken in cirkel c : - een koorde [AB] van 6 cm lang
- de middellijn AC
- de middelpuntshoek B M̂ C
Meet nu nauwkeurig met graadboog en meetlat en vul aan :
|BC| = 5,3 cm
M Â B = 41°
B M̂ C = 83°
2) Wat is fout ? Maak de zinnen correct.
- Koorde AB bevindt zich in een cirkel
met centrum C.
Koorde [AB] bevindt zich in een cirkel
met middelpunt C.
- De diameter van deze cirkel is gelijk
aan tweemaal [AC].
De diameter van deze cirkel is gelijk
aan tweemaal |AC|.
- AC en BC zijn stralen van de cirkel.
[AC] en [BC] of |AC| en |BC| zijn stralen
van de cirkel.
Uitgeverij Van In
1
Pienter 1ASO
Oplossingen toetsmodule hoofdstuk 7
3) Teken een lijnstuk [AB] met lengte 4 cm. Kleur alle punten die minstens
3 cm van A en hoogstens 2 cm van B liggen.
Het blauwe gebied bevat
alle punten die voldoen
aan de opgave.
4) Vul in met  of :
D  c ( A , [AB] )
B  c ( C , 3 cm )
A  c ( B , |BD| )
Controleer de antwoorden met een passer.
Vul aan : C  c ( B , |BC| of 3 cm)
A  c ( E , 4 cm )
Uitgeverij Van In
2
Pienter 1ASO
Oplossingen toetsmodule hoofdstuk 7
5) Welk soort driehoek(-en) verkrijgen we als we volgende vierhoeken
doorknippen volgens een diagonaal ? Vermeld alle mogelijkheden.
a) een rechthoek: rechthoekige driehoeken
b) een ruit: 2 scherphoekige of 2 stomphoekige gelijkbenige driehoeken
c) een vierkant: gelijkbenige rechthoekige driehoeken
d) een parallellogram: 2 scherphoekige of 2 stomphoekige driehoeken
e) een rechthoekig trapezium:
één rechthoekige driehoek + een scherphoekige of stomphoekige driehoek
f) een vlieger: 2 gelijkbenige driehoeken of 2 willekeurige driehoeken
6) Waar (W) of niet waar (NW) ? Onderzoek m.b.v. een tekening !
a)
b)
c)
d)
e)
Elk parallellogram met ten minste 1 rechte hoek is een rechthoek.
Elk trapezium met tenminste 2 rechte hoeken is een rechthoek.
Een parallellogram waarvan de zijden even lang zijn is een ruit.
Een trapezium met 4 gelijke zijden is een parallellogram.
Een trapezium heeft geen gelijke zijden.
W
NW
W
W
NW
7) Teken een gelijkbenige driehoek ABC met tophoek  = 36 ° en |AB| = 5 cm
Bereken : B̂ = Ĉ = (180° - 36°):2
= 72 °
Meet : |BC| = 3,1 cm
8) Teken driehoek BAF met |BA| = 5 cm , B̂ = 45 ° en F̂ = 75 °.
 = 180° - 45° - 75° = 60°
Meet nauwkeurig en vul aan
|BF| = 4,5 cm |AF| = 3,7 cm
Uitgeverij Van In
3
Pienter 1ASO
Oplossingen toetsmodule hoofdstuk 7
9) Bereken de grootte van de aangeduide hoeken. (Niet meten!)
60°
50°
60°
60°
120°
80°
30°
50°
- hoeken in een gelijkzijdige driehoek
- nevenhoeken
- som van de hoeken in een vierhoek
- scherpe hoeken in een rechthoekige driehoek
- nevenhoeken
- basishoeken in een gelijkbenige driehoek
10) In driehoek ABC is AH een hoogtelijn, BM een zwaartelijn, CS de deellijn van
hoek Ĉ en EF de middelloodlijn van [BC].
Vul de juiste benaming in voor volgende merkwaardige lijnen :
a)
b)
c)
d)
e)
f)
g)
h)
in driehoek ABC is AE een zwaartelijn
in driehoek ACH is AH een hoogtelijn
in driehoek BMC is EF een middelloodlijn
in driehoek CHW is WE een hoogtelijn
in driehoek ACH is HM een zwaartelijn
in driehoek CEA is CW een deellijn
in driehoek FHC is FE een hoogtelijn
in driehoek BMC is ME een zwaartelijn
11) Teken een driehoek zodanig dat
rechten a, b en c de drie hoogtelijnen
zijn.
Teken een loodlijn op a, b of c.
De snijpunten met de twee ander rechten
zijn dan twee hoekpunten van de
driehoek. Teken door deze hoekpunten
de bijhorende loodlijnen.
Uitgeverij Van In
4