Oefening 6

1ste Kandidatuur ARTS of TANDARTS
Academiejaar 2002-2003
BIOFYSICA: WERKZITTING 2 (Oplossingen)
DYNAMICA
Oefening 6
Een blok met massa 20 kg rust op een horizontaal vlak. De wrijvingscoëfficiënt tussen de blok en het vlak is 0,6. Wat is de grootte van de
minimale horizontale kracht die het blok in beweging kan brengen ?
Met de minimale horizontale krachtgrootte wordt de grootte van de kracht bedoeld waarmee je aan het blok moet trekken om het net in beweging te brengen
(d.w.z. een heel klein beetje minder hard trekken zou het blok niet doen bewegen, en
een klein beetje meer zou het blok wel doen bewegen). Op dat ogenblik balanceren
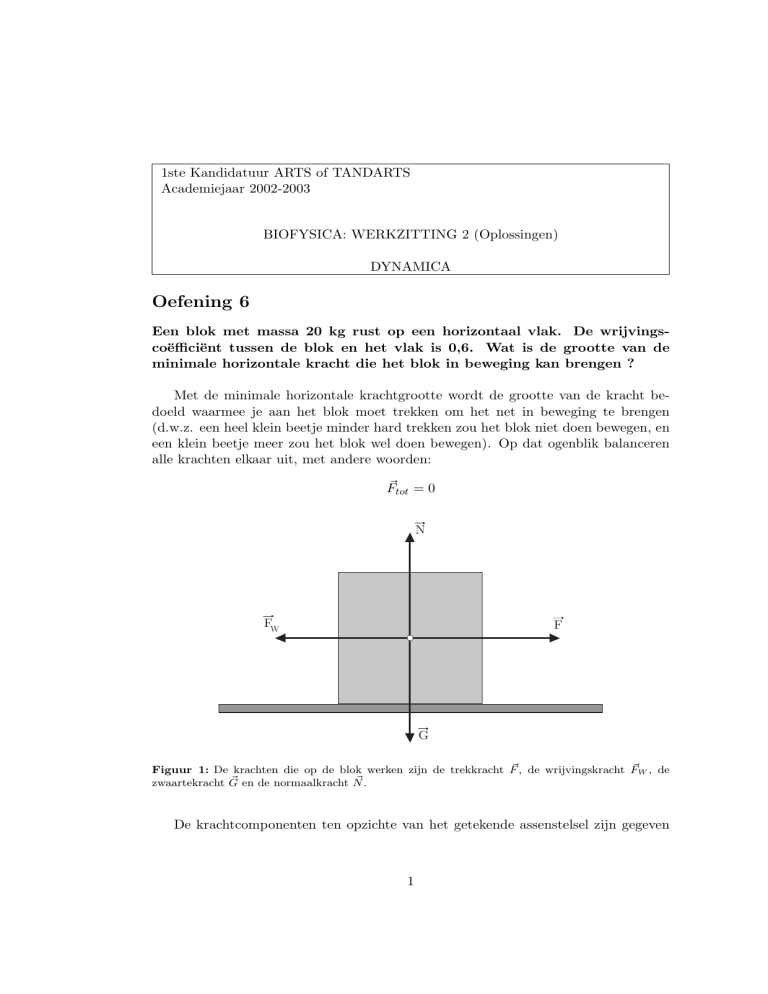
alle krachten elkaar uit, met andere woorden:
Ftot = 0
N
FW
F
G
, de wrijvingskracht F
W , de
Figuur 1: De krachten die op de blok werken zijn de trekkracht F
en de normaalkracht N
.
zwaartekracht G
De krachtcomponenten ten opzichte van het getekende assenstelsel zijn gegeven
1
door:
= 0 , −mg
G
F = F , 0
FW
= 0, N
N
= −fN, 0
De som van alle krachten is gegeven door:
+N
+ F + FW = 0
Ftot = 0 ⇔ G
⇔
⇔
⇔
Gx + Nx + Fx + FW x = 0
Gy + Ny + Fy + FW y = 0
−f N + F = 0
−mg + N = 0
F =fN
N = mg
zodat de vereiste grootte F van de trekkracht gegeven is door:
F = f mg = (0, 6) · 20 · 9, 81 N = 118 N
Oefening 7
Twee blokjes, een met massa m1 en het andere met massa m2 staan tegen
elkaar op een horizontaal vlak. Er is geen wrijving tussen het vlak en de
blokjes. We duwen met een horizontale kracht F tegen het blokje met
massa m1 . Wat is de grootte van de kracht die het blokje met massa m1
uitoefent op het blokje met massa m2 ?
m1
F
m2
.
Figuur 2: Er wordt tegen het grote blok geduwd met een kracht F
Je kan best dit probleem opsplitsen in twee problemen voor elk blokje apart.
Hierbij moet je echter wel opletten dat je de derde wet van Newton niet vergeet
2
toe te passen om de actie- en reactiekrachten in rekening te brengen. De volgende
krachten werken op elk blokje in:
3
N1
m1
F12
F
N2
m2
F21
G2
G1
, de zwaartekracht G
1 en de
Figuur 3: De krachten die op de blok m1 werken zijn de duwkracht F
12 van het
1 . Bovendien is er wegens de derde wet van Newton een reactiekracht F
normaalkracht N
21 .
blokje m2 op de eerste blok m1 . Op het blokje m2 werkt horizontaal enkel de reactiekracht F
De reactiekracht F21 is net de kracht die blokje 1 op blokje 2 uitoefent. Het is de
bedoeling de grootte van deze kracht te bepalen. Je kan hiervoor best de tweede wet
van Newton voor elk blokje apart uitschrijven:
• Blokje met massa m1
1 + G
1 = m1a1
Ftot = m1a1 ⇔ F + F12 + N
F − F12 = m1 a1,x
⇔
N1 − m1 g = m1 a1,y
• Blokje met massa m2
2 + G
2 = m2a2
Ftot = m2a2 ⇔ F21 + N
F21 = m2 a2,x
⇔
N2 − m2 g = m2 a2,y
Wegens de derde wet van Newton weet je dat F12 = F21 . Als je de twee vergelijkingen
voor de x-componenten optelt vind je daarom:
+
F − F12 = m1 ax,1
F21 = m2 ax,2
F = m1 ax,1 + m2 ax,2
Bovendien weet je dat a1,x = a2,x . Als de versnellingen verschillend zouden zijn,
bijvoorbeeld als de versnelling a2,x van het tweede blokje groter zou zijn dan die
4
van het eerste blokje, dan zou het tweede blokje sneller wegbewegen dan het eerste
(een grotere versnelling wil ook zeggen dat de snelheid vlugger toeneemt!). Omdat
je enkel tegen het eerste blokje duwt, verwacht je niet dat het tweede blokje zomaar
er vandoor kan gaan.
Noteer de versnelling van de blokjes in de x-richting door ax = a1,x = a2,x , dan
vind je dus:
F = (m1 + m2 )ax
Uit de x-vergelijking voor blokje 2 weet je echter dat F21 = m2 ax , dus kan je ax in
de bovenstaande formule vervangen:
F = (m1 + m2 )
F21
m2
Zodat je als eindresultaat voor de grootte F21 vindt dat:
F21 =
m2
F
m1 + m2
Oefening 8
Een kubus met massa 800 g start vanuit rust en glijdt zonder wrijving van
een helling die een hoek van 30◦ maakt met het horizontaal vlak. Aan de
voet van de helling heeft de kubus een snelheid van 12 m/s. De hoogte
van dit eindpunt van de helling is 4 m. Wat is de versnelling van de kubus
op het hellend vlak ? Wat is de lengte van de helling ? Waar treft de
kubus de grond na de val ?
30°
∆x
Figuur 4: Het blokje glijdt van de helling, en valt daarna vanop een hoogte van 4 m naar beneden.
5
Je kan best het probleem opsplitsen in twee deelproblemen: eerst beschrijf je de
beweging op de schuine helling, en daarna bestudeer je los daarvan de valbeweging.
• 1. De beweging op de helling
en de normaalDe krachten die op het systeem werken zijn de zwaartekracht G
kracht N (die loodrecht op het bewegingsvlak staat en dus hier de zwaartekracht
niet volledig compenseert!). Om de berekeningen eenvoudig te houden, kies je
het assenstelsel waarin je het probleem gaat oplossen best op het vertrekpunt
van het blokje, met de x-as volgens de helling en de y-as er loodrecht op.
y
N
30°
x
G
L
en de norFiguur 5: Wanneer het blokje van de helling glijdt, werken enkel de zwaartekracht G
maalkracht N op het blokje. De lengte van de helling wordt met L genoteerd.
In dit assenstelsel hebben de vectoren de volgende componentschrijfwijze:
= 0, N
= mg cos(60◦ ) , −mg sin(60◦ )
N
G
De tweede wet van Newton kan je dus uitschrijven in componenten:
mg cos(60◦ ) + 0 = max
+N
= ma
F = G
⇔
−mg sin(60◦ ) + N = may
Aangezien het deeltje alleen volgens de x-as beweegt en zo blijft bewegen mag
er geen versnelling in de y-richting zijn, dus je weet bovendien dat ay = 0. Uit
de tweede wet van Newton haal je zo dat:
ax = g cos(60◦ )
ay = 0
6
Aangezien deze twee componenten van de versnelling constant zijn in de tijd,
is ook de hele versnellingsvector a constant in de tijd. Je mag dus de formules
voor de eenparig veranderlijke beweging gebruiken:
r(t) = r0 + v0 t +
at2
2
v (t) = v0 + at
In componenten zijn deze vergelijkingen

a t2


 x(t) = x0 + v0,x t + x
vx (t) = v0,x + ax t
2
2

vy (t) = v0,y + ay t

 y(t) = y0 + v0,y t + ay t
2
Omdat je de oorsprong van het assenstelsel op de beginpositie van het blokje
gekozen hebt, is r0 = 0, of in componenten: x0 = 0 en y0 = 0. Ook de
beginsnelheid v0 = 0, omdat we aannemen dat het blokje vanuit rust vertrekt.
De uitdrukkingen voor de versnellingscomponenten zijn ook gekend, dus je kan
de vergelijkingen expliciet uitschrijven:

◦
 x(t) = g cos(60 ) t2
vx (t) = g cos(60◦ )t
2

vy (t) = 0
y(t) = 0
Noteer het tijdstip waarop het blokje het einde van de helling bereikt als tf .
Je weet dat op dat ogenblik de snelheid als grootte 12 m/s heeft, maar omdat
de snelheid in de y-richting altijd nul is, weet je ook dat v (tf ) = v(tf ) =
vx (tf ) = 12 m/s. Op tijdstip tf geldt met andere woorden dat:
vx (tf ) = g cos(60◦ )tf
⇒
tf =
vx (tf )
g cos(60◦ )
De x-positie op dat tijdstip is gegeven door x(tf ). Op het moment dat het blokje
het einde van de helling bereikt, heeft het echter in de x-richting net de lengte
van de helling afgelegd. Immers, de lengte van de helling L = x(tf ) − x(0) =
x(tf ) (aangezien x(0) = 0 door de keuze van het assenstelsel). De lengte van
de helling is daarom gegeven door:
L = x(tf )
g cos(60◦ ) 2
=
tf
2
2
vx (tf )
g cos(60◦ )
=
2
g cos(60◦ )
vx (tf )2
=
2g cos(60◦ )
(12 m/s)2
=
2 · (9, 81 m/s2 ) · cos(60◦ )
= 14, 7 m
7
• 2. De valbeweging
op het blokje. Om deze
Tijdens het vallen werkt enkel de zwaartekracht G
beschrijving eenvoudig te maken, kan je hier het assenstelsel zodanig kiezen
dat de x-as horizontaal loopt en de y-as vertikaal. Dit kan je doen omdat je
de valbeweging los van de schuifbeweging (waar een ander assenstelsel gebruikt
werd) beschrijft.
y
x
30°
v1
G
∆x
Figuur 6: Het blokje begint de valbeweging met de eindsnelheid v1 van de schuifbeweging op de
op het blokje.
helling. Daarna werkt enkel de zwaartekracht G
Uit de tweede wet van Newton haal je meteen dat ax = 0 en ay = −g. De
versnellingsvector a is met andere woorden ook hier constant, en je mag opnieuw
de formules van de eenparig veranderlijke beweging gebruiken:


ax t2


 x(t) = x0 + v0,x
 x(t) = v0,x t
t+
2
2
⇔

 y(t) = v t − gt
a
t2
y

0,y
 y(t) = y0 + v0,y
t+
2
2
Hierbij is gebruikt dat x0 = y0 = 0 omdat je de oorsprong van het assenstelsel weer op de vertrekpositie van het blokje gelegd hebt. Je moet nu nog
een uitdrukking vinden voor de beginsnelheid v0 . Het blokje begint echter de
valbeweging als de beweging op de schuine helling afgelopen is, dus de eindsnelheid v (tf ) bij de schuifbeweging is net gelijk aan de beginsnelheid v0 van
de valbeweging. Je weet dus dat de beginsnelheid een vector is met grootte 12
m/s, die een hoek van 30◦ graden maakt met de horizontale, volgens de schuine
helling. Deze vector is daarom gegeven door:
v0 = 12 cos(30◦ ) , −12 sin(30◦ )
8
De positie van het blokje bij het vallen wordt dus beschreven door:

◦
 x(t) = 12 cos(30 )t
2
 y(t) = −12 sin(30◦ )t − gt
2
Uit de vergelijking voor y(t) kan je de tijd tv halen die het blokje nodig heeft
om op de grond te vallen. Je weet immers dat ten opzichte van de gekozen
oorsprong het blokje 4 m lager terechtkomt, dus als het de grond raakt is de ycoördinaat van het blokje gelijk aan y(tv ) = −4 m. De tijd tv kan dan berekend
worden als volgt:
y(tv ) = −4 m ⇔ −12 sin(30◦ )tv −
gt2v
= −4
2
gt2v
+ 12 sin(30◦ )tv − 4 = 0
2
−12 sin(30◦ ) ± (12 sin(30◦ ))2 + 8g
⇔ tv =
g
−1, 70 s
⇔ tv =
0, 48 s
⇔
Aangezien het blokje de grond niet kan raken voor het begonnen is met vallen,
moet je de oplossing −1, 70 s verwerpen. Nudat de tijd gekend is die het blokje
nodig heeft om te vallen, kan je ook de x-positie van het blokje berekenen op
het ogenblik dat het de grond raakt. Deze positie is gegeven door x(tv ), maar
deze positie is net gelijk aan de gezochte afstand ∆x. Met andere woorden:
∆x = x(tv )
= 12 cos(30◦ )tv
= (12 cos(30◦ ) m/s)(0, 48 s)
= 4, 99 m
Oefening 10
In de figuur wordt een schema gegeven van een experiment. Een α-deeltje
(4 He-kern) wordt met een snelheid van 20000 m/s in een elektrisch veld
met grootte 4000 N/C geschoten en hierdoor afgebogen. Even later valt
het deeltje in op een trefplaatje. Bereken de afstand Y als d = 5 mm en
D = 3 cm.
Je kan ook hier best het probleem opsplitsen in twee deelproblemen: eerst bestudeer je wat er gebeurt wanneer het α-deeltje zich in het elektrisch veld bevindt, en
daarna hoe het deeltje verder beweegt als het het elektrisch veld verlaten heeft.
9
Y
v0
E
d
D
Figuur 7: Met een gegeven beginsnelheid buigt het α-deeltje af in het elektrisch veld. Eens het
deeltje het veld verlaten heeft, volgt het een rechte (aangezien de snelheid constant blijft).
Als je wil berekenen op welke hoogte Y het deeltje de plaat treft, moet je weten
met welke beginpositie en -snelheid het deeltje uit het elektrisch veld komt. Buiten
het elektrisch veld werkt er immers geen kracht meer op het deeltje1 zodat je wegens
de eerste wet van Newton weet dat het deeltje buiten het veld volgens een rechte lijn
gaat bewegen. Kennis van de beginsnelheid en -positie is voldoende om dan te weten
waar het deeltje terecht zal komen.
• 1. Binnen het elektrisch veld E
De afbuiging van het deeltje ten gevolge van het elektrisch veld kan berekend
worden met de tweede wet van Newton. De kracht op een deeltje met lading q
is immers gegeven door F = q E.
De tweede wet van
in een elektrisch veld E
Newton levert:
q F = ma ⇔ a = E
m
Aangezien het elektrisch veld constant is, is ook de versnelling constant. Je
1
De zwaartekracht wordt hier verwaarloosd. Je weet immers dat de zwaartekracht voor een 4 He is de krachtgrootte
kern van grootte mg ≈ 4mp g ≈ 9 · 10−26 N is. Binnen het elektrisch veld E
ongeveer qE = 2eE ≈ 10−14 N . De invloed van de zwaartekracht is dus ongeveer 1012 keer kleiner,
en de zwaartekracht in rekening brengen levert dus maar een verbetering van 10−12 op de nauwkeurigheid van de berekening (d.w.z. dat je al 12 cijfers na de komma moet narekenen vooraleer je een
verschil ziet).
10
mag dus de formules voor een eenparig veranderlijke beweging gebruiken:


 vx (t) = v0
 x(t) = x0 + v0 t
 vy (t) = qE t
 y(t) = y0 + qE t2
2m
m
= (0, E) en v0 = (v0 , 0) in het gekozen assenstelsel (zie figuur).
aangezien E
y
vf
x
v0
E
d
= q E.
De snelheid
Figuur 8: In het elektrisch veld wordt het deeltje afgebogen door de kracht F
verandert, en bij het verlaten van het elektrisch veld noteren we de snelheid van het deeltje vf .
Om te weten op welke positie het deeltje het elektrisch veld verlaat, moet je
enkel de y-positie nog bepalen (aangezien het elektrisch veld stopt op x = d).
Daarvoor heb je de tijd tf nodig die het deeltje in het elektrisch veld doorbrengt.
Je weet echter dat het deeltje op een tijd tf in de x-richting een afstand d aflegt,
dus:
d
x(tf ) = d
⇔
v0 t f = d
⇔
tf =
v0
De positie rf waarop het deeltje het veld verlaat is dus gegeven door:
rf = x(tf ) , y(tf ) =
qE d2
d,
2m v02
Het α-deeltje verlaat het veld met een snelheid vf gegeven door:
qE d
vf = vx (tf ) , vy (tf ) = v0 ,
m v0
11
• 2. Buiten het elektrisch veld E
Er werken hier geen krachten op het α-deeltje, zodat uit F = ma volgt dat
a = 0. De versnelling is hier dus weer een constante vector, dus je kan weer
de formules voor de eenparig veranderlijke beweging gebruiken. Kies het assenstelsel in de beginpositie van het deeltje (in deze situatie is dat de eindpositie
binnen het elektrisch veld), dan weet je dat de beginpositie gegeven is door
r0 = 0 en de beginsnelheid door vf (= de eindpositie binnen het elektrisch
veld).

 x(t) = v0 t
x(t) = (vf )x t
⇔
qE d
 y(t) =
y(t) = (vf )y t
t
m v0
y
Y2
vf
Y
x
Y1
E
D
Figuur 9: Buiten het elektrisch veld werken er geen krachten meer op het deeltje. De snelheid vf
die het deeltje heeft bij het verlaten van het elektrisch veld blijft tijdens de resterende beweging
behouden.
De tijd ti die het deeltje nodig heeft om de afstand tussen het veld en de
trefplaat te overbruggen, kan je bepalen door je te realiseren dat het deeltje op
die tijd ti in de x-richting een afstand D overbrugt:
⇔
x(ti ) = D
ti =
D
v0
De totale verandering in de y-richting buiten het veld is daarom gegeven door:
Y2 = y(ti ) =
12
qE d D
m v0 v0
De plaats waar het deeltje de trefplaat raakt is in de y-richting gegeven door Y =
Y1 + Y2 , waarbij Y1 de afbuiging in de y-richting is door het elektrische veld. Het
eindresultaat is daarom:


X = d + D
qEd qE d2 qE d D

d + 2D
+
=
Y =
2
2
2m v0
m v0 v0
2mv0
Om een numerieke uitkomst te vinden moet je nog weten wat de lading en de massa
van een 4 He-kern zijn. Omdat een 4 He-kern bestaat uit 2 protonen (elk met lading
+e en massa mp ) en 2 neutronen (met lading 0 en massa mn ≈ mp ), weet je dat
de lading q = 2e en de massa ongeveer 4mp . Gebruik makend van het feit dat
e = 1, 602 · 10−19 C en mp = 1, 67 · 10−27 kg vind je:
X = 3, 5 · 10−2 m
Y = 8 · 10−2 m
Oefening 11
Een boogschutter mikt naar een doelwit op ooghoogte dat 50 m ver staat.
De beginsnelheid van een pijl is 70 m/s. Onder welke hoek met de horizontale moet de pijl gericht worden om het doel te raken ? Wat is de
grootste hoogte van de pijl ? Hoe lang doet de pijl erover om het doelwit
te bereiken ?
y
v0
α
x
Figuur 10: De hoek α moet zodanig zijn dat de pijl het doelwit in de roos raakt.
De tweede wet van Newton
De enige kracht op de pijl is de zwaartekracht G.
geeft daarom een versnelling ax = 0 en een versnelling ay = −g. Door de keuze
van het assenstelsel (zie figuur) is de beginpositie x0 = y0 = 0 en de beginsnelheid
13
(v0 )x = v0 cos(α) en (v0 )y = v0 sin(α). De versnelling is constant dus de formules
voor de eenparig versnelde beweging mogen gebruikt worden:

 x(t) = v0 cos(α)t
g
 y(t) = v0 sin(α)t − t2
2
Uit de formule voor x(t) kan je een uitdrukking voor de tijd ti die de pijl nodig heeft,
vinden. Je weet immers dat op het tijdstip van impact ti de pijl in de x-richting een
afstand van 50 m heeft afgelegd. Daarom:
x(ti ) = 50
⇔
ti =
50
v0 cos(α)
Op het moment van impact ti weet je bovendien dat de hoogte van de pijl y(ti ) = 0
m. Door de formule voor ti in te vullen in de uitdrukking voor y(t) vind je:
gt2i
=0
2
2
g
50
50
=
⇔ v0 sin(α)
v0 cos(α)
2 v0 cos(α)
50
g
⇔ sin(α) =
2
2 v0 cos(α)
25g
⇔ sin(α) cos(α) = 2
v0
y(ti ) = 0 ⇔ v0 sin(α)ti −
Gebruik nu dat sin(2α) = 2 sin(α) cos(α):
2 sin(α) cos(α) = 2 ·
25g
v02
50g
v02
50g
1
⇔ α = Bgsin
2
v02
⇔ sin(2α) =
Deze laatste vergelijking heeft twee oplossingen2 voor α:
α1 = 2, 87◦
α2 = 87, 1◦
De grootste hoogte kan je vonden door te kijken wanneer de kromme y(t) een
maximum heeft. Het zoeken van een maximum doe je door de afgeleide gelijk aan
nul te stellen: dy
dt = 0. Merk op dat dit overeenkomt met het zoeken naar het punt
2
Dat er twee oplossingen moeten zijn kan je inzien als volgt: de fysisch mogelijke waarden voor α
zijn deze waarbij α ∈ [0, π2 ]. Hieruit volgt echter dat 2α ∈ [0, π]. Op het interval [0, π] komen echter
met een gegeven sinuswaarde a = sin(2α) twee waarden van 2α overeen (schets de sinus en overtuig
jezelf ervan dat er twee hoeken in [0, π] zijn die op de y-as een waarde a ∈ [0, 1] aannemen). Twee
oplossingen voor 2α betekent natuurlijk ook twee oplossingen voor α zelf.
14
waarop de snelheid in de y-richting nul is! Het tijdstip th waarop de pijl op z’n hoogst
is, vind je uit
vy (th ) = 0
⇔
v0 sin(α) − gth = 0
⇔
th =
v0 sin(α)
g
De maximum hoogte y(th ) is dan gegeven door
g 2
v0 sin(α) g v0 sin(α) 2
y(th ) = v0 sin(α)th − th ⇔ y(th ) = v0 sin(α)
−
2
g
2
g
2
v0 sin(α)
⇔ y(th ) =
2g
Voor α = 2, 87◦
y(th ) = 0, 62 m
⇔
y(th ) = 249, 10 m
Voor α = 87, 1◦
Oefening 13
Een rotor is een kermisattractie waarin personen plaatsnemen tegen de
want van een holle cilinder. Die wordt daarna met een grote snelheid aan
het draaien gebracht om de cilinderas. Als de snelheid voldoende groot
is, laat men de vloer zakken, en blijven de personen tegen de wand plakken. Welke hoeksnelheid moet een rotor moet straal 5 m hebben opdat
de personen niet naar beneden zouden schuiven ? De wrijvingscoëfficiënt
tussen de personen en de wand is 0,4.
Kies een assenstelsel op de persoon in de rotor, waarbij de x-as steeds in de
normale richting ligt en de y-as omhoog gericht is. De krachten die op de persoon
de normaalkracht N
en de wrijvingskracht Fw .
inwerken zijn de zwaartekracht G,
De wrijvingskracht voorkomt dat personen naar beneden schuiven, dus moet deze
naar boven gericht staan. De tweede wet van Newton uitschrijven in het gekozen
assenstelsel levert:
+N
+ Fw = ma
Ftot = ma ⇔ G
N = man
⇔
f N − mg = may
(normale richting, x-as)
(vertikale richting, y-as)
Aangezien de persoon niet naar beneden schuift, is de versnelling in de y-richting
gelijk aan nul. Bovendien weet je dat in de normaalrichting de grootte van de (centripetaal)versnelling gegeven is door
an = Rω 2
aangezien het hier om een cirkelbeweging gaat. Invullen in de vergelijkingen levert:
N = mRω 2
mg
g
⇔
ω2 =
⇔
mRω 2 = N =
f
f
R
f N − mg = 0
15
ω
y
Fw
Fw
Fn
Fn
x
G
G
de centripetaalkracht F
n en de
Figuur 11: De krachten op de persoon zijn de zwaartekracht G,
w .
wrijvingskracht F
Zodat je als eindresultaat vindt dat, om alle krachten te balanceren zodat ay = 0, de
hoekfrequentie van de rotor gegeven moet zijn door
g
= 2, 21 rad/s
ω=
fR
Merk op dat deze hoekfrequentie overeenkomt met een snelheid v = ωR van ongeveer
11 m/s ≈ 40 km/h.
Tim Jacobs - 27 oktober 2002
16
Appendix: Werkschema voor problemen in de dynamica
1. Schets figuur
2. Teken krachten
3. Kies assenstelsel
4. Schrijf F = ma uit componenten ten opzichte van het gekozen assenstelsel
5. Los deze vergelijkingen op
Voor het eigenlijke oplossen geldt de volgende bemerking:
• Als a een constante vector is (d.w.z. dat beide componenten constant zijn in
de tijd, en niet alleen de grootte a = a !!!), dan kan je de formules voor de
eenparig versnelde beweging gebruiken:

a t2


 x(t) = x0 + v0,x t + x
vx (t) = v0,x + ax t
2
⇔
2

vy (t) = v0,y + ay t

 y(t) = y0 + v0,y t + ay t
2
• Als a niet constant is in de tijd (omdat er bijvoorbeeld een tijdsafhankelijke kracht op het systeem werkt), dan moet je expliciet de integralen voor de
snelheid en de positie uitwerken:
t



ax (t)dt
 vx (t) = v0,x +
0
t


 vy (t) = v0,y +
ay (t)dt
0

t
t t



vx (t)dt = x0 + v0,x t +
ax (t)dt dt
x(t) = x0 +


0
0
0
t
t t




vy (t)dt = y0 + v0,y t +
ay (t)dt dt
 y(t) = y0 +
0
0
0
Merk op dat wanneer ax (t) en ay (t) gewoon constant zijn, dat je ze dan voor
de integraal mag brengen. Je vindt dan bijvoorbeeld voor de dubbele integraal
in x(t):
t t t
t t
t2
ax dt dt = ax
ds dt = ax
tdt = ax
2
0
0
0
0
0
en dit geeft precies de formule voor de eenparig veranderlijke beweging.
17