Exacte waarden bij sinus en cosinus

Exacte waarden bij sinus en cosinus
In enkele gevallen kun je vergelijkingen met sinus en cosinus exact
oplossen. Welke gevallen zijn dat?
y
y
1
1
f(x) = sin x
0,5
π
–π
–2
–1 O
–0,5
1
2
3
4
5
2π
6
3π x
7
8
9
–π
–1
1
a
b
c
d
e
2
a
b
c
d
g(x) = cos x
0,5
–2
–1 O
–0,5
1
2
3π
4
5
6 2π 7
9 3π
8
x
–1
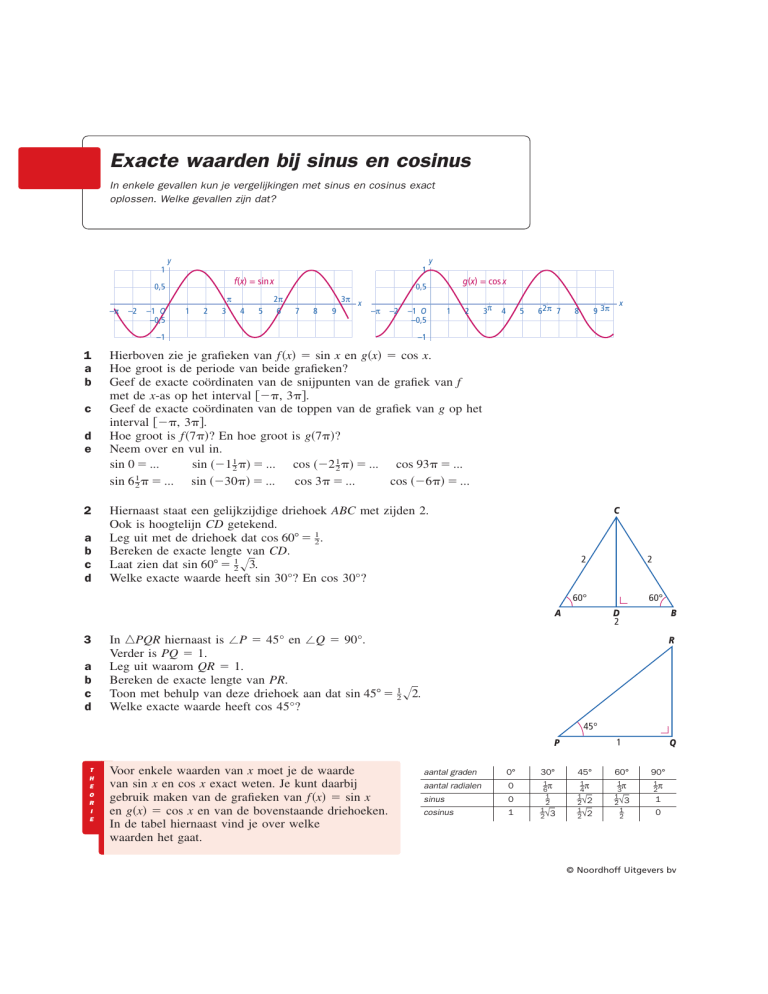
Hierboven zie je grafieken van f 共x兲 ⫽ sin x en g共x兲 ⫽ cos x.
Hoe groot is de periode van beide grafieken?
Geef de exacte coördinaten van de snijpunten van de grafiek van f
met de x-as op het interval 关⫺␲, 3␲兴.
Geef de exacte coördinaten van de toppen van de grafiek van g op het
interval 关⫺␲, 3␲兴.
Hoe groot is f 共7␲兲? En hoe groot is g共7␲兲?
Neem over en vul in.
sin 0 ⫽ ...
sin 共⫺1 21 ␲兲 ⫽ ... cos 共⫺2 21 ␲兲 ⫽ ... cos 93␲ ⫽ ...
1
sin 6 2 ␲ ⫽ ... sin 共⫺30␲兲 ⫽ ...
cos 3␲ ⫽ ...
cos 共⫺6␲兲 ⫽ ...
Hiernaast staat een gelijkzijdige driehoek ABC met zijden 2.
Ook is hoogtelijn CD getekend.
Leg uit met de driehoek dat cos 60⬚ ⫽ 21 .
Bereken de exacte lengte van CD.
Laat zien dat sin 60⬚ ⫽ 21 冪3.
Welke exacte waarde heeft sin 30°? En cos 30°?
C
2
2
60°
A
3
a
b
c
d
60°
D
2
B
In 䉭PQR hiernaast is ⬔P ⫽ 45° en ⬔Q ⫽ 90°.
Verder is PQ ⫽ 1.
Leg uit waarom QR ⫽ 1.
Bereken de exacte lengte van PR.
Toon met behulp van deze driehoek aan dat sin 45⬚ ⫽ 21 冪2.
Welke exacte waarde heeft cos 45°?
R
45°
1
P
T
H
E
O
R
I
E
Voor enkele waarden van x moet je de waarde
van sin x en cos x exact weten. Je kunt daarbij
gebruik maken van de grafieken van f共x兲 ⫽ sin x
en g共x兲 ⫽ cos x en van de bovenstaande driehoeken.
In de tabel hiernaast vind je over welke
waarden het gaat.
Q
aantal graden
0°
30°
45°
60°
90°
aantal radialen
0
1
–π
6
1
–π
3
1
–π
2
sinus
0
1
–
2
–12√3
1
cosinus
1
–12√3
1
–π
4
–12√2
–12√2
1
–
2
0
© Noordhoff Uitgevers bv
4
a
b
c
5
a
b
c
d
A
A
N
P
A
K
Gebruik de grafieken op de vorige bladzijde.
Geef van de volgende vergelijkingen de exacte
oplossingen op het interval 关⫺␲, 3␲兴.
sin x ⫽ 21
d cos x ⫽ 0
sin x ⫽ ⫺ 21
e sin x ⫽ 21 冪2
1
f cos x ⫽ ⫺ 21 冪3
cos x ⫽ 2
Hiernaast staat de grafiek van f共x兲 ⫽ cos 3x op
het interval 关⫺␲, ␲兴.
In deze opdracht ga je de vergelijking cos 3x ⫽ 21 冪3
op het interval 关⫺␲, ␲兴 oplossen.
Voor één oplossing geldt 3x ⫽ 61 ␲. Leg dat uit.
1
Eén oplossing is x ⫽ 61 ␲ ⬊ 3 ⫽ 18
␲.
Welke oplossing volgt dan uit de symmetrie in de
y-as?
Welke periode heeft de grafiek van f?
Gebruik de periode om de overige vier oplossingen
te berekenen.
sin x ⫽ ⫺1
sin x ⫽ 21 冪3
cos x ⫽ ⫺ 21 冪2
g
h
i
y
1
0,5
π
–π
–3
–2
–1
O
1
2
3
4
5
6
7
7
11
1––π
1––π
12
12
–0,5
–1
Hoe los je de vergelijking f(x) = p met f een goniometrische functie en p
een constante, exact op een gegeven interval op?
1 Gebruik de tabel met exacte waarden en zonodig de grafiek om één
oplossing te vinden.
2 Stel de periode van de functie vast.
3 Schets de grafiek van f op het gegeven interval en geef de gevonden
oplossing in de schets aan.
4 Gebruik de periode en de symmetrie van de grafiek om de overige
oplossingen te vinden.
Voorbeeld
1
Los 4 + 3sin 2x = 2–
op het interval [–π, 2π] exact op.
y
2
Oplossing
1 4 + 3sin 2x = 2–1
7
2
6
1
3sin 2x = –1–2
5
sin 2x = – –1
2
4
Met behulp van de tabel en de grafiek:
3
1
1
één oplossing is 2x = – –π
dus x = –––π.
6
12
2
1
2 De periode is 2π : 2 = π.
3 Zie de schets hiernaast.
5
1
of x = – ––π
4 De oplossingen zijn: x = –––π
12
–π
–4
12
7 of x = ––π
11 of x = 1––π
7 of x = 1––π
11
of x = ––π
12
© Noordhoff Uitgevers bv
12
12
12
–3
–2 –1 O
5
1
– ––π
– ––π
12
12
1
–π
4
π
1
2
3
7
11
––π
––π
12
12
2π
x
x
6
a
b
Los de volgende vergelijkingen op het gegeven interval exact op.
2 sin 3x ⫽ 冪3 op 关⫺␲, ␲兴
6 cos 21 x ⫽ 3冪2 op 关0, 3␲兴
7
a
b
c
Gegeven is de functie f共x兲 ⫽ 1 ⫹ sin 共x ⫹ 31 ␲兲.
Teken de grafiek op het interval 关⫺␲, 2␲兴.
Welke periode heeft de grafiek van f?
Bereken met behulp van de periode en de horizontale verschuiving
bij welke waarden van x de symmetrieassen liggen.
Los de vergelijking 1 ⫹ sin 共x ⫹ 31 ␲兲 ⫽ 1 21 op 关⫺␲, 2␲兴 exact op.
d
8
a
b
c
d
e
Hiernaast zie je op het interval 关⫺2␲, 2␲兴 de
grafieken van de functies f共x兲 ⫽ 2x ⭈ sin x en
g共x兲 ⫽ x.
Bereken f 共 61 ␲兲 exact.
Bereken f 共 31 ␲兲 exact.
Om de coördinaten van de snijpunten van beide
grafieken te berekenen, moet je de vergelijking
2x ⭈ sin x ⫽ x oplossen.
Deze vergelijking is gelijkwaardig met
x ⫽ 0 of 2sin x ⫽ 1. Leg dat uit.
Los de vergelijking 2x ⭈ sin x ⫽ x exact op.
Geef de exacte coördinaten van de vijf snijpunten
die hiernaast te zien zijn.
y
5
4
3
f
2
1
–7
–2π
–6 –5
–π
–4 –3 –2
π
–1 O
–1
1
2
3
4
5
6
2π
x
7
–2
g
–3
–4
–5
–6
–7
–8
–9
–10
9
a
b
c
10
a
b
c
d
e
Los de volgende vergelijkingen op het gegeven
interval exact op.
4x ⭈ cos x ⫽ x ⭈ 2冪2 op 关0, 2␲兴
2x 2 ⭈ sin 2x ⫽ x 2冪3 op 关⫺␲, ␲兴
6x ⭈ cos x ⫹ 3x ⫽ 0 op 关9␲, 12␲兴
De grafiek van functie f共x兲 ⫽ 2x ⭈ sin x uit opdracht 8 lijkt
een top te hebben bij x ⫽ 2.
Als de grafiek van f een top heeft bij x ⫽ 2, dan moet f ⬘共2兲 ⫽ 0.
Gebruik de productregel om de afgeleide van f te berekenen.
Bereken f ⬘共2兲 en laat zien dat f ⬘共2兲 ⬎ 0.
Ligt de genoemde top links of rechts van x ⫽ 2?
Ga na dat de exacte waarde van de helling van de grafiek
van f in het punt 共 61 ␲, 61 ␲兲 gelijk is aan 1 ⫹ 61 ␲冪3.
Bereken de exacte waarde van de helling van de grafiek
van f in het punt 共 41 ␲, 41 ␲冪2兲.
© Noordhoff Uitgevers bv
Algemene oplossingen goniometrische
standaardvergelijkingen
Vaak hebben goniometrische vergelijkingen meer dan één oplossing.
Welke?
11
a
b
c
d
T
H
E
O
R
I
E
Gegeven is de functie f共x兲 ⫽ sin x.
Plot de grafiek van f op het interval 关0, 2␲兴.
Geef aan voor welke twee exacte waarden van x op 关0, 2␲兴 geldt dat
sin x ⫽ sin 61 ␲.
Als je de grafiek van f niet beperkt tot het interval 关0, 2␲兴 heeft de
vergelijking sin x ⫽ sin 61 ␲ meer oplossingen. Geef al deze oplossingen.
Bepaal alle exacte oplossingen van de vergelijking cos x ⫽ cos 61 ␲.
De algemene oplossing van de vergelijking sin x ⫽ sin a is:
x ⫽ a ⫹ k ⭈ 2␲ of x ⫽ ␲ ⫺ a ⫹ k ⭈ 2␲, waarbij k elk geheel
getal kan zijn.
De algemene oplossing van de vergelijking cos x ⫽ cos a is:
x ⫽ a ⫹ k ⭈ 2␲ of x ⫽ ⫺a ⫹ k ⭈ 2␲, waarbij k elk geheel getal
kan zijn.
Deze twee vergelijkingen heten goniometrische
standaardvergelijkingen. Andere goniometrische
vergelijkingen kun je vaak tot deze standaardvergelijkingen
herleiden
Voorbeeld
Bereken exact de algemene oplossing van
3
sin 2x = sin –π.
4
Oplossing
3
2x = –π
+ k ⋅ 2π of
4
3
2x = π – –π
+ k ⋅ 2π
4
Delen door 2 en vereenvoudigen geeft
3
1
x = –π
+ k ⋅ π of x = –π
+k⋅π
8
8
Voorbeeld
1
1
Bereken exact de algemene oplossing van cos 1–x
= cos(x – –π).
2
3
Oplossing
1
1
1
1
1–x
= x – –π
+ k ⋅ 2π of 1–x
= –(x – –π)
+ k ⋅ 2π
2
3
2
3
1
1
1
1
= – –π
+ k ⋅ 2π of 1–x
= –x + –π
+ k ⋅ 2π
–x
2
3
2
3
2
1
1
x = – –π + k ⋅ 4π of 2–x = –π + k ⋅ 2π
3
2
3
2
2
x = – –π
+ k ⋅ 4π of 5x = –π
+ k ⋅ 4π
3
3
2
2
4
x = – –π + k ⋅ 4π of x = ––π + k ⋅ –π
3
15
5
12
a
b
c
13a
b
c
Bereken exact de algemene oplossing
sin x ⫽ sin 3x
d
cos 4x ⫽ cos 共 65 ␲ ⫺ x兲
e
f
sin 共2x ⫹ 1 41 ␲兲 ⫽ sin 共x ⫺ 41 ␲兲
van de volgende vergelijkingen.
cos 21 x ⫽ cos 共0,6␲ ⫺ x兲
2 sin 共4x ⫺ 32 ␲兲 ⫽ 冪3
cos 共␲x兲 ⫽ cos 共 51 ␲ ⫺ 21 ␲x兲
Gegeven is dat sin x ⫽ cos 共a ⫺ x兲. Welk getal kan a zijn?
Bereken exact de algemene oplossing van sin x ⫽ cos x.
Bereken exact de algemene oplossing van ⫺sin x ⫽ sin 2x.
© Noordhoff Uitgevers bv
T
H
E
O
R
I
E
Vaak zijn goniometrische formules nodig bij het oplossen van
goniometrische vergelijkingen:
sin x ⫽ cos 共 21 ␲ ⫺ x兲 en cos x ⫽ sin 共 21 ␲ ⫺ x兲, om van sinus naar cosinus
over te gaan of omgekeerd, of om een minteken weg te werken:
⫺sin x ⫽ sin 共⫺x兲 ⫽ sin 共x ⫺ ␲兲 ⫽ sin 共x ⫹ ␲兲
⫺cos x ⫽ cos 共x ⫹ ␲兲 ⫽ cos 共x ⫺ ␲兲 ⫽ cos 共␲ ⫺ x兲
Voorbeeld
2
Los op: –sin(–π
– x) = cos(2x).
3
Oplossing
2
1
sin(– –π
+ x) = sin(–π
– 2x)
3
2
2
1
2
1
– 2x + k ⋅ 2π of – –π
+ x = π – (–π
– 2x) + k ⋅ 2π
– –π
+ x = –π
3
2
3
2
1
2
2
1
3x = –π + –π + k ⋅ 2π of – –π + x = π – –π + 2x + k ⋅ 2π
2
3
3
2
7
2
1
+ k ⋅ 2π of – –π
+ x = –π
+ 2x + k ⋅ 2π
3x = –π
6
3
2
7
2
1
2
x = ––π
+ k ⋅ –π
of –x = –π
+ –π
+ k ⋅ 2π
18
3
2
3
7
2
1
x = ––π
+ k ⋅ –π
of x = –1–π
+ k ⋅ 2π
18
3
6
14
a
b
c
T
H
E
O
R
I
E
Bereken exact de algemene oplossing van de volgende vergelijkingen.
sin 4x ⫽ cos x
d sin 共 21 ␲x兲 ⫽ ⫺cos ␲共x ⫺ 1兲
sin 0,5x ⫽ ⫺cos x
e ⫺2冪2 ⫽ 4 cos 3x
f sin 共2x ⫺ 1 65 ␲兲 ⭈ 共2 cos x ⫺ 1兲 ⫽ 0
cos 共␲ ⫺ x兲 ⫽ ⫺sin 2x
Soms moet je alle oplossingen op een gegeven interval
berekenen. Je berekent dan eerst de algemene oplossing en
gaat vervolgens na welke oplossingen binnen dat interval
liggen.
Voorbeeld
Bereken alle oplossingen op [0, 2π] van de
vergelijking in het voorbeeld hierboven.
Oplossing
7
2
+ k ⋅ –π.
Bekijk eerst x = ––π
18
3
Een oplossing die voldoet is die voor
15
a
b
16
a
b
c
d
Op het interval 关⫺4␲, 3␲兴 is gegeven de functie
f共x兲 ⫽ 2 sin 共 21 x ⫹ 31 ␲兲 ⫺ 1
In welk punt snijdt de grafiek van f de verticale as?
Bereken exact de x-coördinaten van de snijpunten van de
grafiek van f met de x-as.
Bereken exact de oplossingen van de volgende vergelijkingen
op het daarbij aangegeven interval.
sin 7x ⫹ cos 2x ⫽ 0 op 关0, ␲兴
cos 共3x ⫹ 32 ␲兲 ⫺ cos 3x ⫽ 0 op 关⫺ 21 ␲, 21 ␲兴
sin 共␲x兲 ⫽ ⫺cos 共 32 ␲x兲 op 关⫺2, 4兴
sin 41 x ⭈ 共1 ⫺ cos 21 x兲 ⫽ 0 op 关⫺2␲, 4␲兴
© Noordhoff Uitgevers bv
7
k = 0: x = ––π.
18
2
Vanwege k ⋅ –π
liggen andere oplossingen
3
12
2
steeds op een afstand –π
(= ––π),
zodat je
18
3
7
12
1
krijgt x = ––π
+ ––π
= 1––π
en
18
18
18
13
19
12
31
x = ––π + ––π = ––π = 1––π.
18
18
18
18
1
Bekijk nu x = –1–π
+ k ⋅ 2π, dan geeft
6
k = 1 de enige oplossing:
5
x = –π.
6