Audiologie → Geluid

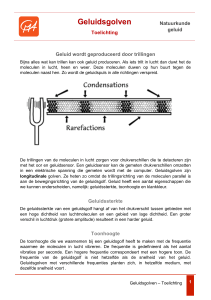
Audiologie  Geluid
Inleiding
Voor ons als goedhorenden is het horen van geluiden en het verstaan van stemmen de meest
logische zaak van de wereld. Pas als je na gaat denken over geluid, ga je je realiseren dat geluid een
lastig fenomeen is om te beschrijven.
Als we de zee horen, dan zeggen we dat de zee ruist. Maar probeert u nou eens te vertellen wat ruis
is; zonder het na te doen; zonder het met uw mond te reproduceren, waardoor u een voorbeeld
geeft hoe het klinkt. Dat is enorm moeilijk en dan hebben we het nog maar over geluid met een vrij
constante luidheid en een vrij monotoon karakter.
Het beschrijven van het geluid van een blaffende hond wordt al een stuk lastiger. Het geluid is
wisselend van karakter, van toon en van luidheid. Als je goed luistert kun je min of meer de
stemming van de hond herkennen aan zijn geblaf.
Een van de meest moeilijke geluiden om te beschrijven is spraak of gesproken woord. Dat komt
omdat er niet alleen een enorm scala van klanken aan te pas komt, maar ook van klemtonen, en
verschillende betekenissen van woorden en ook de zinsopbouw kan heel anders zijn, terwijl toch
hetzelfde bedoeld wordt.
Probeert u maar eens uit op hoeveel manieren u de volgende zin kunt uitspreken, opdat hij ook een
wezenlijk andere betekenis krijgt
Heb jij het wel eens gedaan?
Kortom reden genoeg om geluid eens wat nader onder de loep te nemen en te kijken hoe het wordt
geproduceerd en wat we er mee kunnen om het te analyseren.
Zuivere tonen verses gewone geluiden.
De dagelijkse geluiden om ons heen zijn complex van aard. Daar bedoelen we mee dat we eigenlijk
nooit één ding tegelijk horen, maar een heleboel klanken tegelijk. Om zo’n geluid beter te kunnen
begrijpen zou je het eerst moeten opdelen in een groot aantal componenten die, als je al die
geluiden tegelijk zou laten horen, samen de bedoelde klank zouden maken. Als je al die
componenten uit elkaar hebt getrokken, zou je component voor component onder de loep kunnen
nemen om de specifieke eigenschappen te onderzoeken. Voor ons niveau gaat dat wat ver en
daarom nemen we ter bestudering van geluid voorlopig alleen de zogenaamde zuivere tonen. Tonen
die slechts uit één component bestaan. Dit soort geluiden vind je bijvoorbeeld terug in
snaarinstrumenten of in een stemvork. De geluiden die hiermee worden opgewekt noemen we
zuivere tonen, alle andere geluiden die niet zuiver zijn en dus opgebouwd uit meerdere
componenten noemen we complexe geluiden of complexe tonen
1
Het ontstaan van geluid
Als we een elastiekje tussen twee punten spannen (bijvoorbeeld onze vingers), dan kunnen we de
ontstane snaar in trilling brengen door hem uit te rekken en plotseling los te laten. De snaar zwiept
nu naar zijn neutrale (oorspronkelijke) stand terug, maar in zijn vaart schiet hij dit punt voorbij totdat
hij weer uitgerekt is en onder spanning staand tot de ontdekking is gekomen dat hij is
doorgeschoten. Hierop gaat hij weer terug en schiet opnieuw zijn doel voorbij. Kortom het elastiekje
staat te trillen en die trilling wordt steeds zwakker totdat de ruststand is bereikt en de snaar weer stil
staat.
Dit experiment kun je doen met een elastiekje, maar je kunt het ook doen met bijvoorbeeld een
gitaarsnaar. De aangeslagen snaar gaat trillen in een bepaald aantal trillingen per seconde waar hij
zich lekker bij thuis voelt. Welke toon dat is, hangt af van het materiaal waarvan de snaar gemaakt is
en de lengte van de snaar.
Lange slap gespannen snaren trillen langzaam, korte strak gespannen snaren trillen snel.
Figuur 1
Een harp kent korte en lange snaren
Iedere keer als de snaar door de lucht gaat, brengt hij luchtmoleculen in beweging. Op de heenweg
drukt hij de luchtmoleculen naar voren, op de terugweg zuigt hij ze als het ware weer achter zich
aan. Deze luchtmoleculen brengen uiteraard ook elkaar in trilling. Ze drukken elkaar vooruit of
trekken elkaar weer terug. Je zou dat proces kunnen vergelijken met een menigte mensen voor een
podium. Als de voorste mensen een meter achteruit geduwd worden, komt de hele mensenmassa in
beweging. De tweede rij mensen gaat geen hele meter achteruit, maar bijvoorbeeld maar 95 cm, de
derde rij 90, de vierde rij 85 enz, enz.
De één na laatste rij met mensen hebben slechts de neiging iets te bewegen zonder echt van plaats
te veranderen. De mensen op de allerlaatste rij van de zaal kunnen simpelweg niet achteruit doordat
ze tegen de muur staan en komen dus in het geheel niet meer in beweging. Op een gelijke manier
plant geluid zich voort door de ruimte. De luchtmoleculen botsen op elkaar maar naarmate de
botsingen verder van de bron zijn neemt de kracht af en sterft het geluid uit.
Het verschil met de mensenmassa is dat de luchtmoleculen zich niet netjes aan de twee dimensies
van het vloeroppervlak houden, maar ook de derde dimensie gebruiken t.w. de hoogte, waardoor
het verhaal net iets ingewikkelder wordt.
Voortplantingssnelheid
Hoe we de lucht ook in trilling brengen, met een snaar, of met een luidspreker, met een gong, met
een fluit of met een stem, de voortplantingssnelheid van dat geluid door de lucht gaat altijd even
snel. De voortplantingssnelheid van geluid door de lucht is enigszins afhankelijk van de luchtdruk en
2
de luchtvochtigheid, maar gemiddeld gaat geluid met een snelheid van 330 – 340 meter per seconde
door de lucht. Als je dat omrekent kom je op zo’n 1200 km per uur uit.
Kijk je vanaf enige afstand naar een heimachine, dan hoor je de klap van het blok enige tijd nadat je
het blok hebt zien landen. Het geluid had tijd nodig om jou te bereiken.
Zie je een vliegmachine op een paar kilometer hoogte, dan lijkt het geluid zich erachter te bevinden.
Het geluid heeft tijd nodig om de aarde te bereiken en op het moment dat het geluid is aangekomen
is het vliegtuig al weer een stuk doorgevlogen.
Soms zonder het te weten gebruiken mensen de rekenwijze die daarbij hoort. Ze kijken naar een
onweersbui, zien een bliksemschicht, en tellen hardop het aantal seconden dat verstrijkt voordat ze
de donder horen. De meeste mensen zeggen dan: Voor iedere 3 tellen (seconden) rekenen we één
kilometer. Horen we dus 9 tellen later de donder dan rekenen we snel uit dat de bui ongeveer 9 / 3 =
3 km van ons verwijderd is. (3 x 330 m = 990 m = 1 km)
In feite wordt gebruik gemaakt van de formule
S= V x T
S= De afgelegde weg V= de voortplantingssnelheid van het geluid T = de tijd in seconden
3000 m = 330 m per seconde x
9 seconden
Niet alleen in lucht wordt het geluid doorgegeven. Ook andere materialen geleiden geluiden. Als u
wel eens in een haven gezwommen heeft, weet u dat u vaak een boot onder water al hoort
aankomen, terwijl je boven water nog niets verneemt.
Een ander voorbeeld is het boren van een gat in beton dat door alle woningen van het flatgebouw te
horen is alsof de boor ieder moment bij u uit de wand kan komen.
Dit soort geluiden die voortkomen uit geluiden die in belendende panden worden geproduceerd,
noemen we overigens contactgeluiden. Het geluid wordt door de muren geleid en bereikt op die
manier uw woning.
Als in een blok rijtjeshuizen op de ene hoek een schaal op de plavuizen aan diggelen gaat, kan dat
met gemak in het hele blok gehoord worden. Ook dat is contactgeluid.
Ook het bekende grapje van de indiaan die om onbegrijpelijke reden telkens weer zijn hoofd op de
spoorrails legt om te horen of er een trein aan komt (om daarna over te steken?) illustreert ons dat
geluid in metalen op een prima manier geleid wordt. Dit komt doordat de staalmoleculen heel dicht
tegen elkaar zitten. Als de voorste (onder de wielen van de trein) in beweging worden gezet, moeten
de achtersten (onder het oor van de indiaan) wel mee bewegen. De voortplantingssnelheid in
metalen is dan ook bijzonder hoog.
We maken dagelijks veel sommetjes die te maken hebben met de voortplantingssnelheid van geluid.
Onlangs stond in de Quest-special nr. 3 een artikel dat eveneens met dit onderwerp te maken heeft
en mijn verbazing wekte. Zie Figuur 2
3
Figuur 2
De snelheid van het geluid in de sport
In praktijk hebben audiciens vrijwel uitsluitend met voortplanting van geluid door de lucht te maken.
Een uitzondering daarop vormen contactgeluiden die wel eens storing geven in de geluidsarme
ruimte waarin gehoortesten worden afgenomen. Geluiden veroorzaakt door buren of machines in en
rond het pand kunnen hier bijzonder storend bij zijn.
Toonhoogte
Bepalend voor de toonhoogte van een geluid is hoe vaak de moleculen in de lucht van voren naar
achteren worden geslingerd, ofwel hoeveel keren de luchtdruk groter en kleiner wordt.
Een trillende snaar varieert telkens van positie in de lucht. Hij beweegt daarbij om zijn neutrale
stand, de stand waarin hij verkeert als hij stil staat. Voor (maar ook achter) de snaar ontstaan dus
luchtdruk verschillen die ons oor kan waarnemen in de vorm van geluid.
4
Proberen we het proces van een trillende snaar zichtbaar te maken dan ontstaat de illustratie uit
Figuur 3.
Figuur 3
De uitwijking van een snaar en de daarbij optredende luchtdrukvariaties
We zien de tijdas horizontaal uitgezet op de x-as en zien de luchtdruk variaties op de verticale as (de
y-as) uitgezet. Als de snaar begint te trillen zal de luchtdruk iets toenemen tot de snaar in de uiterste
stand is gekomen (A), daarna zal de snaar terugveren waardoor de luchtdruk minder wordt. Schiet de
snaar door de neutrale stand (B), dan ontstaat een onderdruk, doordat de snaar de lucht als het ware
achter zich aan zuigt. Als weer de uiterste stand bereikt is (C) gaat de snaar terug en de druk loopt
weer op. Als opnieuw de neutrale stand wordt bereikt (D) herhaalt zich het proces.
De tijd die nodig is om één trilling te doorlopen noemen we een periode. Het golf model dat de druk
weergeeft middels de rode lijn, heet een sinus. We praten dan over een trilling zoals weergegeven in
onderstaande Figuur 4
Figuur 4
Een sinus met aangegeven één periode
Van een snaar weten we dat een korte snaar sneller trilt dan een lange. Ook een snaar die strakker
gespannen staat heeft de neiging om sneller te trillen.
Daarbij kunnen we constateren dat hoe sneller de snaar trilt hoe hoger de toon is die we horen. Dus
een lange snaar die slap gespannen staat geeft dus een laag geluid (denk aan een contrabas) en een
korte snaar die strak gespannen staat geeft een hoog geluid (denk aan de ukelele). Een ander
instrument dat deze theorie mooi illustreert is de harp of de vleugel. Hoe langer de snaar hoe
donkerder de toon en omgekeerd hoe korter de snaar hoe hoger de toon. Door de spanning in de
snaar te variëren wordt het muziekinstrument gestemd.
Een leuk hulpmiddeltje om deze theorie te kunnen onthouden is een zakkammetje met tanden van
verschillende lengte. Als we met een nagel langs de tanden van het kammetje strijken, krijgen we
5
een aantal geluidjes te horen, die steeds hoger van klank worden naarmate we langs kortere tanden
strijken.
Als u op die manier voorwerpen gaat bekijken zult u merken dat u veel muziekinstrumenten kunt
maken van alledaagse voorwerpen. Want we zoeken het nu alsmaar in min of meer gesnaarde
instrumenten, maar ook bijvoorbeeld een trommel werkt op het zelfde principe. Als we een heel
klein trommeltje nemen, waarvan het vel strak gespannen staat, krijgen we een scherp en hoog
geluid. Nemen we daarentegen een grote trommel met een veel slapper membraan, dan klinkt het
geluid veel donkerder. Kijk in de kast naar potten en pannen en u kunt volop experimenteren.
Gaan we het fenomeen toonhoogte grafisch weergeven dan ontstaat Figuur 5.
Hier zien we twee trillingen boven elkaar weergegeven. U ziet dat het aantal trillingen (het aantal
periodes) van het tweede geluid in dezelfde tijd groter is dan van het eerste geluid. Om precies te
zijn, zijn er twee keer zoveel trillingen in dezelfde tijd.
Figuur 5
Toonhoogte: De onderste toon is twee keer zo hoog als de bovenste
Het aantal trillingen per seconde bepaalt de toonhoogte van een geluid. Een ander woord voor het
aantal trillingen per seconde waarmee het geluid is opgebouwd, is de frequentie van het geluid.
Deze frequentie wordt uitgedrukt in de eenheid Hertz (Hz).
Een veelvoorkomende toonhoogte, die we bijvoorbeeld ook op de audiometer terugvinden, heeft
een frequentie van 1000 Hz. Dat wil zeggen dat de geluidsdruk 1000 keer per seconde varieert. Een
toon van 2000 Hz heeft 2 x zoveel sinussen en klinkt 2 x zo hoog. Ons oor kan ogenblikkelijk
vaststellen of we te maken hebben met een hele hoge of juist een lage toon.
Als we tonen qua klank met elkaar vergelijken en we vergelijken een basistoon met tonen die 2, 3 of
4 keer zo hoog zijn, horen we meteen dat ze mooi t.o.v. elkaar klinken. Ze zijn in harmonie met
elkaar. De basistoon met de laagste frequentie noemen we de grondtoon of de eerste harmonische.
De toon die twee keer zoveel trillingen kent is de 2de harmonische. De toon die drie keer zo hoog is
de 3de harmonische, enzovoort.
6
Nemen we een grondtoon van 500 Hz, dan is de tweede harmonische 1000 Hz. De derde
harmonische is dan 1500 Hz, de vierde 2000 Hz, enzovoort.
Als je al die tonen tegelijk laat horen, dan klinken ze mooi en horen ze bij elkaar. We zeggen dan,
bijvoorbeeld bij een muziekinstrument, dat ze goed gestemd zijn.
Laten we daarentegen een toon van 1000 Hz en een toon van 2100 Hz tegelijk horen, dan horen we
meteen dat die tonen vals klinken t.o.v. elkaar. Ze horen niet bij elkaar.
Het leuke is dat ons oor kennelijk heel goed in staat is om te bepalen wat zuiver klinkt (wat in
harmonie is met elkaar) en wat vals klinkt (disharmonie). Sterker nog ons oor is in staat in de lage
tonen, en dan spreken we over tonen van minder dan 500 Hz, verschillen of fouten van minder dan
2 Hz te kunnen horen. Boven de 500 Hz is ons oor iets minder selectief en kunnen we “slechts” 0.3%
van de frequentie als verschil of fout herkennen. Bij een toon van 1000 Hz is dit dus 3 Hz en bij 8000
Hz, de hoogste toon op de audiometer, is het benodigde verschil nog slechts 24 Hz. We praten
daarbij, zo u zult begrijpen, over een gezond en onbeschadigd oor.
De Golflengte
We weten dat de voortplantingssnelheid van geluid ongeveer 330 meter per seconde bedraagt. We
weten ook dat je de toonhoogte van een geluid uitdrukt in het aantal trillingen per seconde, ofwel de
frequentie. Nemen we een toon van 1000 Hz, dan wil dat zeggen dat er 1000 trillingen per seconde
plaatsvinden. In die ene seconde werd door het geluid een afstand afgelegd van 330 meter. Delen we
de afgelegde weg door het aantal trillingen, dan weten we van iedere golf hoe lang die geweest moet
zijn. In ons voorbeeld 330 meter / 1000 trillingen = 0,33 m per trilling ofwel 33 cm.
Deze waarde noemen we de golflengte van het geluid.
Figuur 6
Naarmate de frequentie toeneemt, neemt de golflengte af
7
Een trilling die een lage frequentie heeft (een lage toon van bijvoorbeeld 100 Hz) heeft een lange
golflengte van 330 m / 100 = 3,3 m of 330 cm
Een hoge frequentie (bijvoorbeeld 8000 Hz) heeft een hele korte golflengte want 330 / 8000=
0,04125 m ofwel 4,125 cm = ±4 cm
De golflengte wordt aangeduid met de Griekse letter λ (labda). In het laatste voorbeeld was λ dus
gelijk aan 4cm.
Kijken we ter illustratie nog even naar Figuur 6 dan zien we dat wanneer de frequentie twee keer zo
groot is geworden, de golflengte de helft is. Maken we de toon drie keer zo hoog, dan wordt de
golflengte 3 x zo klein. Het onderste voorbeeld laat zien dat als we de frequentie 12 x zo groot
maken, de golflengte 12 x zo klein wordt. Ofwel 4 cm / 12 = 0.33 cm
De luidheid van een geluid
Als we weer terug gaan naar onze gitaarsnaar of ons elastiekje, dan is het heel makkelijk te
constateren dat als je de snaar verder uittrekt voor je hem loslaat, het geluid dat geproduceerd
wordt harder gaat klinken. Hieruit kunnen we concluderen: Hoe groter de uitwijking van de snaar,
hoe harder het geluid. En omgekeerd hoe minder ver de snaar wordt uitgetrokken, hoe zachter het
geluid is.
We kijken nog steeds naar de ons bekende sinus uit Figuur 3 en plaatsen deze nu bovenin Figuur 7
De slingerende beweging heeft een bepaalde uitwijking t.o.v. zijn neutrale stand. Deze uitwijking
noemen we de amplitude.
Figuur 7
Variatie van luidheid (de amplitude) van het geluid
8
Als we de snaar verder uittrekken en loslaten, wordt de uitwijking van de snaar groter; ofwel de
amplitude van de sinus wordt groter, wat tevens tot gevolg heeft dat het geluid harder wordt.
Dus hoe groter de uitwijking van de sinus, des te groter is de luidheid en omgekeerd geeft een kleine
uitwijking slechts weinig geluid.
Resumé:
We kennen zuivere tonen en complexe signalen
Een zuivere toon wordt ook wel een sinusvorm genoemd
De toonhoogte van een geluid wordt uitgedrukt in het aantal trillingen per seconde
De toonhoogte wordt ook wel de frequentie genoemd en aangeduid met de letter F.
De frequentie wordt uitgedrukt in het aantal trillingen per seconde ofwel het aantal Hertz (Hz)
Een periode of golflengte van het geluid beslaat de tijd die nodig is om een volledige trilling te
doorlopen.
De golflengte wordt uitgedrukt in meters of centimeters en wordt aangeduid met de letter λ
De uitslag van de trilling heet de amplitude
Hoe groter de amplitude hoe harder het geluid.
Hoe kleiner de amplitude hoe zachter het geluid
Geluidsdruk
In de vorige hoofdstukken heeft u kunnen lezen dat geluid eigenlijk kleine luchtdrukverschilletjes zijn
die ons trommelvlies in beweging zetten. Die drukverschilletjes zijn ongelofelijk klein en het mag een
wonder wezen dat ons trommelvlies zo gevoelig is dat deze opgevangen kunnen worden.
Als we in de techniek druk willen meten, gebruiken we daar, als het om hele hoge druk gaat, een
manometer voor. We meten dan in de eenheid “atmosfeer” of ”bar”. Als de druk die we willen
meten kleiner wordt, gebruiken we bijvoorbeeld een barometer. Deze meet de luchtdruk om ons
heen in duizendsten van een Bar nauwkeurig. (0.001 Bar = 1 milliBar = 1 mBar = 10-3 Bar).
Om nog kleinere luchtdrukverschillen te kunnen meten is zelfs de milliBar nog een te grote eenheid.
Om een kleinere eenheid te hebben, bedacht meneer Pascal ooit “de Pascal” afgekort Pa.
1 Pa is 1/100 mBar
of 0.01 milliBar of 0,00001 Bar of
10-5 Bar.
Voor het doel om geluidsdruk te meten is zelfs de Pascal nog veel te groot en daarom drukt men de
1
geluidsdruk van geluid uit in micro Pascal’s (μ Pa). Dat is 0,000.001 Pascal en dus
/1000.000
deel van een Pascal.
1 pascal was 1/100 mBar dus 1 mBar = 100.000.000 μ Pa
hieruit volgt 1 Bar = 100.000.000.000 μ Pa of 1 Bar = 10 11 μ Pa
Gehoordrempel
Met deze kennis heeft men uiteindelijk uitgevonden dat het gemiddelde menselijk oor een geluid
met een toonhoogte van 1000 Hz bij een geluidsdruk van 20 μPa nog net kan horen.
Betekent dat nou dat als de geluidsdruk kleiner is dan 20 μPa dat er dan geen geluid meer is? Neen,
er is dan nog steeds geluid, alleen wij (de mens) kunnen het met onze oren niet meer horen. Het is
best mogelijk dat een hond of een kat dat geluid nog prima kan waarnemen.
Overigens heeft ons oor niet voor iedere toonhoogte dezelfde gevoeligheid. Als we de toon heel laag
maken, dan is er veel meer geluidsdruk nodig om de toon hoorbaar te maken dan voor de toon van
9
1000 Hz. Ook de hele hoge tonen kunnen door ons oor slechter worden gehoord; er is voor deze
toonhoogten ook een hogere geluidsdruk nodig dan die 20 μPa geluidsdruk waarmee we bij 1000 Hz
de toon nog net konden waarnemen. Er is daarentegen ook een klein stukje in de frequentieband die
we iets beter kunnen horen dan die toon bij 1000 Hz en dat stukje ligt rond de 3000 - 4000 Hz.
Pijndrempel
Om het geluid zo hard te maken dat het ons oor pijn doet, moet je de geluidsdruk opvoeren tot zo’n
20.000.000 μPa of 20 Pa. De geluidsdruk is dan dus bij benadering een miljoen keer (1.000.0000 x) zo
groot als bij de gehoordrempel.
Ook om de pijngrens van ons oor te bereiken, heb je bij de ene toonhoogte een grotere geluidsdruk
nodig dan bij de andere toon. Ons oor is het minst gevoelig voor harde geluiden in de lage en hoge
tonen.
De decibel of dB
Omdat al die nullen en komma’s niet zo lekker gemakkelijk rekenen, heeft men ervoor gekozen de
materie wat eenvoudiger te maken en heeft men besloten om in het vervolg alles om te rekenen
naar dB’s. Dat terugrekenen naar dB’s gaat met logaritmen, een soort verhoudingsgetal. In het kader
van deze lesstof is het echter niet raadzaam om hier verder over uit te wijden, wij redeneren vanaf
hier gewoon verder met decibellen en weten in ons achterhoofd dat we het eigenlijk over de
verhouding van de geluidsdruk t.o.v. de gehoordrempel bij 1000 Hz hebben ofwel die 20 μPa.
Fletcher - Munson curve
Het waren de heren Fletcher en Munson die jaren geleden de gevoeligheid van het oor in kaart
hebben gebracht. Ze deden dat door een groep van 15 jongens en 15 meisjes van ± 13 jaar oud te
selecteren op een gezond gehoor. Met deze kinderen werd per toonhoogte steeds de gevoeligheid
van het oor bepaald. Uiteindelijk werd de gemiddelde gevoeligheid per toonhoogte vastgesteld en
dat leidde tot een grafiek zoals te zien is in Figuur 8
Op de horizontale as werd de toonhoogte uitgezet, de frequentie in Hz. Op de verticale as werd de
geluidsdruk uitgedrukt in dB’s weergegeven. Het uitgangspunt ligt bij 1000 Hz en 0 dB (20 μPa ) en
we kunnen constateren dat er meer druk nodig is om de lage en de hoge tonen te kunnen horen. Bij
4000 Hz zien we dat er juist minder druk nodig is.
10
Figuur 8
Een aantal meetpunten van de Fletcher - Munson curve ter bepaling van de gehoordrempel
In werkelijkheid werden er nog veel meer punten gemeten en uiteindelijk wisten de heren een
grafiek te produceren dat de gehoordrempel op een zeer nauwkeurige manier beschreef.
Deze grafiek kunt u vinden in Figuur 9
Figuur 9
De gehoordrempel
11
De pijn grens
Het hierboven beschreven experiment werd herhaald, maar nu niet om de gehoordrempel vast te
stellen, maar om te kijken hoe hard men het geluid kon maken voordat de kinderen het geluid als
pijn gingen ervaren.
Ook deze resultaten werden aanvankelijk puntsgewijs ingetekend, waarna een soort grafiek ontstond
zoals weergegeven in Figuur 10
Figuur 10
De meetpunten van de pijndrempel
Uiteindelijk werden deze metingen ook bij zoveel punten herhaald, dat het mogelijk was om al die
punten met elkaar te verbinden waardoor een lijn ontstond. Dit figuur vinden we terug in Figuur 11.
De gevonden lijn noemen we de pijndrempel.
12
Figuur 11
De pijndrempel
Het oorspan
Liggen in Figuur 11 de geluiden boven de gehoordrempel, dan zijn ze hoorbaar. Harde geluiden die
aan de bovenkant van de grafiek de pijngrens benaderen zijn onaangenaam om te horen. Alle
geluiden die wij dagelijks horen liggen daar ergens tussenin. Het gebied tussen de hoordrempel en de
pijndrempel noemen we het oorspan.
Uit al deze metingen is vast komen te staan dat mensen met een gezond gehoor tonen kunnen horen
vanaf zo’n 20 Hz. Er is dan wel veel geluidsenergie nodig, maar je kunt ze horen. In het hoog, kunnen
mensen geluiden horen tot zo’n 20.000 Hz. Dat wil zeggen tot ze een jaar of 20 zijn en niet te vaak
naar de disco zijn geweest. Vanaf die leeftijd loopt de hoorbare frequentie in het hoog namelijk
zachtjes aan terug. Bij de één gaat dat langzaam en bij de ander gaat het razend snel. Gelukkig
hebben we die hele hoge tonen voor het verstaan van spraak niet zo hard nodig. Wel voor het
luisteren naar muziek en ook veel geluiden in de natuur bevatten deze hoge geluiden..
Dieren kunnen zachtere geluiden horen die voor een mens onhoorbaar zijn. Ook kunnen ze veel
hogere tonen horen dan mensen. Er zijn dieren die tot wel 50.000 Hz kunnen waarnemen. Een kat
kan bijvoorbeeld heel hoog horen om muizen te kunnen horen die ook heel hoog piepen.
Doordat jonge mensen hoge tonen beter horen dan volwassenen, wordt er tegenwoordig gebruik
gemaakt van “de Mosquito” om hangjongeren te verjagen. Dit apparaat produceert een harde toon
van meer dan 20.000 Hz. De jongeren die hieraan bloot gesteld worden staan met hun handen voor
hun oren, terwijl ouderen in het geheel niets horen. Hoe legaal deze toepassing is, staat overigens
steeds meer ter discussie.
13
Het spraakgebied
Ook gesproken woord, met al zijn klanken en toonhoogtes valt binnen het oorspan. De toonhoogtes
die we in spraak terugvinden liggen grofweg tussen de 100 Hz en de 6000 Hz. Voorbeeld van een hele
lage klank is bijvoorbeeld de ooo en voorbeeld van een hele hoge toon is bijvoorbeeld de ssss of de
vvv. Ook de geluidsintensiteit varieert enorm. Als we tegen elkaar fluiteren heeft dat geluid een
sterkte van 30 – 35 dB en als we in een boze bui tegen elkaar schreeuwen kunnen we de 80 – 90 dB
makkelijk halen.
Dit gebied van spraakklanken wordt weergegeven middels het ovaal in Figuur 12. Dit gebied wordt
het spraakgebied, het spraakovaal of ook wel eens oneerbiedig de spraakbanaan genoemd.
Figuur 12
De gehoordrempel, de pijndrempel met daartussen het oorspan. In het oorspan vinden we het spraakgebied
Isofonen
Wat Fletcher en Munson gedaan hebben voor de gehoordrempel en pijndrempel, kun je natuurlijk
doen voor iedere gewenste geluidsterkte. Je neemt het geluid behorende bij 1000 Hz en 50 dB en
vraagt aan de proefpersonen of hij kan aangeven wanneer een toon van 2000 Hz als precies even luid
ervaren wordt. Vervolgens herhaal je de vraag voor 4000 Hz en voor 8000 Hz. Op die manier vind je
een lijn van geluidsintensiteiten en frequenties waarvan de proefpersoon zegt dat ze allemaal een
gelijke luidheidsensatie teweeg brengen.
Zo’n lijn noemen we een isofoon. Uiteraard kun je dat weer voor een hoop geluidsterktes doen en
omdat ze een hoop subsidie kenden hebben ze al die testen dus ook echt uitgevoerd. Al die lijnen
van gelijke luidheid, al die isofonen, staan getekend in Figuur 13.
14
Figuur 13
Isofonen
Spraakverstaan
Wij zijn in staat om middels spraak te communiceren. Op zich lijkt dat niets bijzonders, maar zodra
iemand in een vreemde taal begint te spreken, begrijpen we er niets meer van. De spreker maakt
geluiden die we niet herkennen en de bedoeling ervan niet begrijpen.
Hieruit blijkt dat horen één is, verstaan twee en begrijpen drie.
Horen doen we met ons geleidingsdeel van het oor, verstaan wordt voor een groot deel
bewerkstelligd in de cochlea of het slakkenhuis en begrijpen doen we met onze hersenen.
We hebben gezien in Figuur 12 dat spraak toonhoogtes kan bevatten tussen de 100 en 6000 Hz.
Daarnaast kunnen er intensiteitverschillen optreden van meer dan 50 dB. En eerder hebben we al
gesproken over het leggen van klemtonen op woorden en zinsdelen, die plotseling een hele andere
betekenis aan spraak kunnen geven dan dat je zou denken als je die informatie niet tot je beschikking
hebt.
Bij een hoop slechthorenden is er niet alleen sprake van zachter horen, maar ook van het
bijvoorbeeld onevenredig slecht horen van de hoge tonen, waardoor een groot deel van de
informatie uit die hoge tonen domweg niet aankomt.
Omdat spraak zo ontzettend gecompliceerd is qua samenstelling is het voor iemand die een deel van
zijn gehoorvermogen mist, vaak erg moeilijk te volgen. Als er dan ook nog eens omgevingsgeluiden
zijn, wordt het voor een slechthorende vaak een brij van geluid waar nog maar weinig
spraakinformatie uit op te halen is.
Het domweg versterken van het geluid is in die situatie geen oplossing. Niet alleen de bruikbare
informatie wordt versterkt, ook de geluiden die de slechthorende veel liever niet zou horen, worden
15
harder gemaakt. Tegenwoordig zijn er hoortoestellen die door toegepaste techniek in staat zijn
spraak beter of meer te versterken dan omgevingsgeluiden. We mogen daar echter niet al te veel van
verwachten. Het zijn allemaal nog technieken die in de kinderschoenen staan.
Gehoorverlies
Als iemand slecht hoort, is zijn eigen 0-isofoon of gehoordrempel verschoven t.o.v. de 0-isofoon van
de goedhorende van de Fletcher Munson curve. We kunnen een test met hem doen en zijn gehoor
vergelijken t.o.v. de 0-isofoon, ofwel de gehoordrempel van een goedhorende. De vraag is dan dus,
hoeveel geluidsdruk moeten we aanbieden om hem een geluid nog net te kunnen laten horen.
Uit de bolletjeslijn (gehoorverlies rechts) in Figuur 14 blijkt dat deze slechthorende een
gehoorverlies heeft t.o.v. een goedhorende van 20 dB bij 250Hz oplopend tot 55 dB bij 8000 Hz.
Figuur 14
Gehoorverlies ingetekend in een Fletcher Munson curve
Lekker handig is dat bepaald niet, omdat je een vergelijking moet maken met een gebogen lijn en de
twee lijnen eerst van elkaar moet aftrekken om tot een gehoorverlies te komen.
Om die reden heeft men in Figuur 15 de 0-isofoon uit de Fletcher Munson curve recht getrokken,
hetgeen al een stuk makkelijker rekent. Daarnaast heeft men geredeneerd dat we een
gehoorVERLIES willen uitdrukken. Dat betekent dat het gehoorverlies dat we willen vergelijken met
de 0-lijn naar alle waarschijnlijkheid slechter is dan die 0-lijn. Visueel is het dan beter de schaal om te
draaien, zodat het gevonden verlies omlaag wordt uitgezet.
16
Figuur 15
De basisvorm van een audiogram
Met de gegevens uit Figuur 14 in ons achterhoofd is een audiogram ontstaan zoals u kunt
terugvinden in Figuur 16
dB’s HL en dB’s SPL
We moeten ons echter wel bedenken dat de dB’s gehoorverlies die we uitbeelden, niets meer te
maken hebben met een geluidsdruk, maar dat we praten over een gehoorverlies t.o.v. het gehoor
van een gemiddelde goedhorende. Om die reden praten we over dB’s Hearing Loss of dB’s HL. Dit in
tegenstelling tot de dB’s waar we het tot nu toe over hebben gehad, want die waren telkens
gerelateerd aan de luchtdruk van 20 μPa zijnde 0 dB. Die dB’s worden uitgedrukt als dB’s SPL of dB’s
Sound Preasure Level (geluids druk niveau).
Kijken we naar Figuur 16 dan zien we dat in dit audiogram het zelfde gehoorverlies getoond wordt als
in Figuur 14, de ernst van de slechthorendheid is hier echter veel sneller in te schatten. Daarnaast is
het ook mogelijk om een betere vergelijking te maken van het gehoorverlies bij verschillende
frequenties. Zo zien we dat we te maken hebben met een oplopend gehoorverlies in de hoge tonen,
terwijl dat in Figuur 14 haast niet te zien was, en al helemaal niet als we de pijlen er niet ingezet
hadden.
17
Figuur 16
Het audiogram met het gehoorverlies uit Figuur 13
In Figuur 16 zien we het gevonden gehoorverlies van boven naar beneden uitgezet. De 0-lijn verbeeldt
eigenlijk de 0-isofoon ofwel het gehoor van de gemiddelde goedhorende. Hoe verder we in het
diagram naar onderen gaan, des te slechter is het gehoor van de cliënt. In dit geval hebben we te
maken met een licht tot middelmatig gehoorverlies dat oploopt in de hoge tonen. De frequentieschaal
is nog steeds logaritmisch hoewel de schaalverdeling er thans veel eenvoudiger uitziet.
Bij sommige cliënten, bijvoorbeeld kinderen met een nog goed gehoor, zou het voor kunnen komen
dat zij zelfs beter horen dan 0 dB. Immers dat was het gemiddelde van al die kinderen en daar zaten
slechte, maar ook goede resultaten tussen. Om die reden bestaat de mogelijkheid om ook
“gehoorverliezen” kleiner dan 0 dB in te vullen. Deze komen dan boven de 0-lijn te staan.
Resumé
Geluidsdruk wordt uitgedrukt in micro Pascal (μPa)
De gevoeligheid van het menselijk oor bij een toon van 1000 Hz is 20 μPa
Het menselijk oor is voor lage tonen en hoge tonen minder gevoelig dan voor de midden tonen
M.b.v. experimenten met kinderen is door Fletcher en Munson de gemiddelde gehoordrempel
bepaald.
Ook is tijdens die experimenten bepaald waar de pijndrempel zich bevindt.
Geluiden harder dan de gehoordrempel en zachter dan de pijndrempel vallen binnen het oorspan
Midden in het oorspan ligt het spraakgebied of de spraakbanaan
Spraak bevat geluiden die in toonhoogte varieren van 100 tot 6000 Hz
Spraak bevat geluiden die in sterkte varieren tussen de 30 en 80 dB
Geluidsvolumes die op alle frequenties een gelijke luidheid teweeg brengen noemen we isofonen
Gehoorverliezen worden genoteerd in dB’s
In een audiogram vergelijken we de gehoordrempel van een slechthorende met de gemiddelde
gehoordrempel van goedhorenden.
De schaalverdeling van een audiogram is logaritmisch voor wat betreft de frequentieschaal
De schaalverdeling in dB’s is eigenlijk ook logaritmisch, omdat de dB zelf al logaritmisch is
De gehanteerde dB’s bij toonaudiometrie zijn dB’s Hearing Level (HL)
18